【2017年前期・千葉県公立高校入試数学】第5問(タイル並べ・文章題)問題・解答・解説
【はじめに】私は、様々な理由で受験や進学で不利になっている子どもたち(原発被災避難世帯、児童養護施設、母子生活支援施設、ひとり親家庭など)の学習サポートを続けてまいりました。しかし直接伺える場所・教えられる子どもの数は限られますので、どなたでもご覧いただけるように、公式サイトにその内容をUPすることにいたしました。どうぞご活用ください。
【注意事項】
①前半に問題、後半に解答解説があります。問題にじっくりとりくみ考えたい人は、「以下解答解説です」の画像のところで画面を止める(印刷した場合はそれより下を見ない)ようにしてください。
②入試問題は実際は、白黒です。ただせっかくの画像上ですので、カラーをつけました。
【千葉県公立高校入試】前期数学第5問(問題・15点)
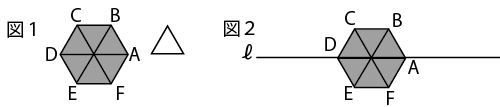
下の図1のように、1辺の長さが1㎝の正六角形ABCDEFのタイルと、1辺の長さが1㎝の正三角形のタイルがある。正六角形のタイルは1枚、 正三角形のタイルはたくさんある。下の図2のように、 正六角形の2つの頂点A、Dを通る直線をℓとする。
次のルールに従って、正六角形のタイルの周りを囲むように正三角形のタイルを順に1枚ずつ、すき間なく置いていき、1辺の長さが1㎝ずつ長くなる正六角形を作っていく。ただし、タイルの厚さは考えないものとする。
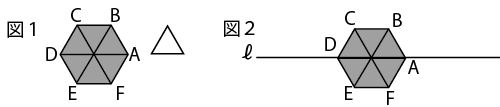
ルール 1 正三角形のタイルの1辺を直線ℓ上に置き、正六角形と正三角形のタイルの頂点が重なるようにする。
2 反時計回りに、正三角形のタイルを1枚ずつ正六角形になるまで置いていく。
3 1、2を繰り返す。
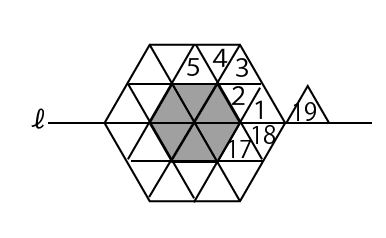
例えば、図3はルールに従って、1辺の長さが2cmの正六角形を作った後、19枚目の正三角形のタイルを直線ℓ上に置いた状態である。
次の(1)~(3)の問いに答えなさい。
(1)1辺の長さが3cmの正六角形を作ったとき、使った正三角形のタイルは全部で何枚になるか、求めなさい。(3点)
(2)ある正六角形を作ったとき、使った正三角形のタイルは全部で144枚であった。このとき、正六角形の1辺の長さは何cmになるか、求めなさい。(4点)
(3)正三角形のタイル1枚に1色ずつ、赤、緑、青の色を塗る。「赤→緑→緑→青→青→青」の順にくり返し、ルールに従って、塗られたタイルを置くこととする。下の図4は、1辺の長さが2cmの正六角形を作った後、19枚目の正三角形のタイルを直線ℓ上に置いた状態である。次の①、②に答えなさい。
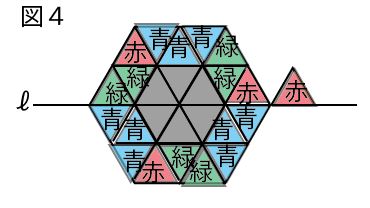
①1辺の長さが8cmの正六角形を作ったとき、使った緑色の正三角形のタイルは全部で何枚になるか。求めなさい。(4点)
②赤、緑、青の色に塗られた正三角形のタイルが、それぞれ400枚ずつあるとき、タイルを使ってできる最も大きい正六角形の1辺の長さは何cmになるか。求めなさい。(4点)

【解答】(計15点)(1)48枚(3点) (2)5cm(4点) (3)①126枚(4点)②11cm(4点)
【動画解説(10分)】以下の文章の解説内容を動画でも配信しています。ぜひ合わせてご覧ください)
10分動画(2017年前期・千葉県公立高校前期入試第5問解答解説)
【解説】
(1)1辺の長さが3cmの正六角形を作ったとき、使った正三角形のタイルは全部で何枚になるか、求めなさい。(3点)
このまま考えてもわからないので、わかりやすい区画に分割して考える。正六角形を対角線で6分割した区画で考える。すると1区画のタイルは正三角形型に規則的に並ぶことがわかる。
まず2周目までタイルを敷きつめ、1辺が2cmの正六角形(1区画では1辺が2cmの正三角形)を作るところまで考えると、以下のようにタイルの数は18枚(3枚×6区画)が必要である。
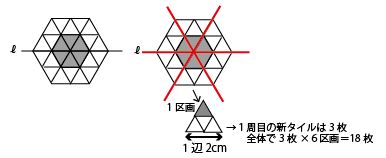
同様に3周目までタイルを敷きつめ、1辺が3cmの正六角形(1区画では1辺が3cmの正三角形)を作るところまで考えると、3周目に使ったタイルの数は30枚(5枚×6区画)が必要である。
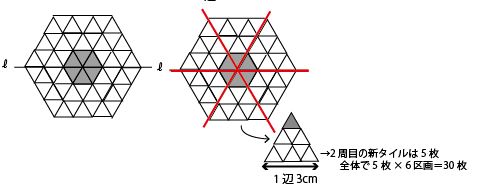
全部で18枚+30枚=48枚必要となる。
(2)ある正六角形を作ったとき、使った正三角形のタイルは全部で144枚であった。このとき、正六角形の1辺の長さは何cmになるか、求めなさい。(4点)
144枚÷6区画=24枚。つまり1区画に24枚タイルを敷きつけた正三角形を作った時、1辺の長さ何cmの正三角形ができるかを求めればよい。
区画にタイルを何周も敷きつめた時のタイル数は以下のようになる。

1周目3枚、2周目5枚の後の各周の新らしいタイル数は、7、9、11と2枚ずつ増えることが予測できる。

周目数に1を足したものが正三角形の1辺の長さになる点に注意してください。
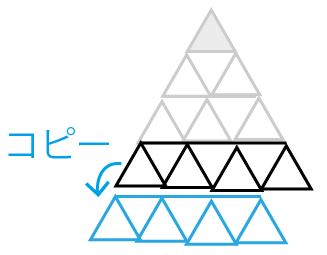
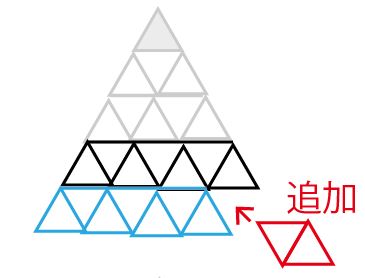
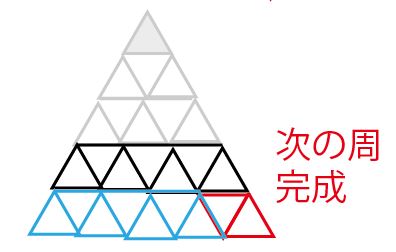
1周増えるごとに新しく敷きつめるタイルの数は2枚ずつ増えていくことは以下の図のように説明できる。
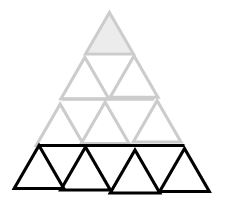
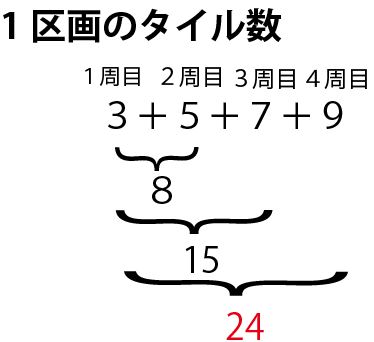
1区画24枚となるのは、以下の計算から4周目まで、つまり1辺5cmであることがわかる。
(3)正三角形のタイル1枚に1色ずつ、赤、緑、青の色を塗る。「赤→緑→緑→青→青→青」の順にくり返し、ルールに従って、塗られたタイルを置くこととする。下の図4は、1辺の長さが2cmの正六角形を作った後、19枚目の正三角形のタイルを直線ℓ上に置いた状態である。次の①、②に答えなさい。

①1辺の長さが8cmの正六角形を作ったとき、使った緑色の正三角形のタイルは全部で何枚になるか。求めなさい。(4点)
6枚単位で繰り返し色タイルを置くことになるので、各色のタイルの枚数の全体の中での比率は赤タイル:緑タイル:青タイル=1/6 :2/6(1/3) : 3/6(1/2)。
8㎝なので7周タイルを敷き詰めることになる。1区画の枚数は以下のように63枚となる。

6区画分の1/3、つまり2区画分が、緑タイルとなる。63×2=126枚。
②赤、緑、青の色に塗られた正三角形のタイルが、それぞれ400枚ずつあるとき、タイルを使ってできる最も大きい正六角形の1辺の長さは何cmになるか。求めなさい。(4点)
青タイルが最も多く使われるので、青タイルが最初になくなり、それ以上の正六角形は作れなくなる。青タイルの比率は全6区画の1/2なので3区画分。
1区画分で考えると400/3 =133.33…枚(133枚)までは使うことができる。

10周目までは敷きつめることができるが11周目までは敷きつめることができない。よって10周目、11cmの正六角形となる。