2022年大学入試共通テスト数ⅠA第1問[1](配点10点)問題・解答・解説
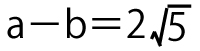
2022年9月 予備校講師・船橋市議 朝倉幹晴
2022年大学入試共通テスト数ⅠA第1問[1](配点10点)の解答・解説を作成しました。勉強・入試対策にご活用ください。問題の末尾をクリックすると解答・解説ページに飛びます。
2022年大学入試共通テスト数ⅠA第1問[1](配点10点)
[1]実数a、b、cが
a+b+c=1・・・・・![]()
および
a2+b2+c2=13・・・・・![]()
を満たしているとする。
(1)(a+b+c)2を展開した式において、![]() と
と![]() を用いると
を用いると
ab+bc+ca=アイ(2点)
であることがわかる。よって
(a-b)2+(b−c)2+(c-a)2=ウエ(2点)
である。
(2)![]() の場合に、(a-b)(b−c)(c-a)の値を求めてみよう。
の場合に、(a-b)(b−c)(c-a)の値を求めてみよう。
b−c=x、c-a=yとおくと
![]()
である。また、(1)の計算から
x2+y2=キク(2点)
が成り立つ。
これらより
![]()
である。
[next_p]