2020年前期、千葉県公立高校入試「数学」第4問「図形の証明」(配点15点)問題・解答・解説(動画と文字両方あり)

まず千葉県の「図形の証明」問題の流れを把握しよう。
もしかしたら、2021年の一本化の影響で変化が出る可能性もありますが、10年来続けてきた証明問題の以下の流れは変わらないと見ておいたほうがよいでしょう。以下がこの10年来の出題の流れです。

2020年前期の問題をこの流れにあてはめて考えると以下のようになります。

★正答率から見た昨年度までの第4問へのアプローチと、今年度からの変化
さて、正答率を見てみましょう。例年同じ傾向ですが、記号記入の(1)(a)(2点)が97.6%、(1)(b)(2点)が68.6%。ここまではできてほしい問題です。
しかしながら、証明記述(1)(c)(6点)では、6点満点が11.0%、部分点(3点)が5.4%です。つまり0点の人が83.6%です。更に(2)にいたっては正答率0.2%、つまり500人に1人のみができ、499人はできない問題ということになります。
そこで、数学が得意ではない中学生には、
『「図形の証明」第4問の(1)(a) (b)(記号選択)は必ず答えてほしい。ただ。(1)(c)(証明記述)と(2)(計算)は正答率が低いので、他の問題の間違いがないかの見直しをまず重視し、その上で時間が余った時に挑戦してください。』
と前置きした上で、解き方を教えてきました。しかし、もちろん第4問も解けたほうが得点をUPできます。だから、ぜひ、この解答例をしっかり演習し、最初からあきらめることなく「図形の証明」にも挑戦するように努力してみてください。(本番でどうしても時間がなくなってしまった場合は、これまで通り、他の問題優先で仕方ないと思います。)
★千葉県前期第4問「図形の証明」添付図の数の変遷とその活用
2012年は、「図形の証明」に添付された図は1つのみであったものが、2013年から2つとなり、2015年からは3つとなり、現在にいたっています。
毎年、問題自体の難易度が若干変化するので、一概に比較できませんが、図1つだった2012年度は6点は4,4%、3点は3,5%で合わせて7.9%だった正答率が、図2つにした2013年度は6点が8.7%、、3点が4.6%で合わせて13.3%に上昇しました。
つまり、「手段の証明」と「目的の証明」の2段階となっている千葉県の問題を1つの図だけで考えさせるのは無理であると、出題者(千葉県教育委員会)がようやく気付き、図を多く添付するようになったのです。だから、受験生側は、3つの図を適切に使い分けで活用する必要があります。
3つの図のうち最後の図は(2)に添付されているので、(2)計算問題用です。したがって、(1)「図形の証明」部分では最初の2つをうまく使いわける必要があります。
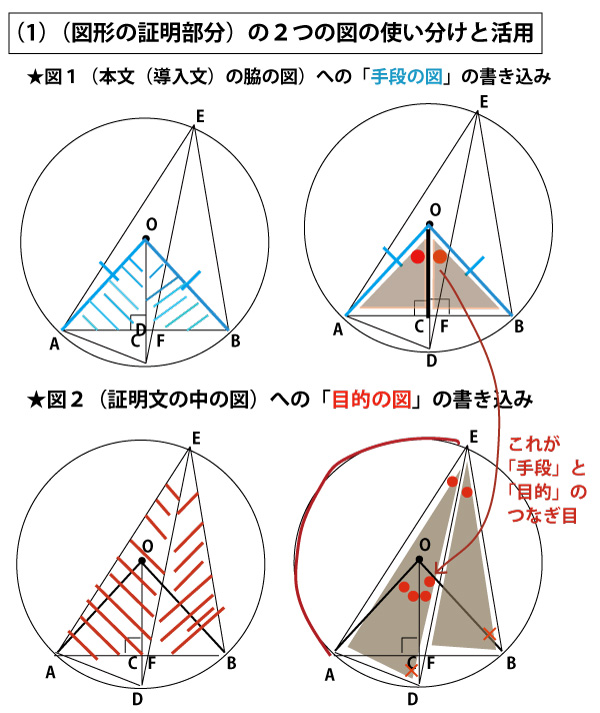
★(1)(図形の証明部分)の2つの図の使い分けと活用
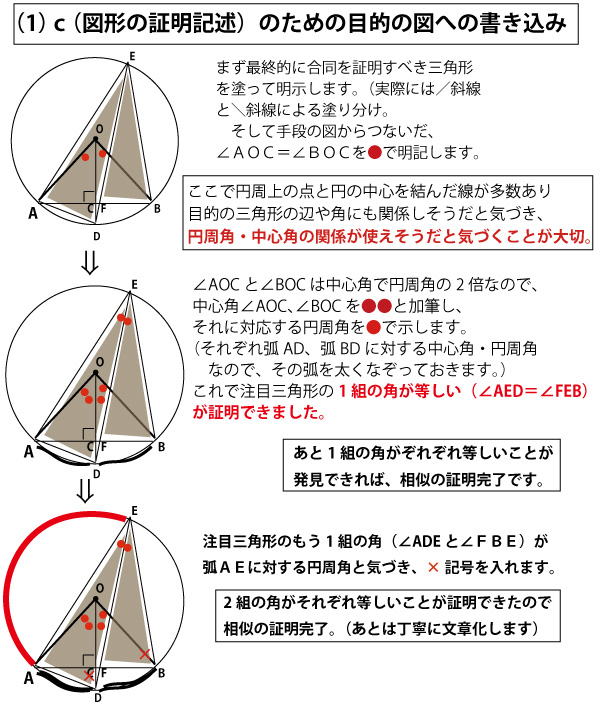
本説明では、これまで、前半、手段の図の証明までの流れを青、後半、目的の図の証明を赤で説明してきました。その色分けをそのまま活用して説明します。
下図のように使い分けることをお勧めします。簡単にいうと、図1(最初の図)を「手段」の書き込み、図2(証明文の中の図)を「目的」の書き込みにし、混同しないように使いわけるのです。
実際、試験の時は、色は使えず、すべて「黒鉛筆」のみで書き込みをして考えなければなりません。まず図1に手段で注目する2つの三角形に写真を引き、その三角形の合同を証明するという目的を明記します。そして「合同条件」に相当するものを、線の長さが等しいことを示す「|」の書き込みや、角度(この場合直角)の書き込みなどをしていくわけです。本図では三角形を斜線で塗った状態を左、角度や線の書き込みをしたものを右にかき分けていますが本当はそれぞれ1つの図になります。
(説明のための赤・青の斜線の角度記号の●×が重なって見えにくいため2つに分離し、右図では写真を塗りつぶしで表現しています。試験の時は塗りつぶしは時間がかかるので斜線(2図の違いが分かるように、/図形と、\図形の書き分け)をお勧めします。
1図の手段の証明の中に1つだけ赤●の部分があります。ここが手段の結果が後半の目的の図の証明のつなぎ目になることを示しています。
図の使い分けの発想をご理解いただいた上で、以下、実際にこの問題を解いていきましょう。
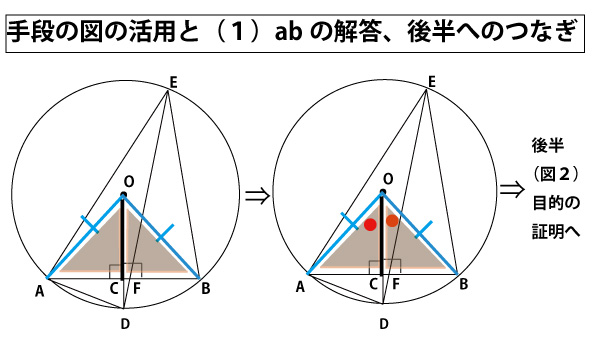
★手段の図活用と(1)abの解答、後半(目的)へのつなぎ
前半(手段)で証明すべき2図を塗ります(実際の試験では/斜線と\斜線による描き分け)。すると出題者が(a)(b)に関して問うている流れがわかりやすくなります。
円の半径であるから、OA=OB(aの答、ウ)
(出題者は「円の半径」という言葉だけで気づかせないようにわざと図1にはOA、OBの線を書きこんでませんが、自ら書き込みます。)
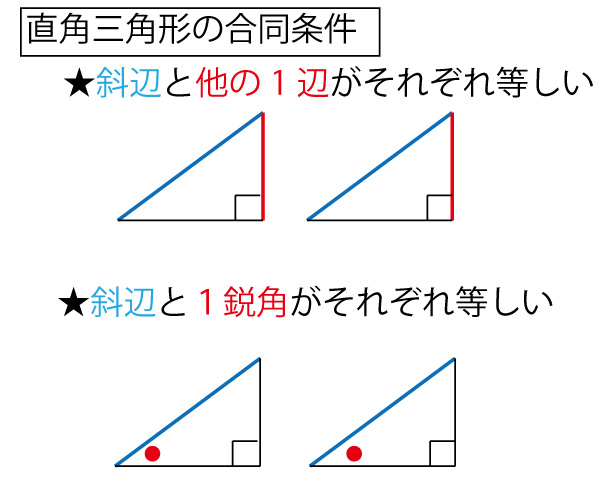
2つの三角形が直角三角形であることと、普通の三角形の合同条件に比べ、角や辺の長さの情報が少ないことから「直角三角形の合同条件」が使われていると類推でき、図より「直角三角形の斜線と他の1辺」(bの答、カ)だということがわかります。
この2つの直角三角形の合同の証明は、手段であり、次の目的の証明(証明の記述部分)のためにそれを活用します。そのつなぎ目を見つけることが大切です。
三角形は、3辺・3角があり、そのうち3つを組み合わせると合同が証明できます。合同が証明されると、未知であった、残りの3つ(この場合AC=BC、∠AOC=∠BOC、∠OAC=∠OBC)がそれぞれ等しいことがわかります。その3つのどれかが、次の目的の証明の出発に活用できるのです。1つのクイズを解いた解答に中に次のクイズの解き方のヒントが入っている連続クイズのようなものです。
最終目的は三角形の相似の証明です。相似の証明には「2つの角がそれぞれ等しい」ことを使うことが多いので、∠AOC=∠BOC、∠OAC=∠OBCのどちらかを使うことが類推できます。∠AOCと∠BOCが中心角であり、図にはばっちり円が描かれているし、円周角・中心角の定理の活用につなげられると予測できれば、∠AOC=∠BOCが次の証明のつなぎと予測できます。
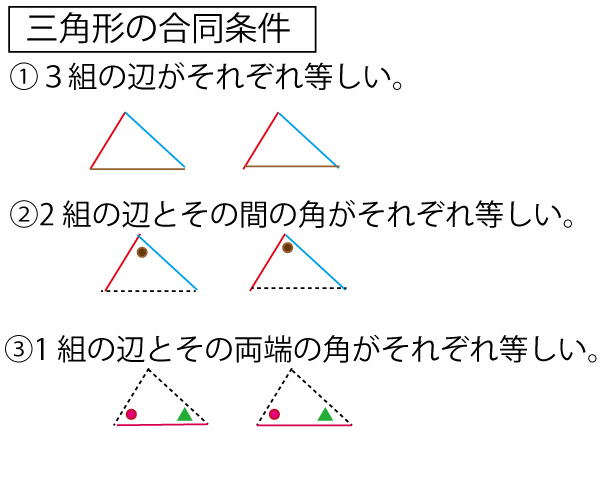
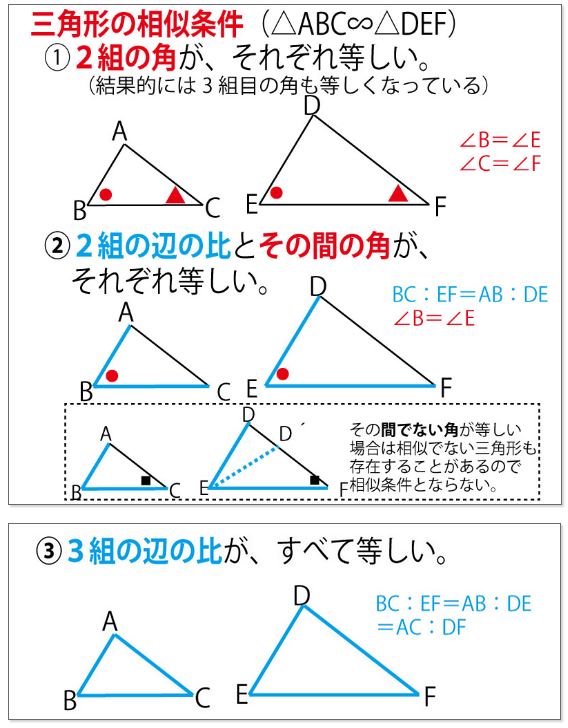
三角形の相似条件を確認しましょう。
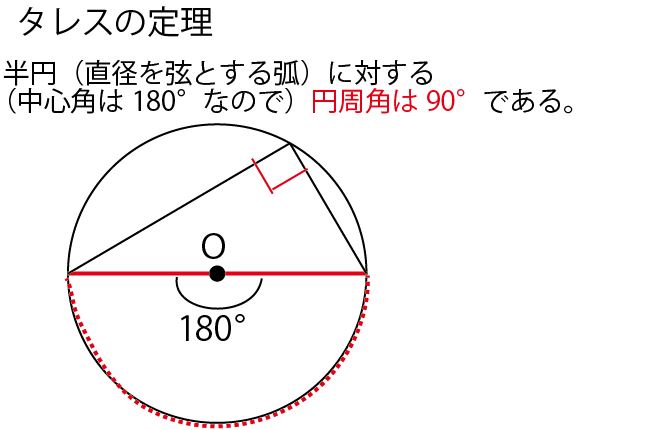
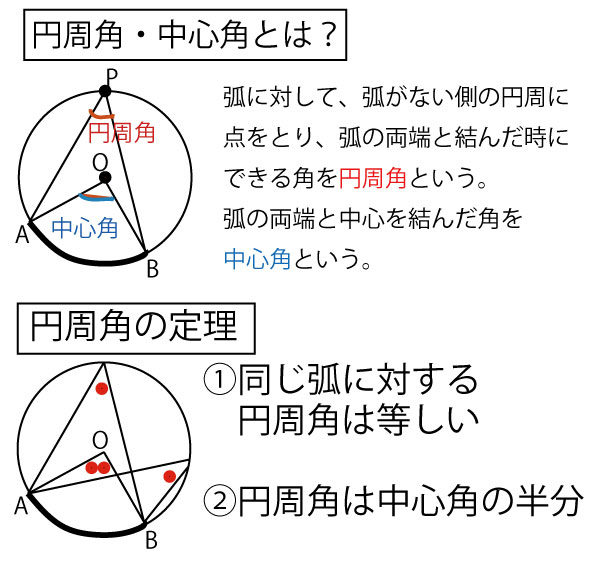
円周角の定理を確認しましょう。
以上を文章にまとめると、以下のようになる。ただし内容が合っていればよいので、文章表現が少し異なってもかまわない。
(2)解説
正答率0.2%の問題です。昨年の中3の500人に1人、1つの中学校に100~200人の中3がいたとしても、3つの学校で1人しか解けなかった問題です。自力で解けるとは思わすに、この思考過程をたどることで、いろいろな図形の計算の発想に慣れ、2021年度以降、問題がもう少し簡単になった時には解けるようにしましょう。
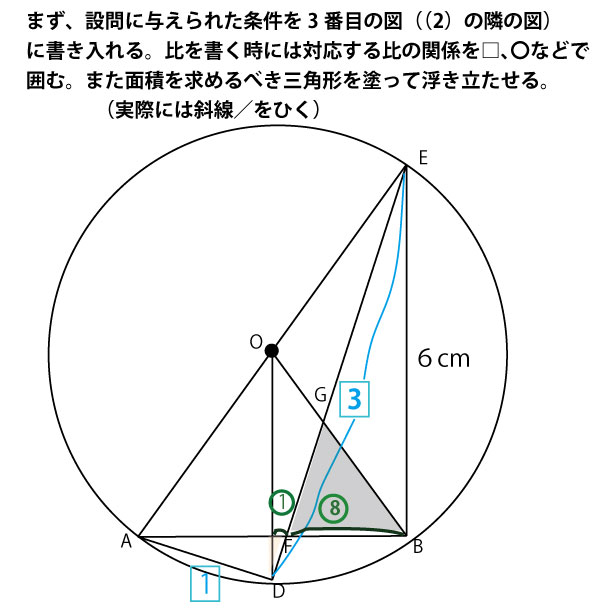
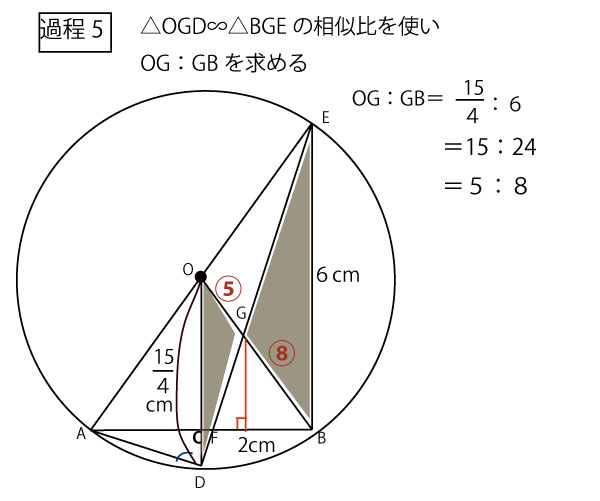
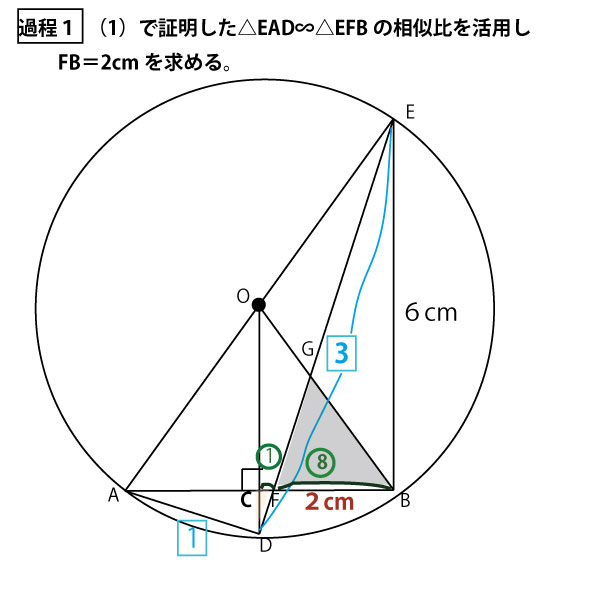
★過程1(底辺FBの長さを求める)
数学の問題は、前問で使った結果を次の問題で使うことが多い。千葉県でも(1)の図形の証明で召命した結果を(2)の計算で使うことが多い。
(1)で証明した△EAD∽△EFBを使えるのではないか?特に相似図形なので相似比を使えるのではないかと考えてみる。三角形の相似比でEB:BF=ED:DA=3:1。EB=6cmなので、6cm:BF=3:1、 3BF=6cm BF=2cmとわかる。すると目的三角形の底辺の長さがわかったので、次に高さを求める方向を考える。
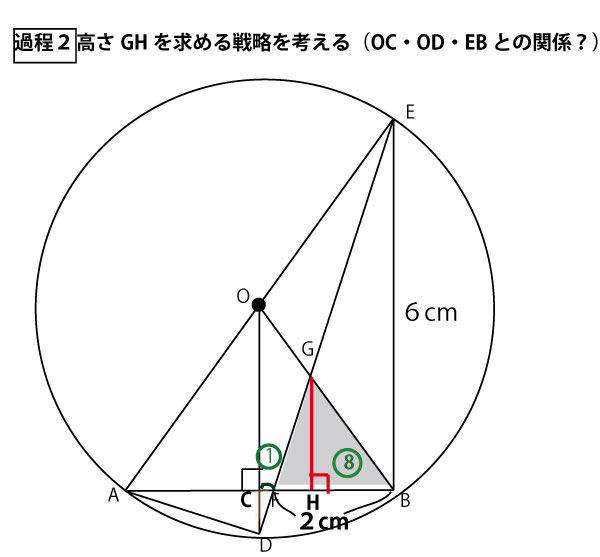
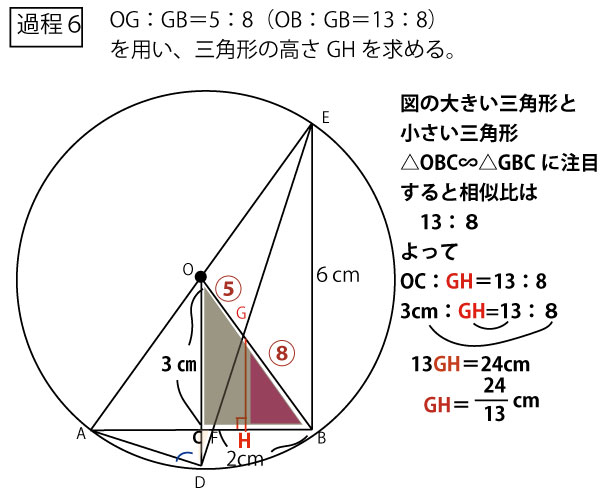
★過程2 高さGHを求める戦略を考える。(OC・OD・EBとの関係?)
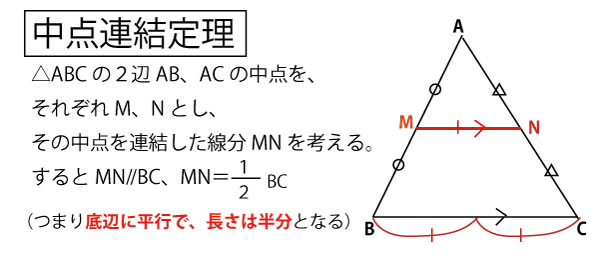
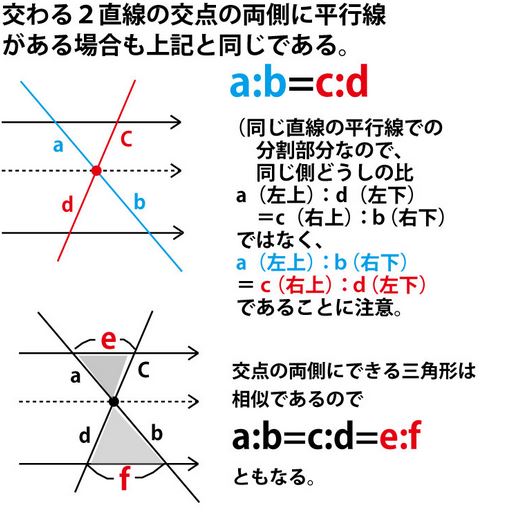
Gから底辺FBに垂線をおろし、FBとの交点をHとして描く、GHの長さが三角形の高さであり、これを求めればよいが簡単そうではない。描いてみると、GHの両脇にOC、ODとBFが同じように垂直に立っている(厳密にはEBが垂直かどうかはまだ証明されていない)。この長さとの関係を使っていくと予測し、「タレスの定理」「中点連結定理」「平行線と線分比」など図形に関する定理を総動員して考える。
★これから使う3つの定理
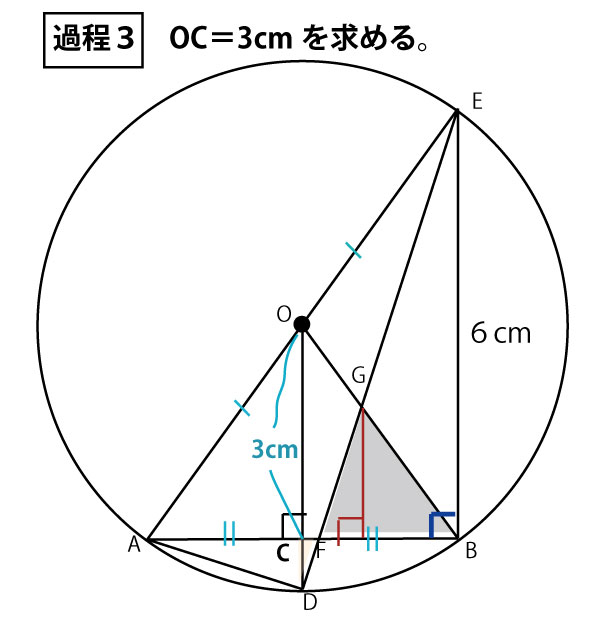
★過程3 タレスの定理・中点連結定理を用い、OC=3cmを求める
△ABEに注目する。AEが直径なので「タレスの定理」より、∠ABE=90°。AB⊥BF。またOからABに下ろした垂線がODなので、OD∥EB。OはAEの中点(直径は中心で二等分あれる)、また前問よりAC=BCでCはABの中点なので、△ABEに対する中点連結定理より、OC=1/2EB=1/2 ×6cm=3cm。
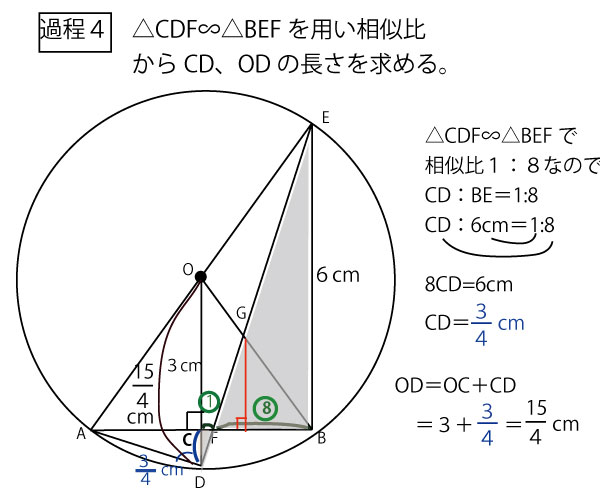
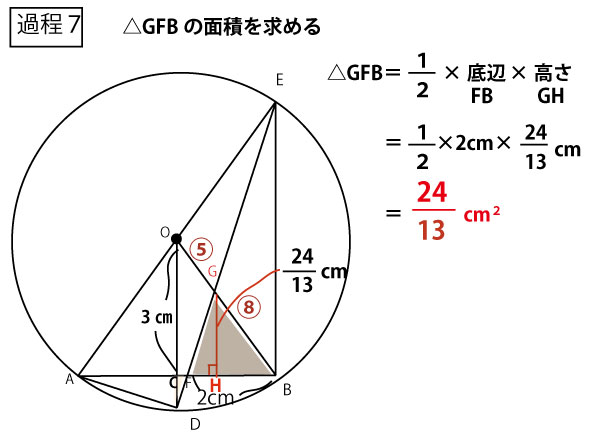
★過程4 相似比(平行線と線分比)を使って、CD(OD)の長さを求める。