2020年前期、千葉県公立高校入試「数学」第5問（総合問題）問題・解答・解説（動画と文字両方あり）

2020年10月12日 2020年10月13日

asakura

【解答（第5問）】（2020年前期・千葉県）（配点15点）

（1）450（個）（配点3点）（正答率72.6%（無答率2.0%))
（2）４（個）（配点3点）（正答率42.0%（無答率22.3%))
（3）箱Aを2回、箱Bを1回、箱Xを2回使って増やすので、個数は１×３²×5×x²個となり、これが540ｘ個となるので、
　　１×３²×5×x²＝540ｘ　　これを解いていくと　45x²＝540ｘ　ｘ²＝12x　x²−12x＝0 x(x－12)＝0
　　ｘ＝０,12が解となる。ｘは自然数なので　ｘ＝12（配点4点）（12.4％が4点、10.6％が2点（無答率50.8%))
（4）５／16（配点5点）（正答率17.5%（無答率38.3%))

【解説】

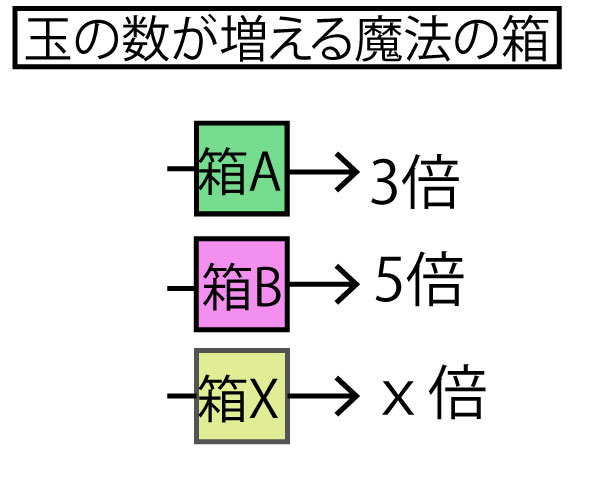
箱Aを通すと３倍になるから、箱Aは「×３」、箱Bを通すと5倍になるから箱Bは「×５」、箱Xは「×x（かけるエックス）」の計算を示す。

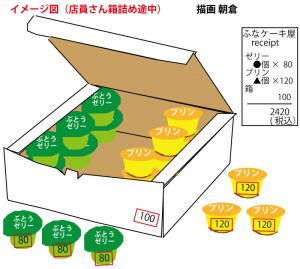
（1）２AABBなので、２×３×３×５×５＝450個
（2）AとBを合わせて5回使ったのであるが、それぞれ何回ずつかはわからない。AAAABかもしれないし、BBABAかもしれない。ただABは順番が変わっても結果は同じなので、ABの回数だけが問題である。最初の数をaとすると
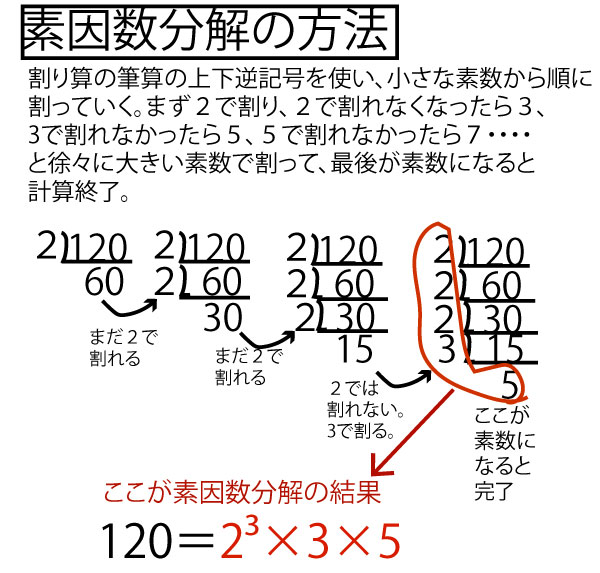
a×３か５を5回かける＝2700なので、2700が、３や５や他の数をどうかけるとできるのかを考える。３も５も素数であるので、2700の中にどのような素因数（素数の約数）が含まれているかを調べれる素因数分解をすればよい。

整数に関する用語の整理
★因数（いんすう）　正の整数（自然数）がいくつかの自然数の積で表されるとき、その１つ１つをもとの数の因数という。約数と同じである。
例　30＝１×30　30＝２×15　30＝３×10　30＝５×６　30＝２×３×５
　　　　よって、1，30、２、15、３、10、５、６は30の因数である。
★素数（そすう）
１とそれ自身以外に因数（約数）を持たない２以上の自然数。（１は素数に含めない）
２、３、５、７、11、13、17、19、23、29、31・・・・・（2以外は全て奇数）
★素因数分解　素数である因数を素因数といい、自然数を素数の積で表すことを素因数分解という。
30＝２×３×５
120＝２×２×２×３×５＝2³×3×5
(ある数をｎ回かけることは「ｎ乗」といい、数の右肩に小さくかけた回数を記す。２³は「２×２×２」、２の３乗を示す）

この設問で2700個となるかけ算を分析するため、素因数分解をしてみる。

すると箱Aが3回、箱Bが2回で計5回操作であり、最初の数が4個であったとわかる。

（3）箱Aを2回、箱Bを1回、箱Xを2回使って増やすので、個数は１×３²×5×x²個となり、これが540ｘ個となるので、
　　１×３²×5×x²＝540ｘ　　これを解いていくと　45x²＝540ｘ　ｘ²＝12x　x²−12x＝0 x(x－12)＝0
　　ｘ＝０,12が解となる。ｘは自然数なので　ｘ＝12
（これは解答がそのまま解説である。若干文章表現が違っても内容が合っていれば正解となる。部分点2点はおそらく０を除外しなかった場合などと思われる）

（4）最初４個から始め、AとBの操作を計4回したものが、「1000個を越え」ればよい。1000個ぴったりでは「1000個を超え」たことにならないので、実際は1001個以上、４の倍数だから1004個以上であることが必要である。
つまり最初から、251倍以上になっていればよい。
Aの操作とBの操作を合計4回で、AとBは順番は関係なく、それぞれの回数がかけ算の数を決めるので、Aを先に書くと
AAAA
AAAB
AABB
ABBB
BBBB

の５通りがありうる。
それぞれの掛け算は
AAAA＝３×３×３×３＝81倍
AAAB＝３×３×3×５＝135倍
AABB＝３×３×５×５＝225倍
ABBB＝３×５×５×５＝425倍
BBBB＝５×５×５×５＝625倍

であり、最後の２つの場合のみが251倍以上となる。

ここまでは、それぞれの箱の回数だけで考えたが、コインの表裏で表ならA、裏ならBを選ぶ。「表」と「裏」という漢字は一見して区別しにくいので、表を〇、裏を×と表記する。
ので、表裏（〇×）の出方は
1回目について「〇か×」の２通り
2回目についても「〇か×」の２通り
３回目についても「〇か×」の２通り
４回目についても「〇か×」の２通り

なので２×２×２×２＝16通りの出方がある。

このうち、条件を満たす目の出方は
ABBB（〇1回、×3回）となるのは、実際の出方の順番まで考えると

〇×××（ABBB）、×〇××（BABB）、××〇×（BBAB）、×××〇（BBBA）の４通りとなる。

BBBB（×4回）となるのは、XXXXの１通りのみである。
すると計5通りなので、５／16となる。