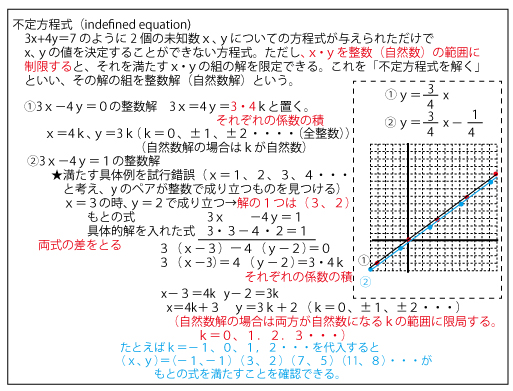
2021年大学入試共通テスト「数学IA」第4問「整数論」（配点20点・選択）問題・解答・解説

2021年2月13日 2022年2月7日

asakura

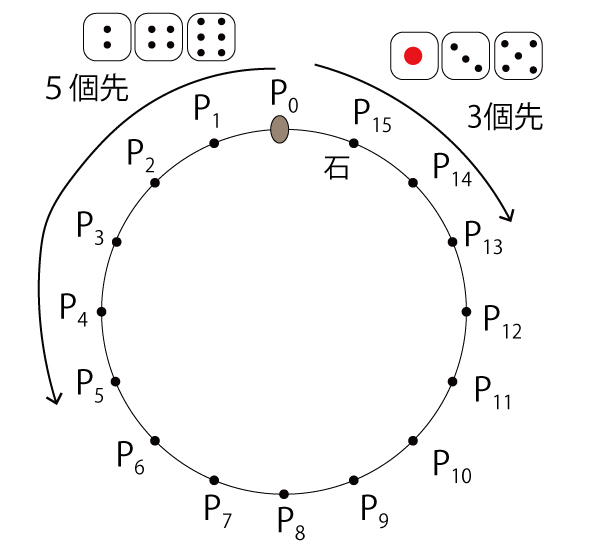
解説

（1）

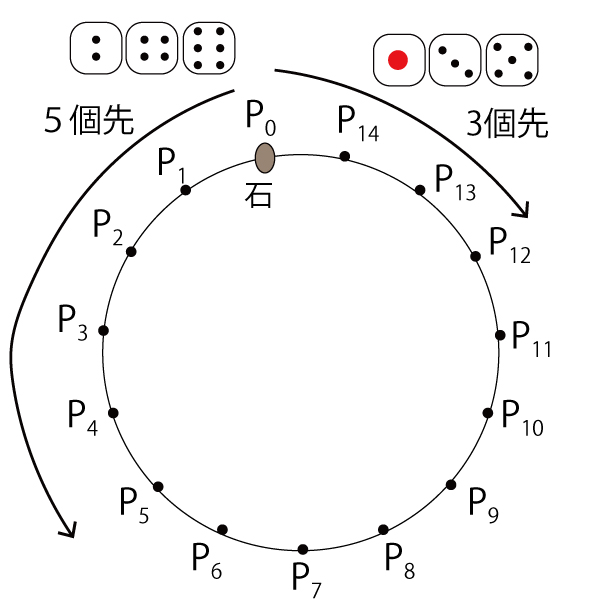
Pの番号の数字で考えてみる。その１個先に移動することを距離１とみなし、Pの番号が増える「反時計回り」を＋、Pの番号が減る「時計回り」を－とする。偶数の目が出ると数は＋５で、奇数の目が出る時は－３である。偶数の目がｘ回、奇数の目がｙ回出るとすると移動距離は5x－3yとなる。
ただし＋15で反時計回りに1回転するため、＋15は０に戻る。
同様に－15で時計回りに1回転するため、－15は０に戻る。

移動数に「出る順番」は関係なく「偶数の目・奇数の目の回数」のみが関係する。
合計で5回ふっているのでｘ＋ｙ＝５となる。
だから、次の連立方程式を解けばよい。
5x－3y＝１・・・
ｘ＋ｙ＝５・・・

よりｙ＝５－ｘ。これをに代入。
5x－３（５－ｘ)=1
5x－15＋3x＝１
8x＝16
ｘ＝２（ア、1点）、ｙ＝３（イ、1点）

（ちなみに5x－3y＝－14の可能性を考えてみると
5x－3（5－x)＝－14
5x －15＋3x＝－14
8x＝１　でｘ＝１／８となり、回数としては成り立たない。
同様に5x－3y＝16の可能性を考えてみると
5x－3（5－x)＝16
5x －15＋3x＝16
8x＝31　ｘ＝31／８となり、これも「回数」としては成り立たない。
厳密にはここまでの確認も必要であるが、最初の＝１で的確な答が出ているので、それで答えてよいだろう。
時間に余裕があれば確認してください。）

なお、連立方程式が思いつかない場合でも、わずか6通りなので実際に入れて確認してもよい。
回数の組としては以下の６通りがありうる。
１、偶数5回、奇数0回
＝＋５×5＝＋25＝＋15＋10＝10
２、偶数4回、奇数1回
＋５×4－３＝＋20－３＝+17＝＋15＋2＝０+2＝2
３、偶数3回、奇数2回
＋５×3－３×２＝＋15－６＝9
４、偶数2回、奇数3回
　　＋５×2－３×３＝10－９＝1
５、偶数1回、奇数4回
＋５−３×４＝5－12＝－7＝－15＋8＝8
６、偶数0回、奇数5回
－3×５＝－15＝0

（2）

整数論、不定方程式の一般的考え方は以下のようになる。

この設問においては、問題文の流れにそって、以下のように解く。
問題文の中に「x＝ア×8＋ウk、ｙ＝イ×8＋エk」
と×８があることから（1）で解を求めた＝１の式を8倍して、（2）で求める＝８の式と、連結する発想につなげていく。

5x－3y=８・・・

前問より５×２（ア）−３×３（イ）＝１なので、8倍すると
５×２（ア）×８ー３×３（イ）×８＝８・・・
－より
5x－5×2（ア）×８ー（3y－３×３（イ）×８）＝０
５（ｘ－２（ア）×８）＝３（ｙ－３（イ）×８）＝５・３ｋと置く。
５（ｘ－２（ア）×８）＝５・３ｋで、両辺を５で割ると
ｘ－２（ア）×８＝3k
ｘ＝２（ア）×８＋3k（ウ）

同様に、３（ｙ－３（イ）×８）＝５・３ｋで、両辺を３で割ると
ｙ－３（イ）×８＝５ｋ
ｙ＝３（イ）×８＋5k（エ）（ウ、エ両方できて3点）

ｘ＝3k＋16、ｙ＝5k＋24で、

０≦ｙ＜５（エ）を満たすｋは－４で
ｙ＝５×（－4）＋24＝－20＋24＝４（オ、3点）

このとき

ｘ＝3k＋16＝３×（－4）＋16＝－12＋16＝４（オ、3点）

偶数の目4回、奇数の目4回なので合計8回投げたことになる。（キ、1点）

（3）

最初に述べたように－15は０、＋15は０となるので、
８－15＝－７、あるいは８＋15＝＋23のＰの位置は８となる。
また８－15×２＝８－30＝－23
　　８－15×３＝８ー45＝－37
８＋15×２＝８＋30＝38
８＋15×３＝８＋45＝53
などの場合もPの位置は８となる。

たださいころをふる回数が少ないと移動距離も少ないと考えられるので－７と＋23でまず考えてみる。
5x－3y＝－７
試行錯誤していくとｘ＝１（ク、2点）、ｙ＝４（ケ、2点）で成り立つとわかる。

５×１－３×４＝５－12＝－７
そしてサイコロを振った回数は１＋４＝5回（コ、2点）となりコ（5）＜キ（8）を満たす。
一方、＋23の時は
５ｘ－3y＝23
試行錯誤していくとｘ＝７、ｙ＝４で成り立つとわかる。
５×７－３×４＝35ー12＝23
この時、サイコロを振った回数は７＋４＝11回で、8回（キ）より多いので条件を満たさない。