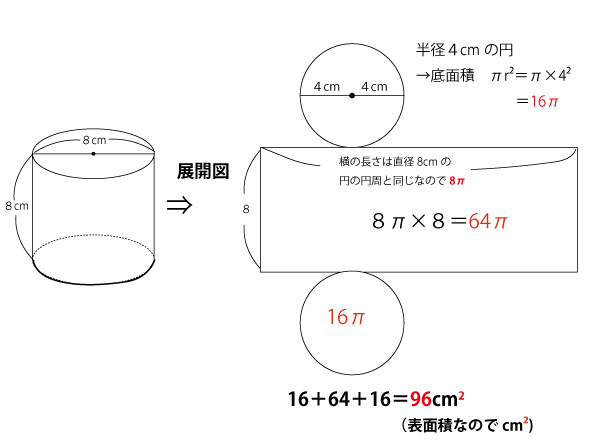
2021年、千葉県公立高校入試「数学」第2問(3)(円柱の体積・表面積)(配点5点)問題・解答・解説
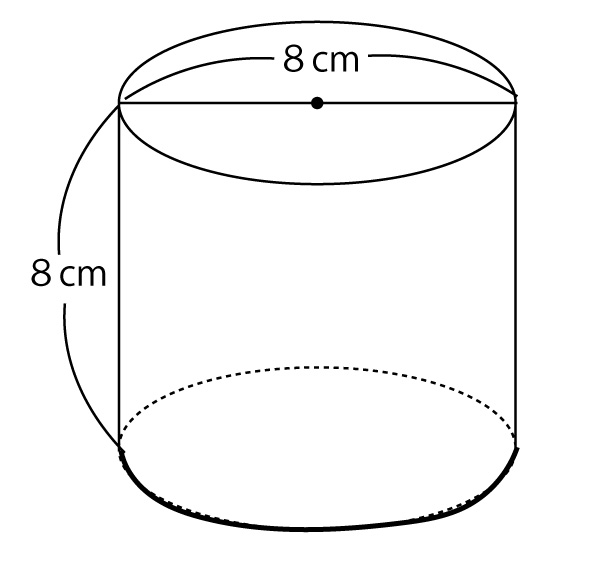
【解答】 cm2 (5点)(正答率52.7%(無答率2.6%))
cm2 (5点)(正答率52.7%(無答率2.6%))
【解説】
まず、設問が「体積」「表面積」のどちらを求める問題なのか確認しよう。
「表面積を求めよ」なのに「体積」を求めてしまうミスが多いので気をつけよう。
体表的な立体の体積と表面積を整理しておこう。。本設問で、「表面積」(底面積・側面積)もよく問われるので、まとめて整理しておこう。
円錐の体積では1/3を掛けることを忘れないようにしよう。
特に円柱と円錐は底面の半径が与えられ、円の面積の公式を使いながら求めさせる形での出題が多いのでとくに整理しておこう。
表面積の場合は側面積と底面積を分離して考えて合計する必要があるし、「側面積」「底面積」単独で聞かれることもあるのでそれぞれ把握しておこう。なお円柱の場合は、日常生活では下(床側)の円を底面(下面)、上側の面を「上面」と区別して表現することがあるが、数学の世界では両方とも「底面積」と表現し、底面が2つあるとみなす。
表面積については上記の計算を公式として暗記しておく必要はない。その都度、展開図を描いて求めればよい。
本設問では以下のようになる。
【参考】立体の体積・表面積の過去問
2020年前期、第2問(3)(三角柱の体積)(5点)
2019年前期、第5問(総合問題、円錐・円柱・球の体積)(計15点)
2018年前期、第2問(3)(三角柱の体積)(5点)第2問(1)(回転体)(5点)
2017年前期、第2問(2)(資料の整理)(5点)
2016年前期、第2問(1)(球の体積・表面積)(5点)
2015年前期、第2問(3)(回転体の体積)(5点)