2019年前期、千葉県公立高校入試「数学」第5問（文章題）解答・解説

2019年2月12日（火）に実施された千葉県公立高校入試の前期試験「数学」の第５問（文章題）（配点15点）の解答・解説です。

試験問題は白黒ですが、画面上ですので一部カラーにし、各小問の配点、そして千葉県教育委員会が発表した正答率・無答率も併記しました。

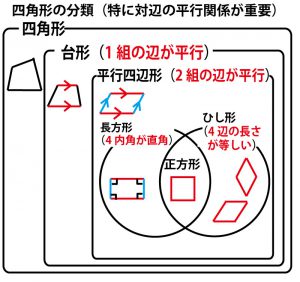
第5問（配点15点）

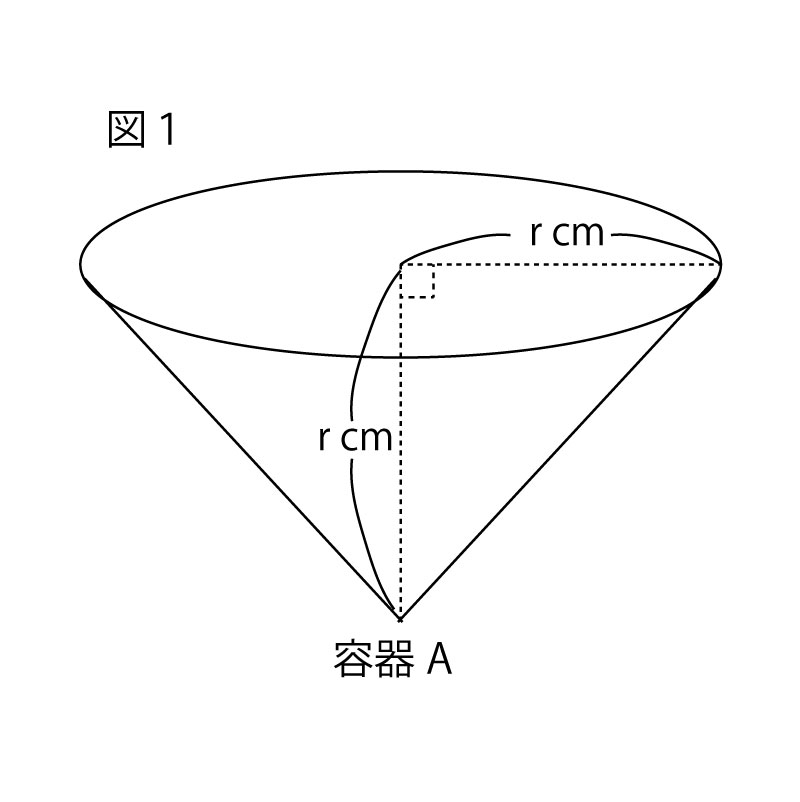
図１のように、底面の半径と高さがともにｒcmの円錐（えんすい）の形をした容器Aがあり、底面が水平になるように置かれている。

このとき、次の（1）～（3）の問いに答えなさい。

ただし、円周率はπ（パイ）を用いることとし、容器の厚さは考えないものとする。

（1）容器Aでｒ＝6cmのとき、次のの問いに答えなさい。

容器Aに水をいっぱいに入れたとき、水の体積を求めなさい。（3点）（正答率63.5%（無答率4.1%))

水がいっぱいに入っている容器Aの中に、半径2cmの球の形をしたおもりを静かに沈めた。このとき、容器Aからあふれ出た水の体積を求めなさい。
　（3点）（正答率33.0%(無答率9.7%))

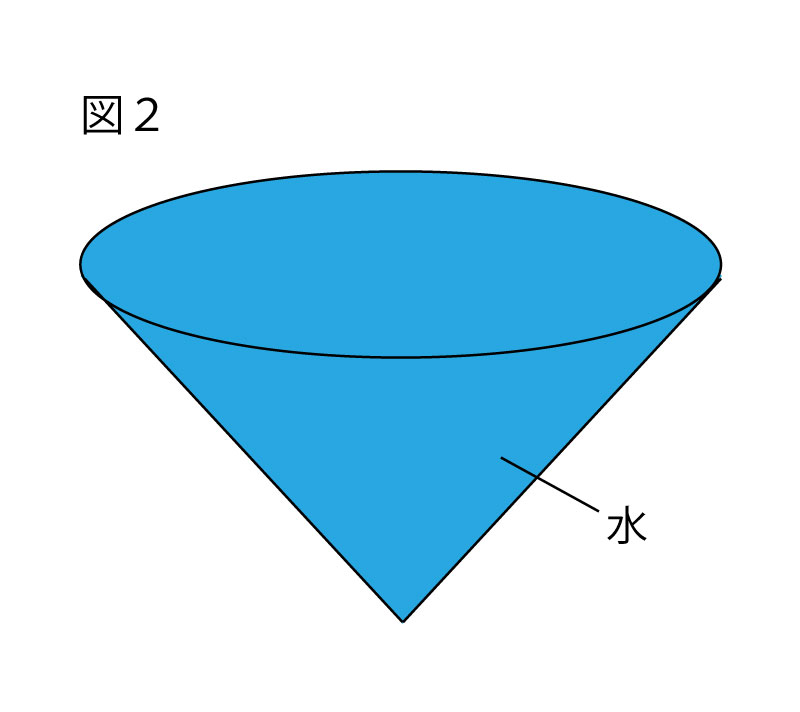
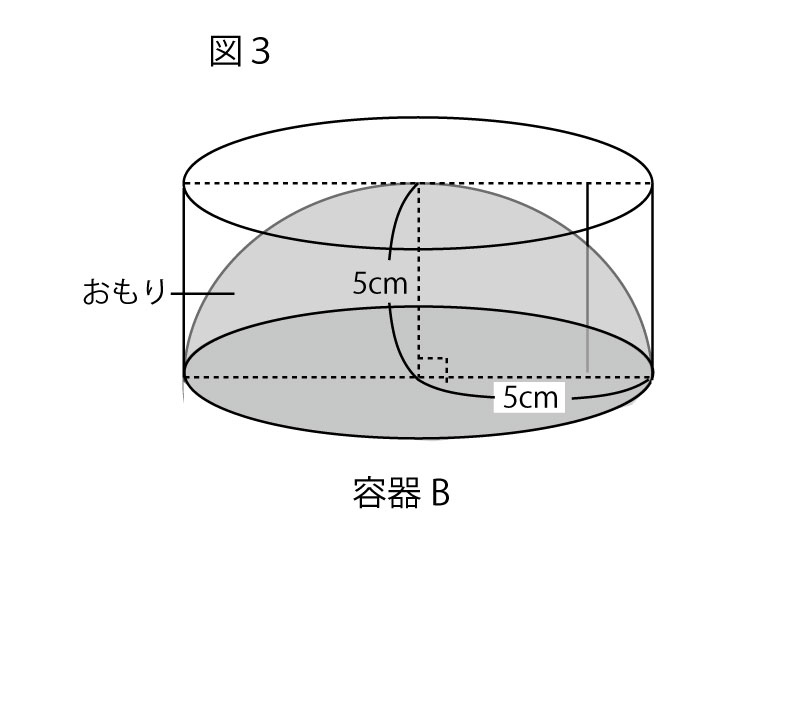
(2)図２は、容器Aでｒ＝5㎝のときに、水をいっぱいに入れたものである。また、図３は、底面の半径と高さがともに5㎝の円柱の形をした容器に、半径5cmの半球の形をしたおもりを入れたものであり、これを容器Bとよぶことにする。容器Aに入っているすべての水を、容器Bに静かに映していく。
このとき、容器Bから水はあふれるか、あふれないかを答えなさい。ただし、その理由を式とことばで書き、答えること。
  (4点）（4点評価18.7%、2点評価6.0%（無答率29.7%))

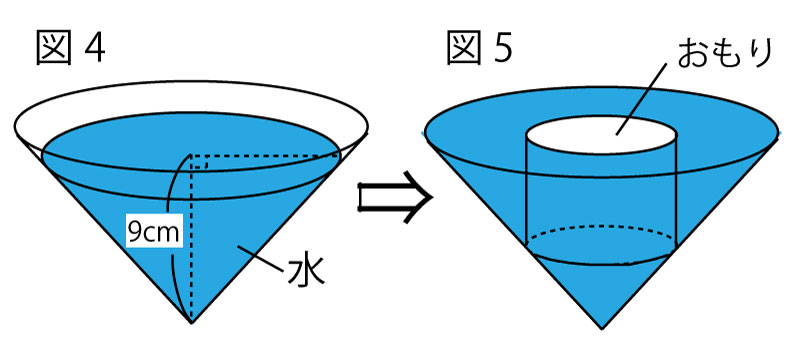
(3)図４は、容器Aでｒ＝10㎝のときに、水面の高さが９cmになるまえ水を入れたものである。その中に底面の半径が４cmの円柱の形をしたおもりを、底面を水平にして静かに沈めると、容器Aから水があふれ出たあと、図５のように円柱の形をしたおもりの底面と水面の高さが等しくなった。このとき、容器Aからあふれ出た水の体積を求めなさい。   (5点）（正答率6.9%（無答率48.8%))

[next_p]