2019年前期、千葉県公立高校入試「数学」第4問（図形の証明）問題・解答・解説

2019年2月12日（火）に実施された千葉県公立高校入試の前期試験「数学」の第4問（図形の証明）（配点15点）の問題・解答・そして私（朝倉幹晴）が作成した解説です。試験問題は白黒ですが、画面上ですので一部カラーにし、各小問の配点、千葉県教育委員会が発表した正答率・無答率も併記しました。

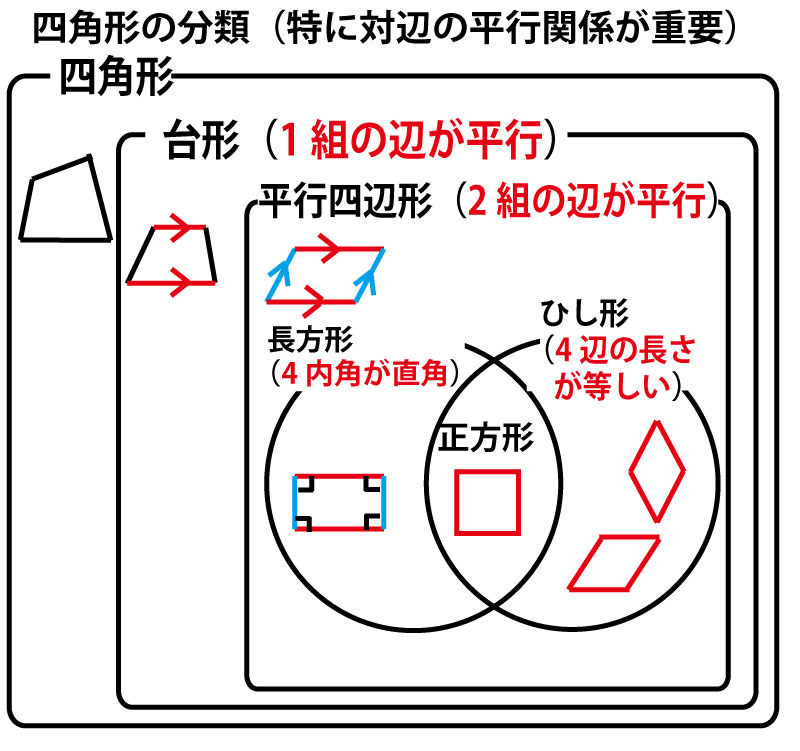
第4問（図形の証明）（計15点）

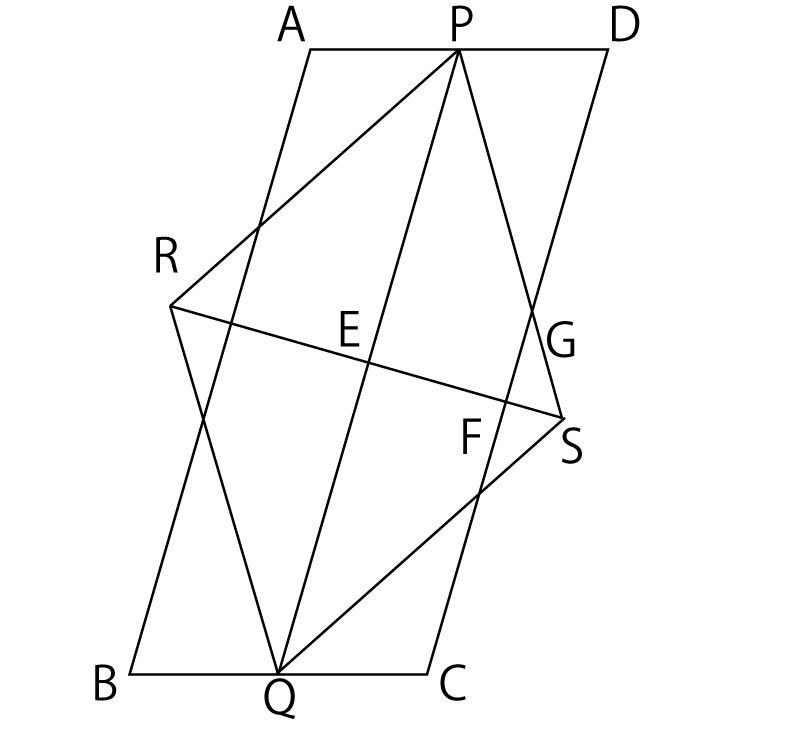
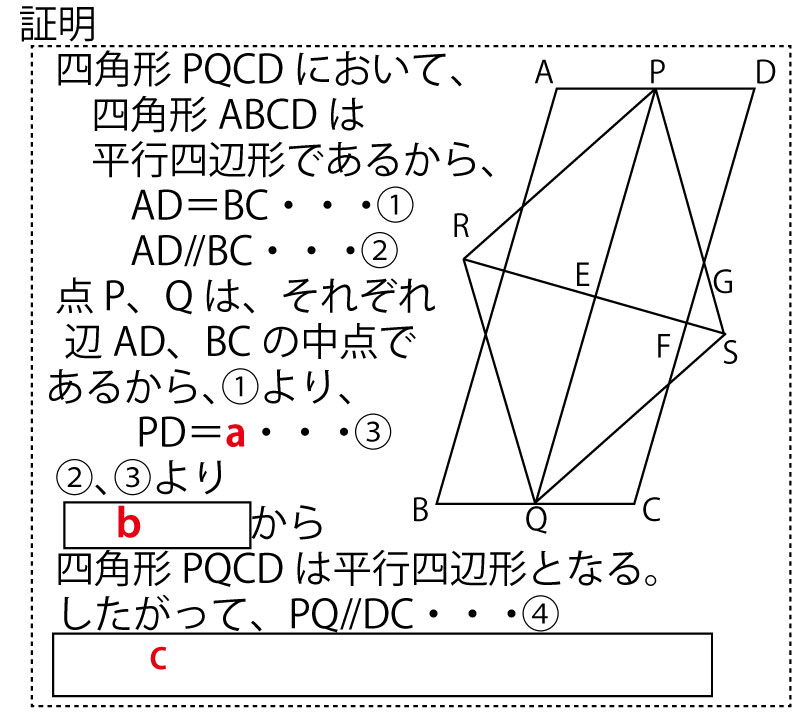
図のように、平行四辺形ABCDがあり、辺AD、BCの中点をそれぞれP、Qとする。2点R、Sを平行四辺形ABCDの外側に、四角形PRQSがひし形になるようにとる。線分PQと線分RSの交点をE、線分RSと辺CDの交点をF、辺CDと辺PSの交点をGとする。このとき、次の（１）、（２）の問いに答えなさい。

選択肢

アPG　イQC　ウES

エ　2組の向かいあう辺が、それぞれ平行である

オ　2組の向かいあう辺が、それぞれ等しい

カ　1組の向かいあう辺が、等しくて平行である

（2）RQ＝5cm、AD=4cm、PG=DG=3cmのとき、線分FSの長さを求めなさい。（5点）（正答率0.2%（無答率35.6%))

[next_p]