2019年前期、千葉県公立高校入試「数学」第4問(図形の証明)問題・解答・解説
解説
千葉県公立高校入試「図形の証明」の問題は、人口が多い7都府県(東京都、神奈川県、埼玉県、千葉県、大阪府、兵庫県、愛知県)の公立高校入試の中で最も難しい。例年、15点配点で、(1)の証明の(a)(2点)(b)(2点)を選択肢から選ばせ、(c)で証明の後半を記述させ(6点)、最後に(2)で(1)の証明結果を使った計算を問う(5点)。
正答率は選択肢を記号で選ばせる(1)(a)(b)は70%以上であるが、(c)(証明記述)と(2)(証明結果をもとにした計算)は正答率は低い(2019年前期では(c)は部分点も含め20%以下、(2)はなんと0.2%)。
したがって、受験生としては、(1)(c)と(2)(計11点)はあきらめ、(a)(b)(計4点)だけを正確に答え、考える時間・検算する時間を他の問題に振り向けたほうがよい。
とはいっても、(a)(b)を確実に正解にするためにも、また可能ならば(c)や(2)を最初からあきらめるのでなく、他の問題を解いた上で、残った時間で、最後に(c)や(2)に戻り、得点できればまでできれば、うれしい。そこで以下のように、千葉県独特の問題の構成と発想をあらかじめ理解しておけば、(c)(2)も解くことができる(cで6点でなくても部分点3点を得ることができる)可能性があるので、しっかり理解しておこう。
このように証明の前半(この中に(a)(b)もあり)で手段を示し、その結果を使い、本文の冒頭に書いてある目的を証明させるという構成になっている。
(c)部分を解くためには目的にいたる方法を予測することは重要である。
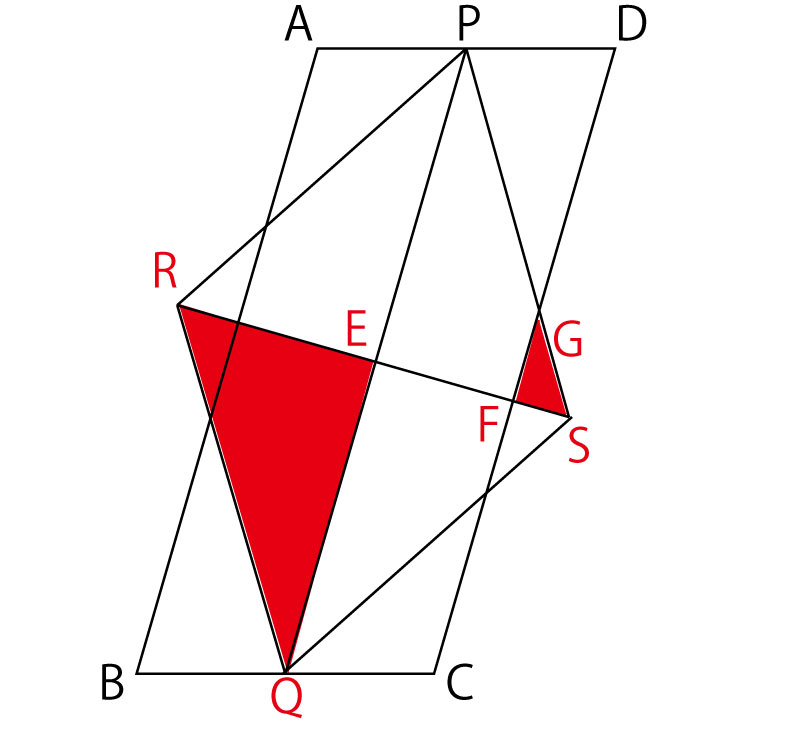
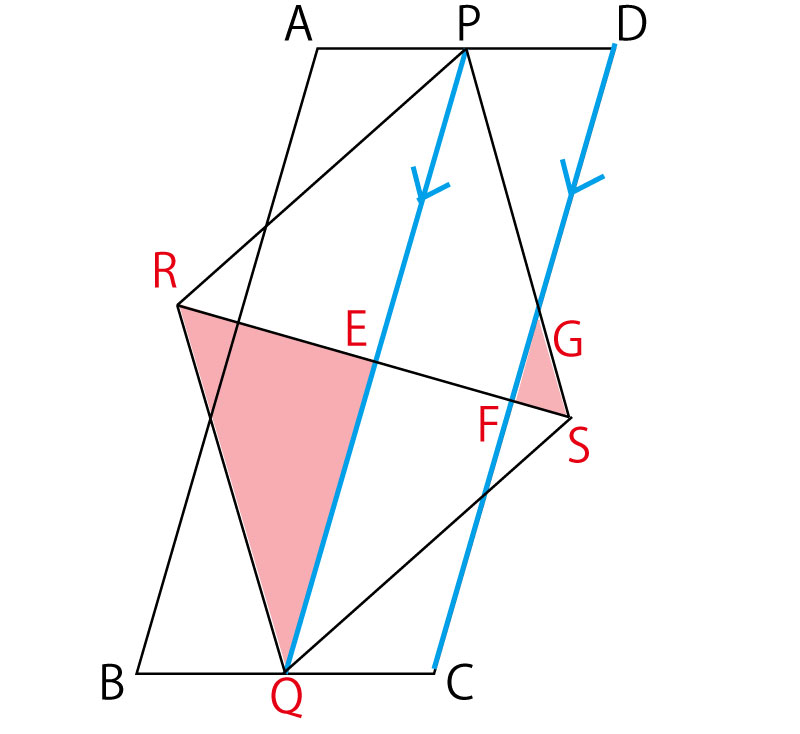
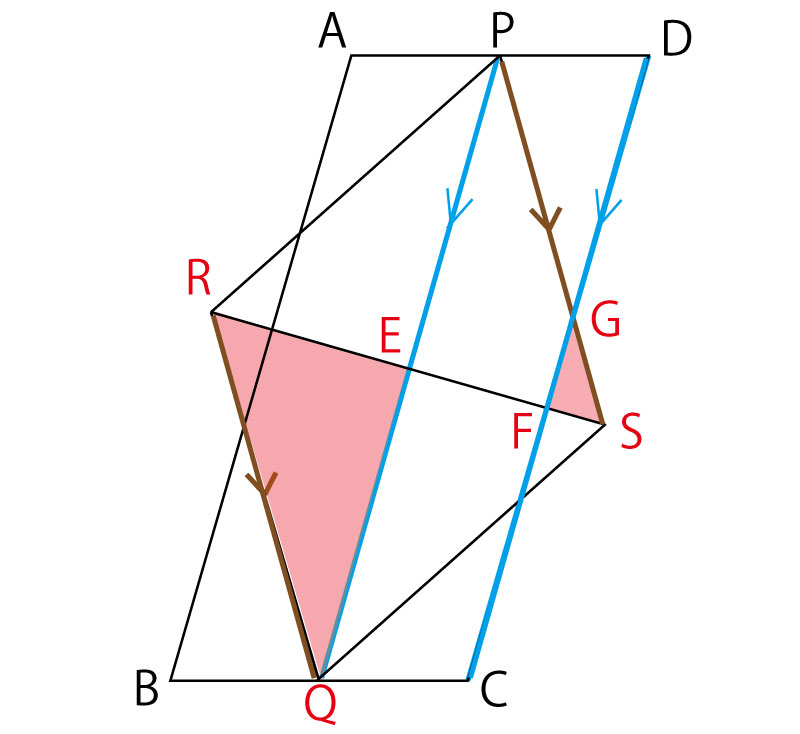
この証明の目的は△RQE∽△SGFという三角形の相似の証明である。まず、その三角形を図の中で確認してみよう。
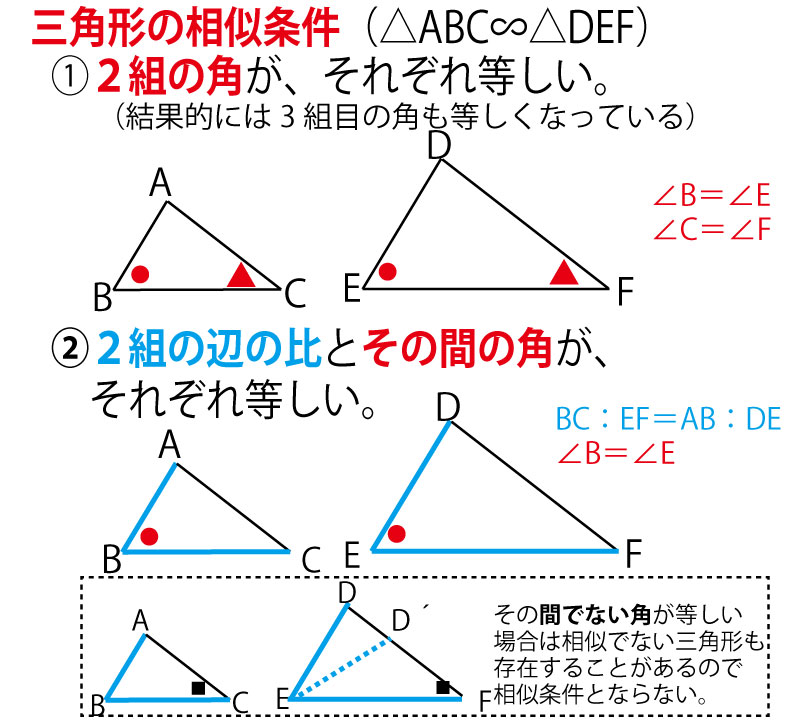
次の3つの「三角形の相似条件」のうちどれを使って証明していくのかを予測してみよう。
三角形の相似条件は教科書では、出る順番が逆で、
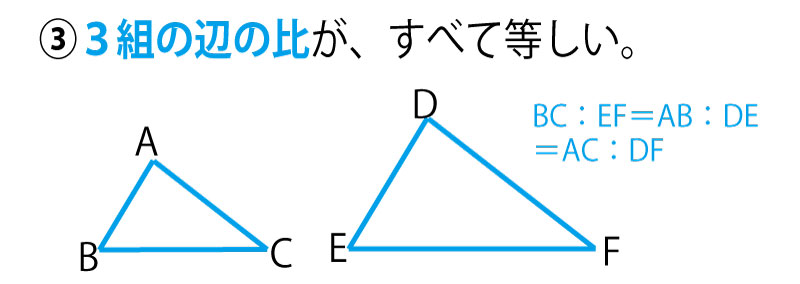
「3組の辺の比が、すべて等しい」
「2組の辺の比とその間の角が、それぞれ等しい」
「2組の角が、それぞれ等しい」
の順に書かれていることが多い。
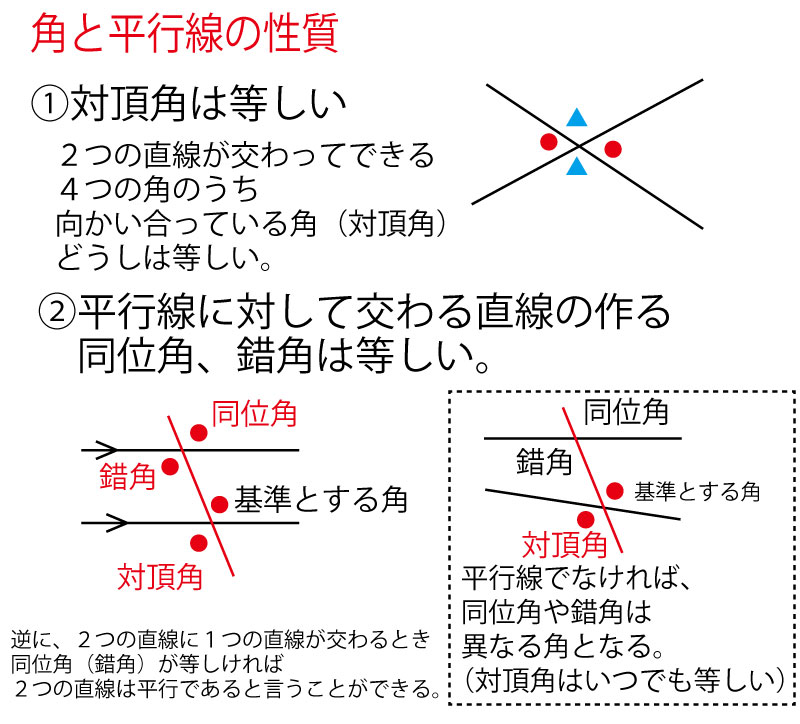
ただ、多くの「図形の証明」の入試問題は、辺比を数値で示すよりも、図形から、対頂角、平行線の錯角・同位角などを活用しながら「角が等しい」ことを見ぬかせて解かせる問題となっている。したがって、入試的には上記の番号順に使われると考えておいたほうがよい。
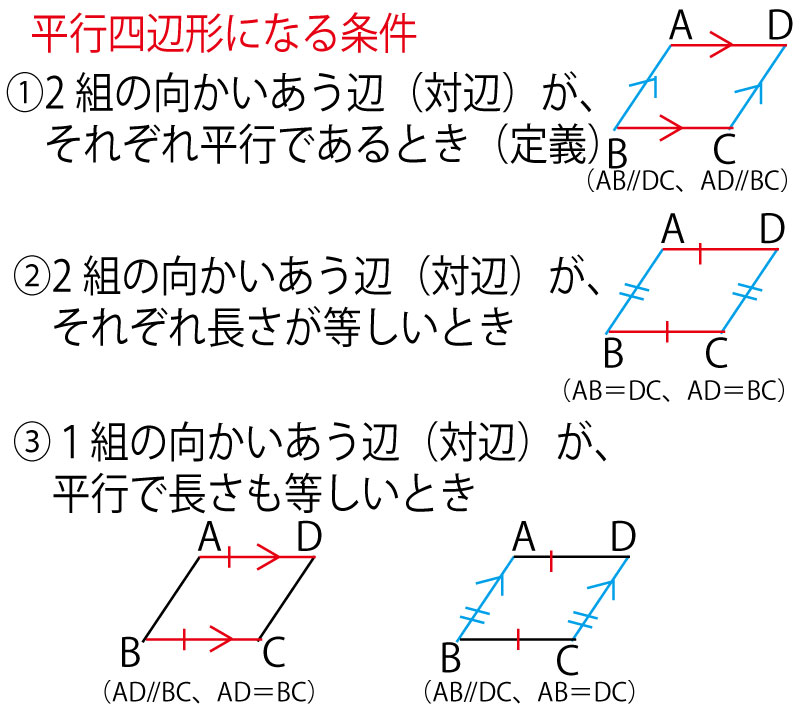
また本設問では平行四辺形ABCD、平行四辺形の一種であるひし形PQRSがあり、平行線の同位角・錯角で同じ角と証明できる素材が多いと予測できるのに対し、(「中点」という記述はあるものの)辺の比のヒントとなる長さの記述は少ない。したがって「2組の角が、それぞれ等しい」を使って、三角形の相似の証明をするだろうと予測できる。また証明の記述してある部分の前半の最後(手段)が平行線条件となっていることからも、その予測は裏付けられる。
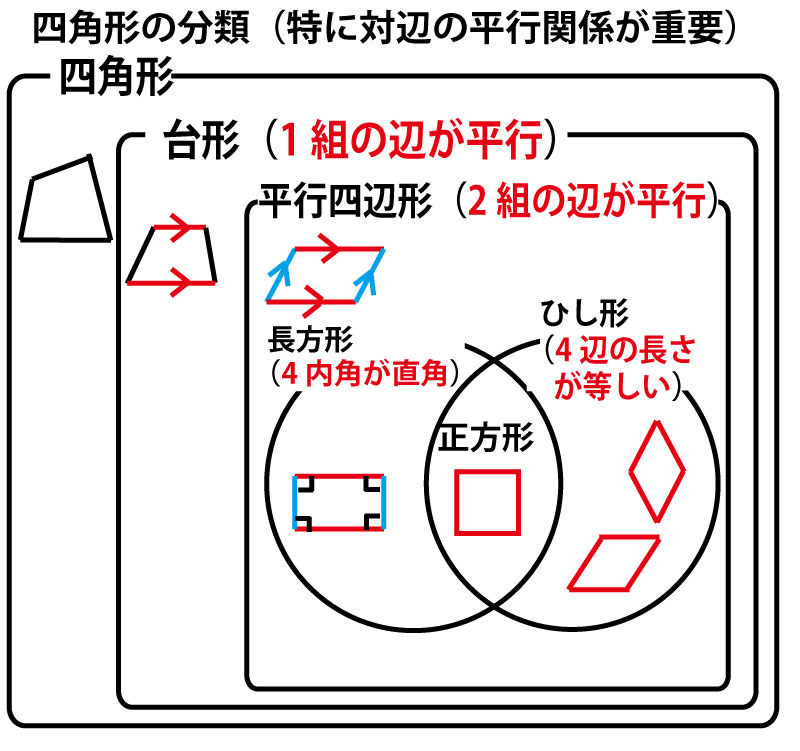
ひし形が平行線の一種である(つまりひし形の対辺は平行)であるということがわかっていれば、本文のひし形という記述を見ただけで、ひし形の対辺部分でも錯角・同位角が等しいことを証明に使うことができると予測できる。
このように名前の付けられた四角形(台形・平行四辺形・ひし形・長方形・正方形)を含む図形は、対辺が平行という平行条件の宝庫であり、錯角・同位角(そして対頂角)の条件で次々に角が等しいことを発見していく同じ角の発見の宝庫と考えよう。
さて、上記のような予測と、基礎知識を確認した上で解いていこう。
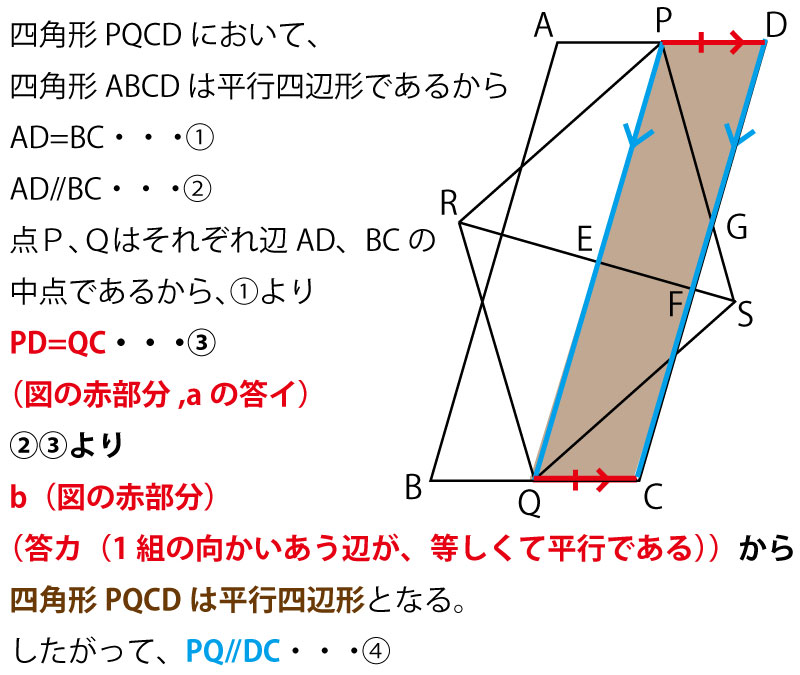
さて、ここまでで前半(手段)の証明まで到達した。ついに後半(目的)の証明の記述である。問題文には計3つの図がある。上の図を手段(証明前半)に使う図、真ん中の図を目的(証明後半)に使う図、最後の図は(2)の計算の思考に使う図と使い分けることを決めておくとよい。
目的をはっきりする上で、手段のために使った過程の図(上の図)はもう使わず、真ん中の図に手段の最後の結論(PQ∥DC)のみ書き込み、目的(△ABQ、△ABR)を意識した図を描こう。
ひし形(平行四辺形の一種)PRQSの平行な2組の対辺のうち、RQ∥PSが目的三角形の辺と重なっていることに気がつくと、平行線の錯角・同位角の関係が使えそうである。
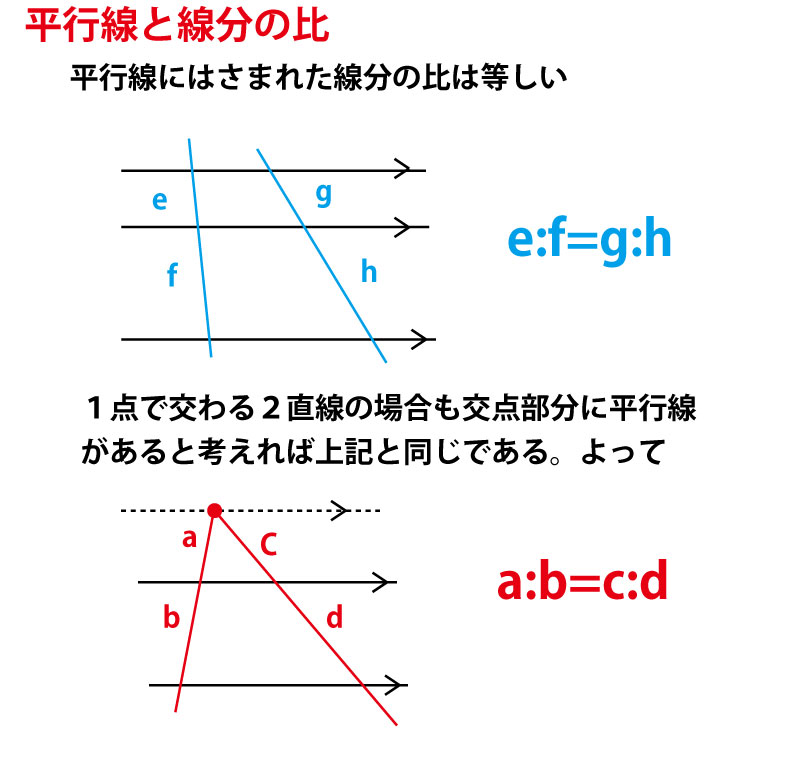
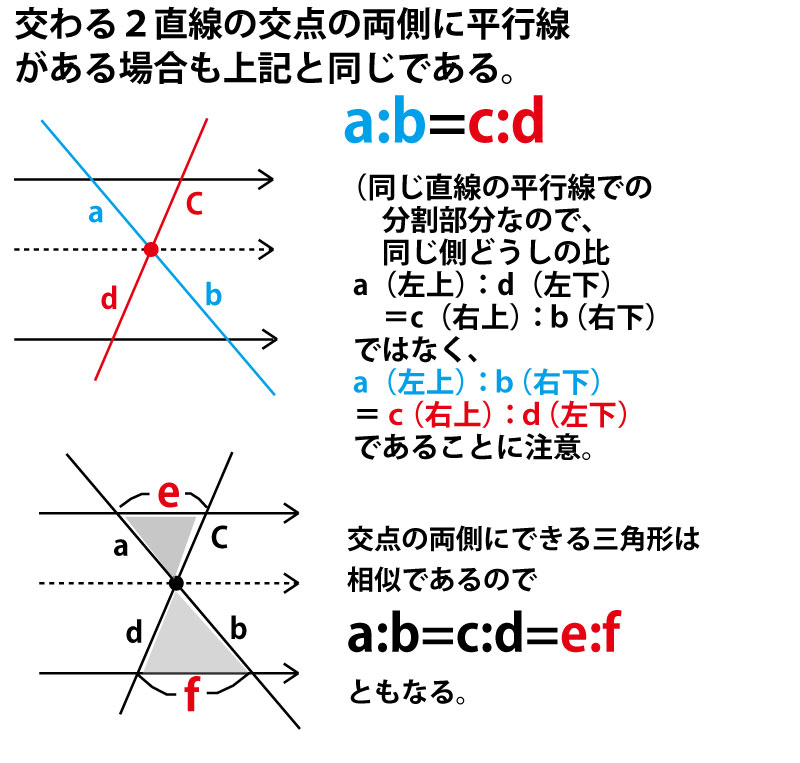
まず、平行線の錯角・同位角、そして対頂角のことを整理しておこう。
注目する2つの平行線を図に描きいれる。
すると、目的の2つの三角形の角のうち、2組の角が以下のように同じであることがわかる。
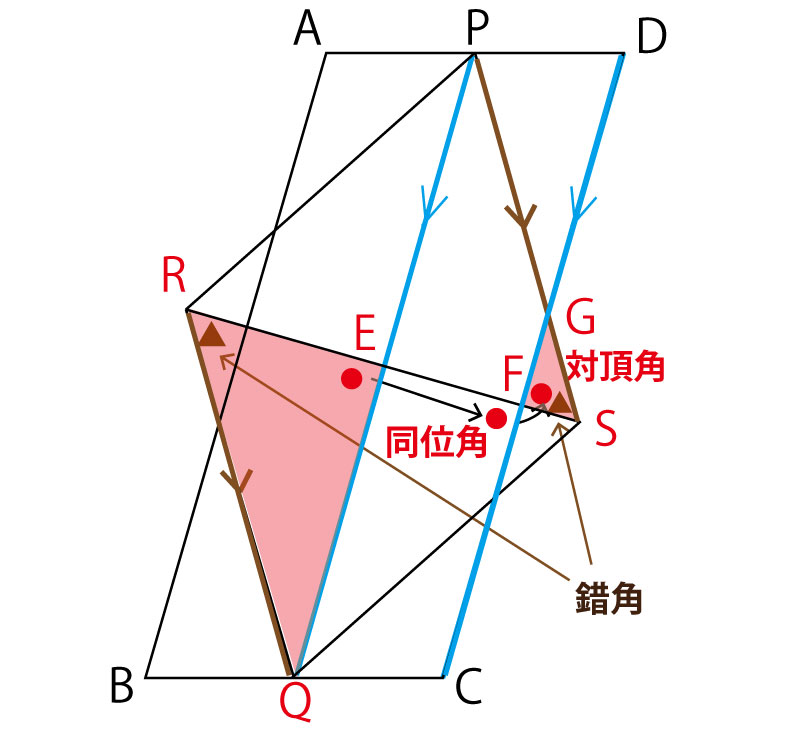
方針が決まれば、あとは文章化してcが完成する。
★実際の入試解答での注意事項
本解説では、理解をしやすいように図形を塗ったり、色の線を書き込んだりした。しかし、実際の試験場では、黒鉛筆(と消しゴム)しか使えず、色は使えない。そして鉛筆では図形を塗るのに時間がかかる。したがって以下のようにしたほうがよい。
1、図形の塗りつぶし→塗りつぶしには時間がかかるし角などが書き込みにくい。実際には塗りつぶさず、斜線を薄く引いて浮き立たせる。
2、線の強調→太く上からなぞる(とんがった鉛筆の他に、先が丸まって太く描ける鉛筆をもう1つ用意しておくとようかもしれない)。
3、角(本設問では、図を強調するため●と▲を多用した)→●や▲のように塗りつぶすのには時間がかかる。〇と×が簡略でお勧め。
4、図中の頂点のアルファベットの強調(本解説ではアルファベットを色に変えた)→強調したい頂点アルファベットを〇で囲む。
(2)解説
この計算問題は、千葉県教育委員会の発表によれば、正答率0.2%(500人に1人)であるので、できなくても差支えない問題ではある。しかし、この問題の解き方を確認することで、図形に伴う計算や定理を様々確認できる問題である。さすがに、千葉県教育委員会も、0.2%という正答率を反省し、2020年以降はもう少し解きやすい出題をしてくる可能性がある。その際、この問題を解く上で使う発想が役立って、きちんと正解にたどり着ける可能性もあるので、しっかり理解しておこう。
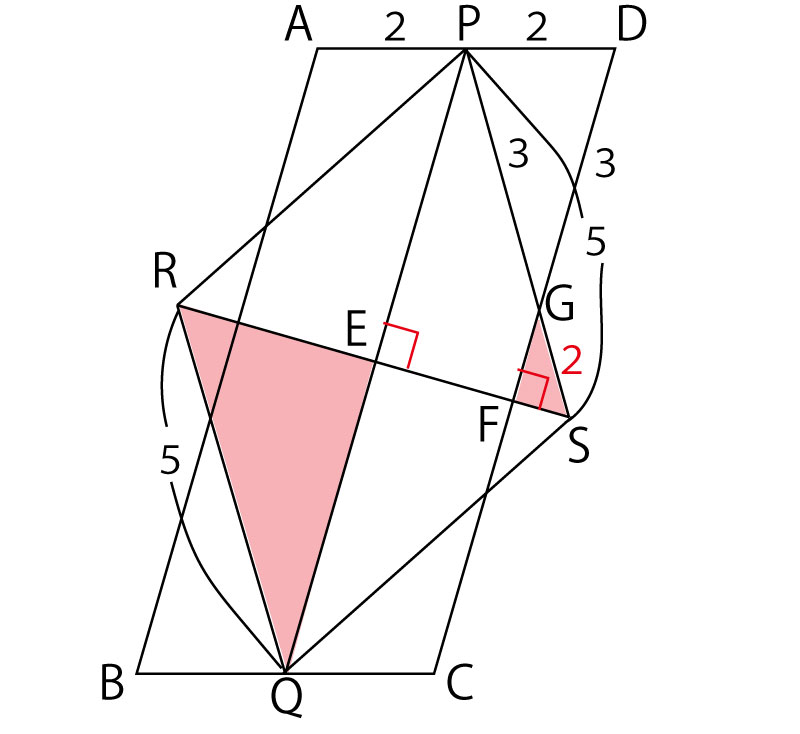
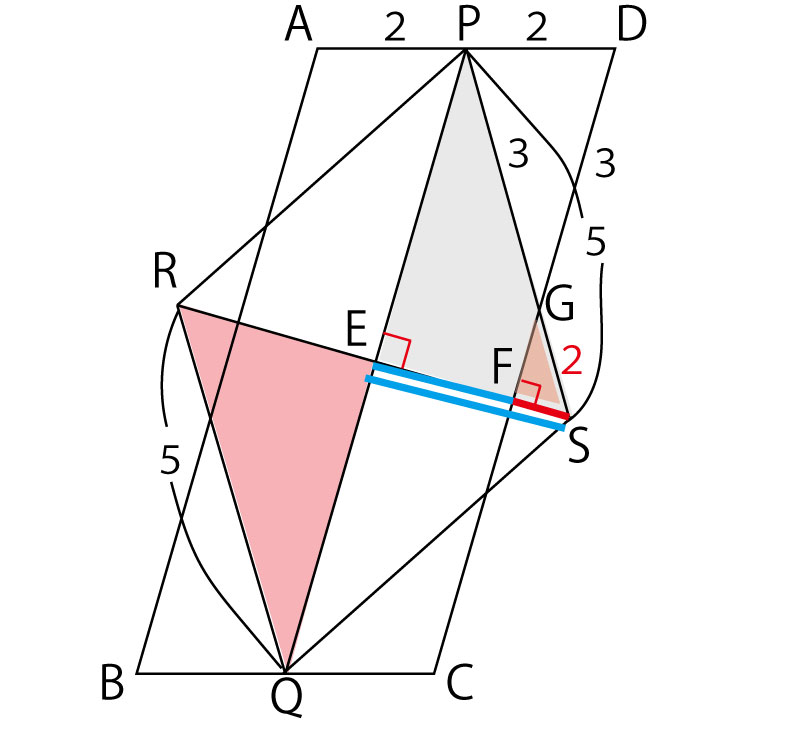
書き込みは一番下の図の中にしていく。答えにはcmという長さの単位があるが、まずはcmは省き、与えられた長さの条件を図の中に書き込んでみよう。
(1)cの証明の図では∠REQ=∠EFC=∠GFSを●で表現した。三角形の相似条件で「2組の角がそれぞれ等しい」ことを示せばよいだけだったので、実際に角度は考えなくてよかった。
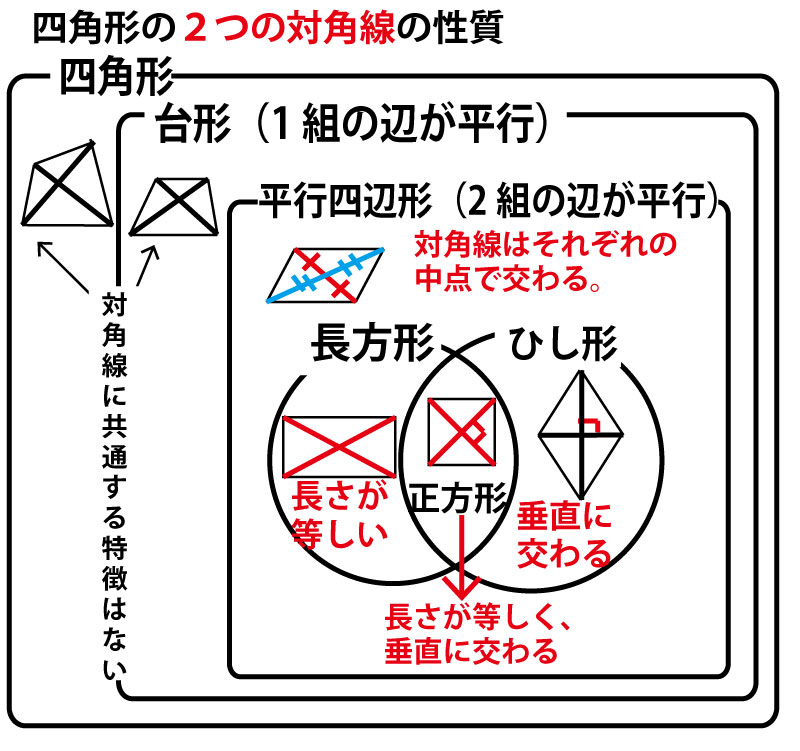
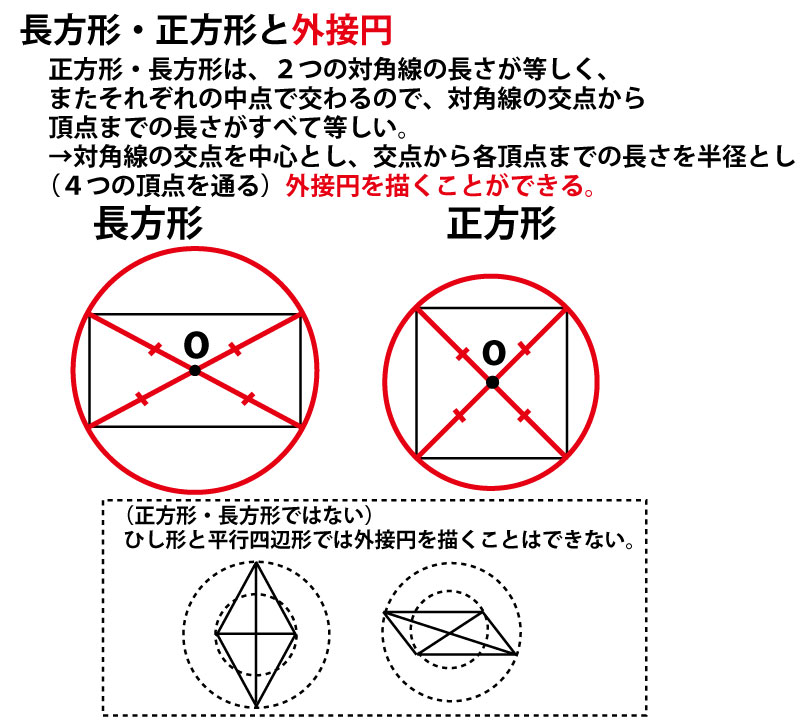
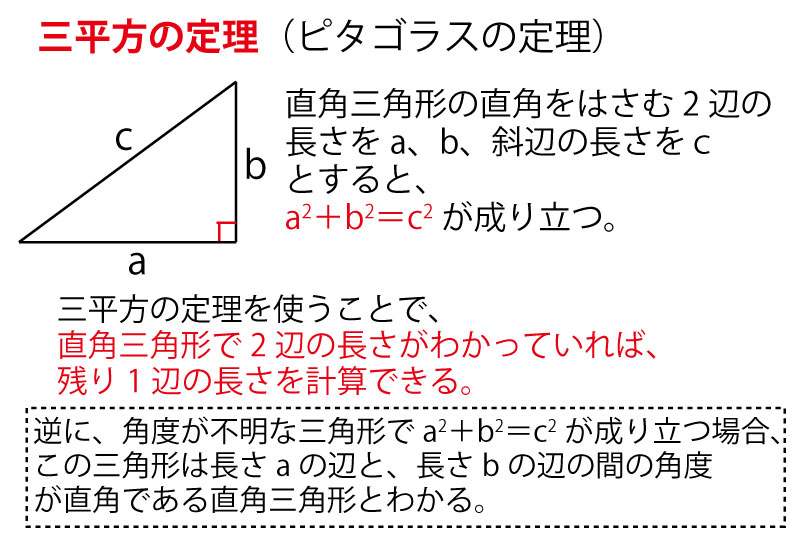
しかし四角形PRQSはひし形であり、Eはひし形の2つの対角線の交点であり、ひし形の対角線が直角に交わることを考えると、∠REQ=∠EFC=∠GFS=90°であるとわかる。長さを求めるときは直角三角形の三平方の定理を使うことが多いので、これからは直角であることを明記しよう。以下に四角形の2つの対角線の性質と(本設問では使わないが高校入試で問われることの多い)外接円の関係を整理したので確認してほしい。
四角形RQSPはひし形なのでRQ=SP=5であり、PG=3から、GS=2であることに気づくことが大切である。
また、千葉県では(2)(計算問題)は(1)cで証明した結果(△RQE∽△SGF)を使う。つまり、この場合、相似比を使うことが予測できるので、この2つの三角形も強調しておこう。
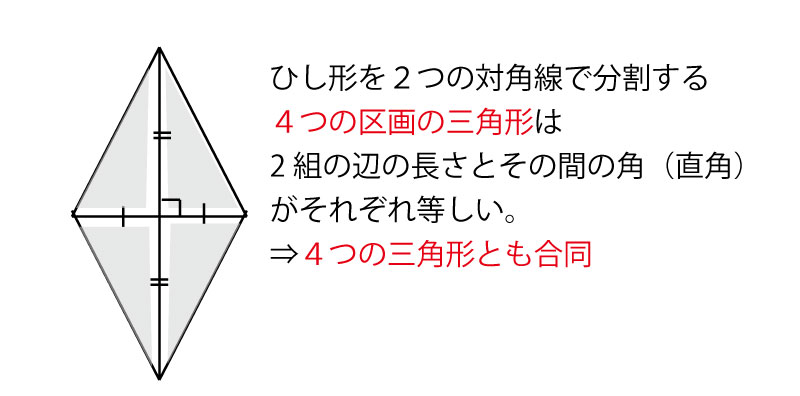
ひし形を2つの対角線で分離してできる4つの三角形は合同であるを活用して、この2つの三角形を更に比較しやすくしてみよう。
(1)cで掃除を証明した2つの三角形(△RQEと△SGF)はは離れているが、上記のようにひし形を2つの対角線で分離してできる4つの三角形は合同であることに気づくと、△RQE≡△SPEであり、△SPE∽△SGFに変換できることがわかると相似比を同じ側の図形で使うことができる。下図で△SPEを灰色で表現してみると、△SPEと△SGFは頂点Sを共有し、重なりあうので、相似であることが更にわかりやすく、相似比も使いやすそうになる。
この図で求めるべきFSとつながっているEFか(FSを一部含む)ESの長さを求めることができれば、相似比によりFSを求められそうである。そこでEF(かES)の長さを求めることを目標にする。
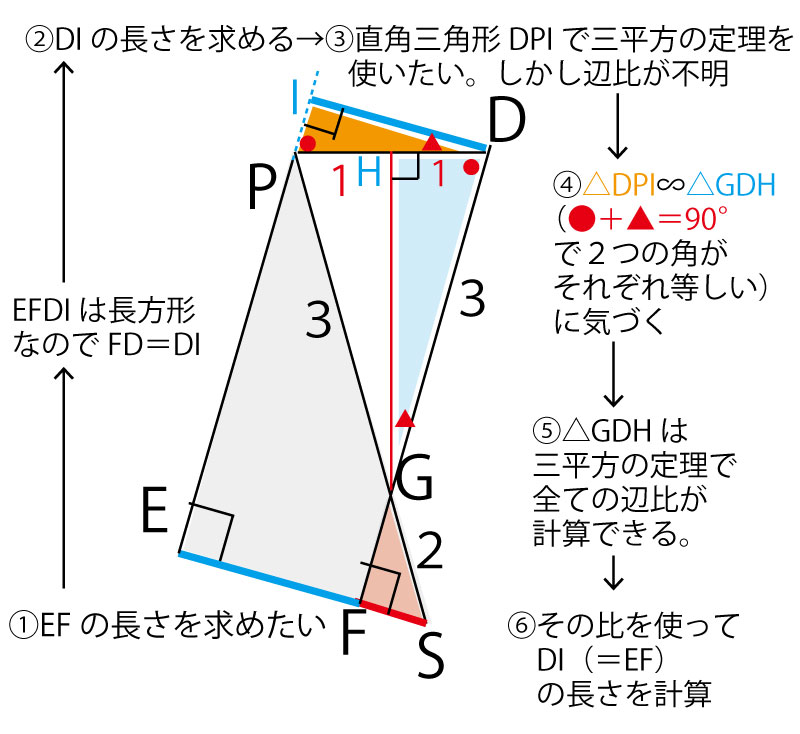
△RQEを△SPEに置き換えたことで、図の右上部分だけで考えられそうになってきたので、右上部分のみを強調して描いてみる。また点DからEPを延長した直線に垂線を下ろしその交点をIと置く。すると四角形DIEFは長方形になるので、EF=IDとわかる。IDを求めるにはオレンジの直角三角形△DPIに注目すれば三平方の定理が使えそうである。ただ、残念ながらPD=2だとはわかるが、DIもIPも長さがわからない。
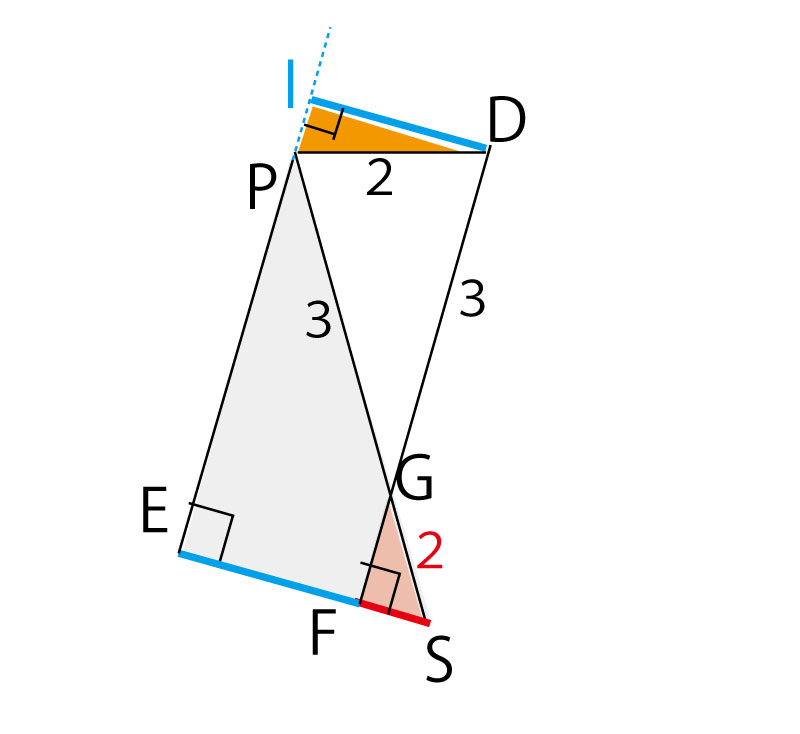
そこで、二等辺三角形△GDPにおいて「二等辺三角形の頂点から底辺におろした垂線は底辺の中点と交わる」性質を利用してみる。
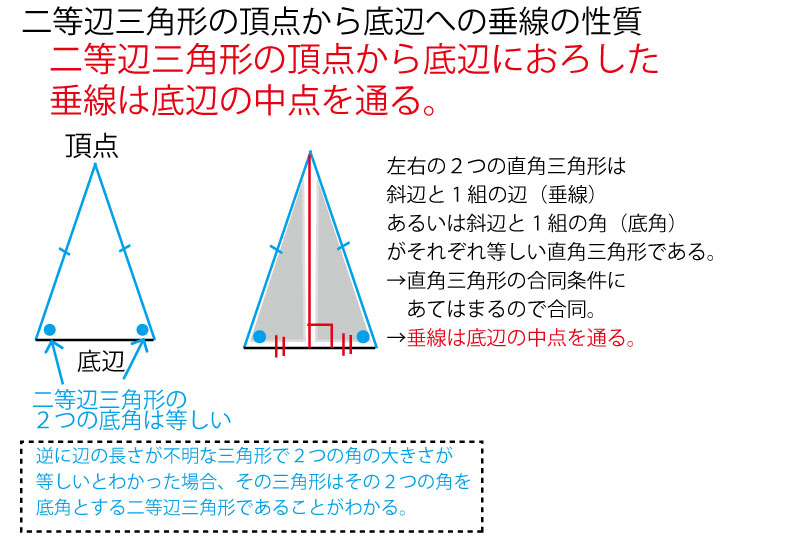
Gから定点PDに垂線を下ろし、PDとの交点をHとおく。すると垂線で分割されてできた直角三角形△GDHで3辺の長さと比がすべて三平方の定理で求められることに加えて。△DPI∽△GDHであることもわかり、DI=EFが求められそうである。
以上の発想の流れを以下の図にまとめたので確認してほしい。
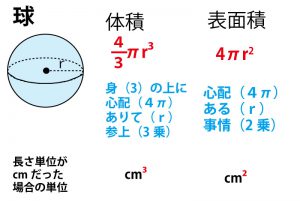
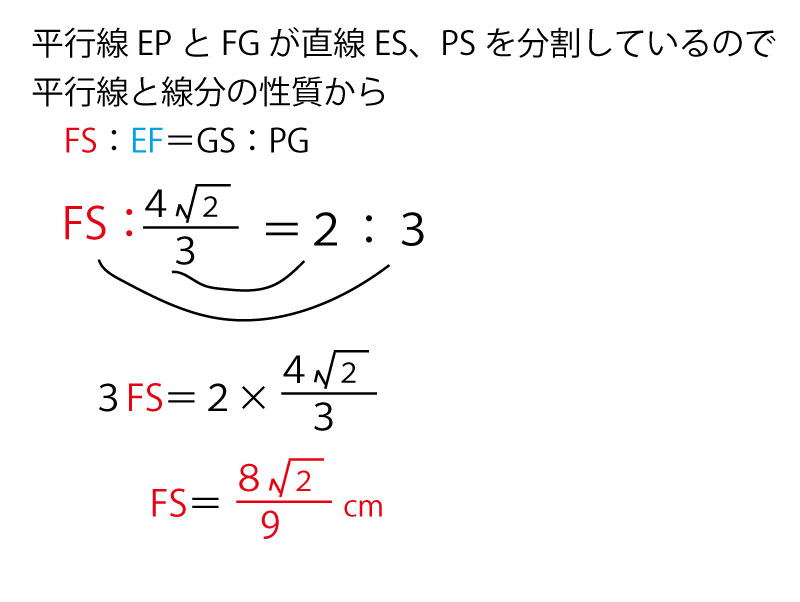
最後に、実際に計算してみるが、その前に、その計算に不可欠となる3つの事項を確認しておこう。
更に詳しく学びたい方は、アマゾンから拙著「図形の証明」「円」「三角形」をご購入いただけます。アマゾンのサイトより「朝倉幹晴」でご検索ください。