2019年前期、千葉県公立高校入試「数学」第5問（文章題）解答・解説

解説

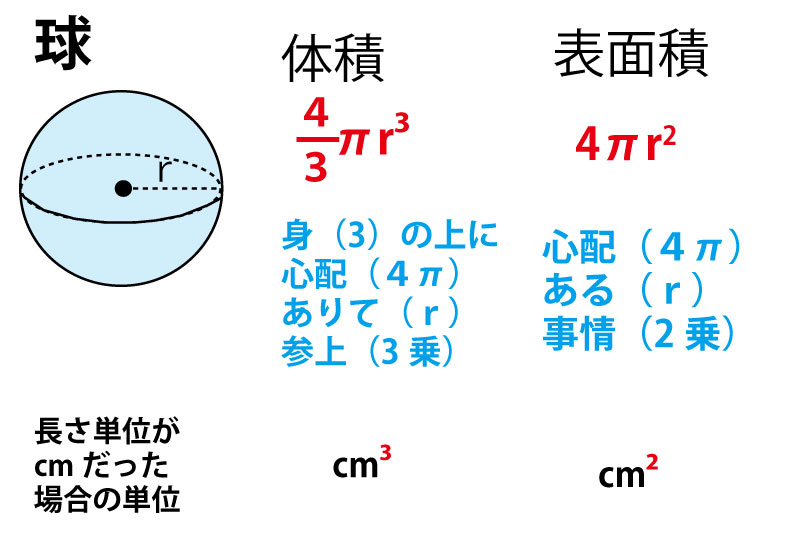
まず、体表的な立体の体積と表面積を整理しておこう。本設問では「体積」のみ聞かれているが、「表面積」（底面積・側面積）もよく問われるので、まとめて整理しておこう。

特に円柱と円錐は底面の半径が与えられ、円の面積の公式を使いながら求めさせる形での出題が多いのでとくに整理しておこう。
表面積の場合は側面積と底面積を分離して考えて合計する必要があるし、「側面積」「底面積」単独で聞かれることもあるのでそれぞれ把握しておこう。なお円柱の場合は、日常生活では下（床側）の円を底面（下面）、上側の面を「上面」と区別して表現することがあるが、数学の世界では両方とも「底面積」と表現し、底面が２つあるとみなす。

上記のように「円錐の側面積＝π×（底面の円）半径×母線」という簡略で便利な公式があるが、教科書ではこの公式は明記されず、この公式にいたる以下の考え方のプロセスを重視している。したがって高校入試においてもこのプロセスを問うてくる可能性があるので理解しておこう。母線とは、円錐の頂点から底面の円周のいずれかの位置に側面上に引いた線分であり、円錐の展開図のおおぎ形の半径となる。

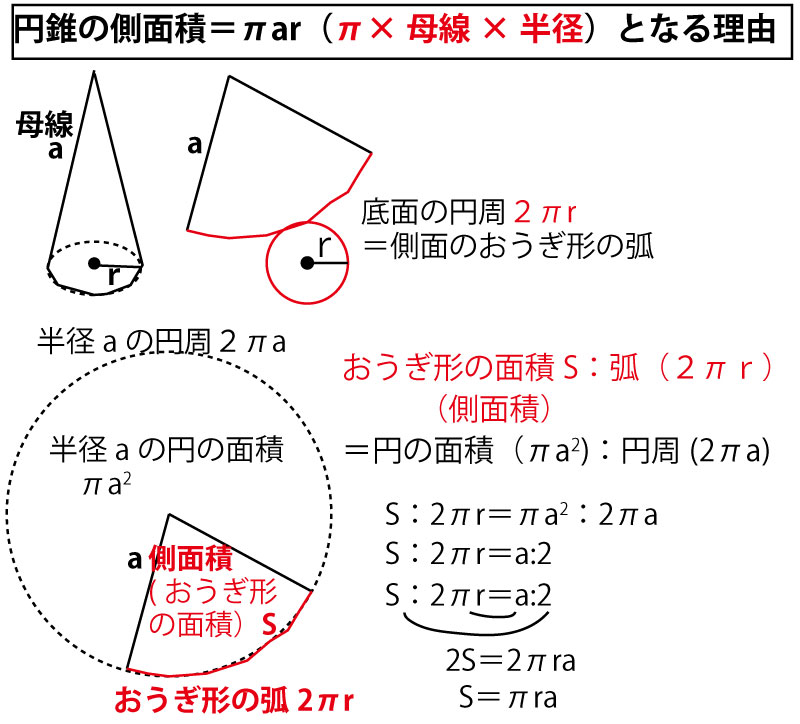
上記のように、おおぎ形と円の周囲（弧・円周）と面積を比例式で計算することで、「円錐の側面積＝π×（底面の円）半径×母線」

長さの単位がcmの場合、単位は以下のようになる。

千葉県公立高校入試では解答欄にあらかじめ印刷してくれているので間違えることはないが、他の高校入試を受ける人は単位の間違いは減点対象となるので気を付けてほしい。

それでは実際の問題の答を考えましょう。

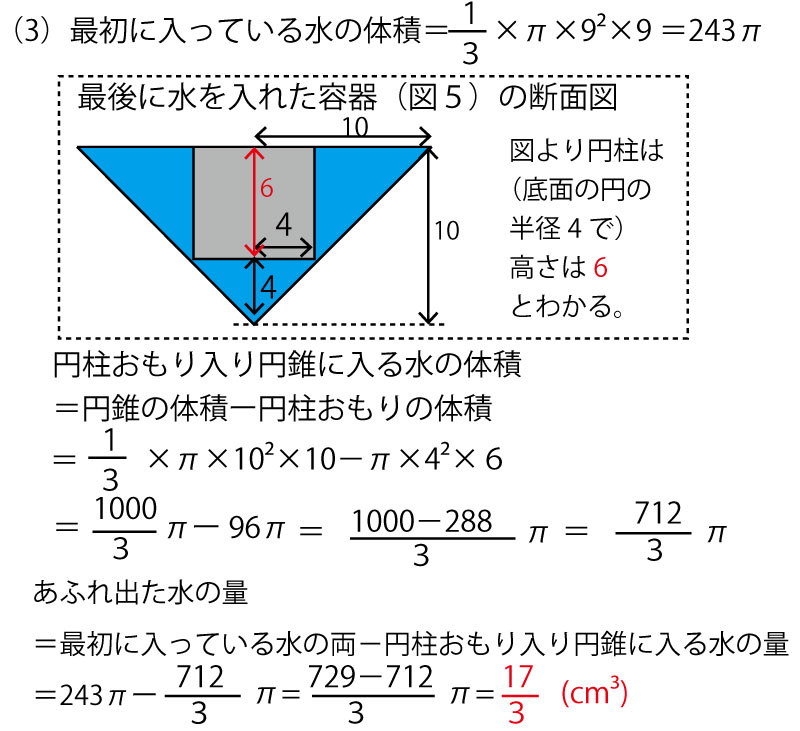
（2）の解説は上記の解答にある通りです。
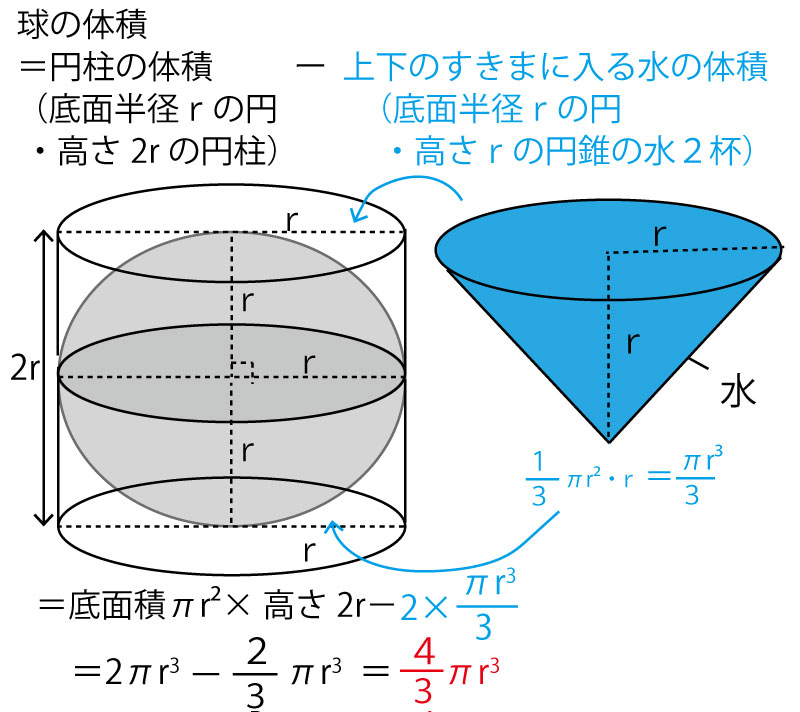
この設問では球の体積の公式を知っていて、水を入れるすき間の体積を求めさせる問題になっているが、中学の教科書では、この問題の流れと逆で、このすき間に入れあれる水の体積を使って、球の体積の公式を求める手段として使われている。

この問題にあるように容器Bのすきまと容器Aの円錐の体積は同じである。
そこで、以下の図のようにこの問題の容器Bを上下２つくっつけると、おもり部分が「球」になり、円柱の高さが2倍になる。そして高くなった円柱の体積から、上下のすきまにいれることのできる水（円錐の体積）を引くと球の体積の公式を求めることができる。