2021年、千葉県公立高校入試「数学」第3問（二次関数、配点計15点）問題・解答・解説

2021年7月12日　予備校講師・船橋市議　朝倉幹晴

2021年2月の千葉県公立高校入試「数学」の第3問（二次関数）の問題・解答、そして私（朝倉幹晴）が作成した解説です。千葉県教育委員会が発表した各問の正答率（無答率）も付記しました。なお、入試問題は白黒ですが、せっかくの画面上ですので、一部カラーにしました。ご活用ください。

第3問（配点計15点）

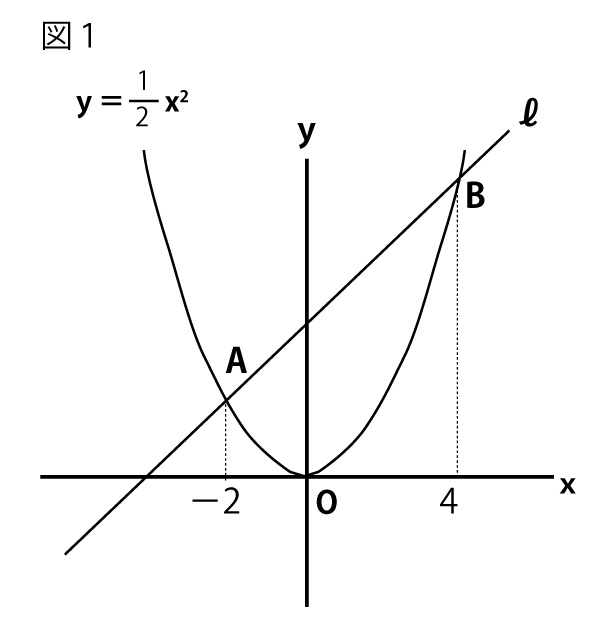
図１のように、関数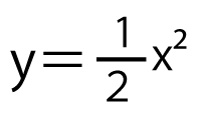のグラフと直線ℓが2点A、Bで交わっている。2点A、Bのｘ座標が、それぞれ－２、４であるとき、あとの（1）、（2）の問いに答えなさい。
ただし、原点Ｏから点（1,0）までの距離及び原点Ｏから点（0,1）までの距離をそれぞれ1cmとする。

（1）直線ℓの式を求めなさい。（配点5点）（正答率76.9％（無答率5.8%))

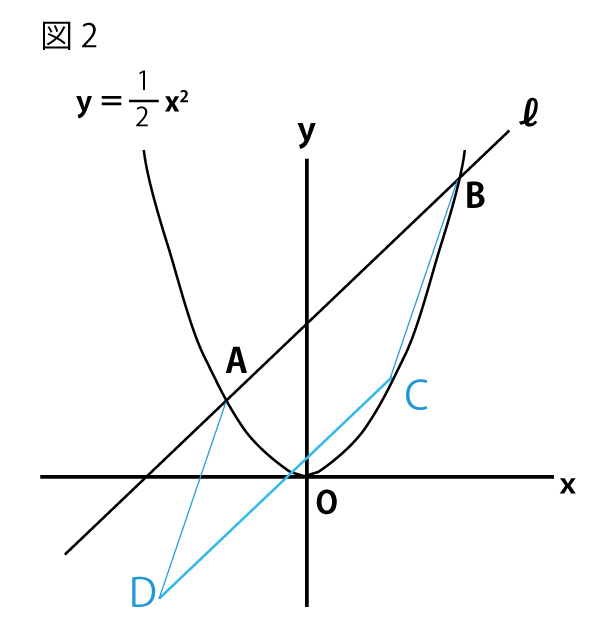
（2）下の図２のように、図１において、関数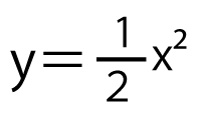のグラフ上にｘ座標が－２より大きく４より小さい点Ｃをとり、線分ＡＢ、ＢＣをとなり合う2辺とする平行四辺形ＡＢＣＤをつくる。このとき、あとの の問いに答えなさい。

点Cが原点にあるとき、平行四辺形ABCDの面積を求めなさい。（5点配点）（正答率29.5%(無答率29.6%))

平行四辺形ABCDの面積が15cm²となるとき、点Dのｙ座標をすべて求めなさい。（5点配点）（正答率2.5%(無答率65.6%))

[next_p]