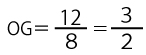2021年、千葉県公立高校入試「数学」第3問(二次関数、配点計15点)問題・解答・解説
【解答】(計15点配点)
(1)y=x+4(配点5点)(正答率76.9%(無答率5.8%))
(2) 24(cm2)(5点配点)(正答率29.5%(無答率29.6%))
24(cm2)(5点配点)(正答率29.5%(無答率29.6%))

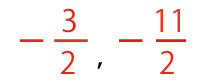 (5点配点)(正答率2.5%(無答率65.6%))
(5点配点)(正答率2.5%(無答率65.6%))
【解説】
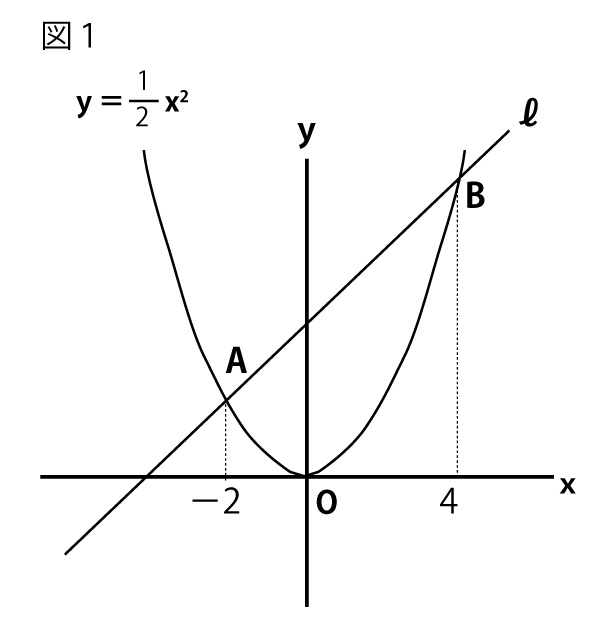
(1)A、Bは![]() 上にあるので、y座標をもとめると
上にあるので、y座標をもとめると
A:y=1/2 ×(-2)2=2
B:y=1/2 ×42=8
よって座標はA(-2,2)、B(4、8)である。
直線ℓをy=ax+bとする。直線ℓは2点A、Bを通るので、
2=-2a+b・・・![]()
8=4a+b・・・![]()
![]() -
-![]() より 6a=6 a=1
より 6a=6 a=1
![]() に代入して、2=-2×1+b b=4
に代入して、2=-2×1+b b=4
よってy=x+4
(2)
平行四辺形の面積の公式は以下の図の通りである。また平行四辺形の面積を求める別の方法として、対角線で分割すると2つの合同な三角形に分割されるのでその三角形の面積を求めて2倍するという方法もあることを知っておくとよい。
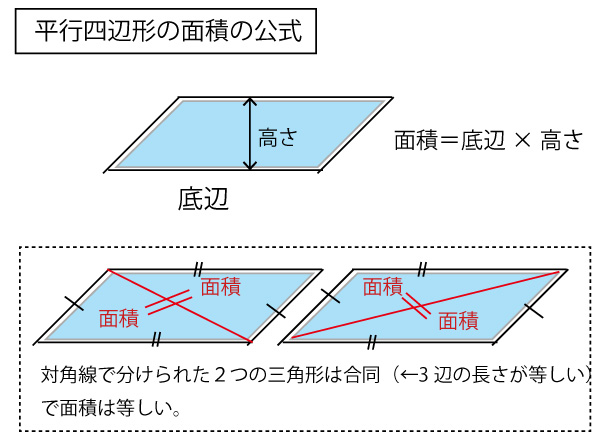
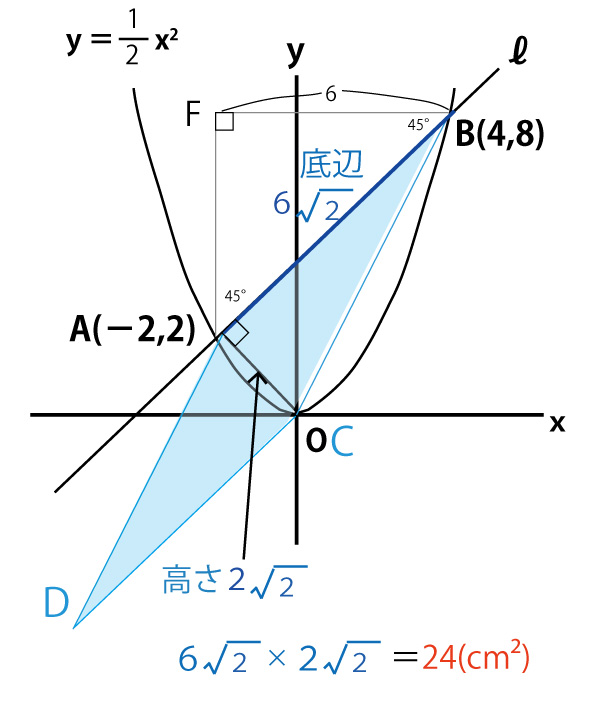
まず、本設問を、「面積=底辺×高さ」で求めてみよう。
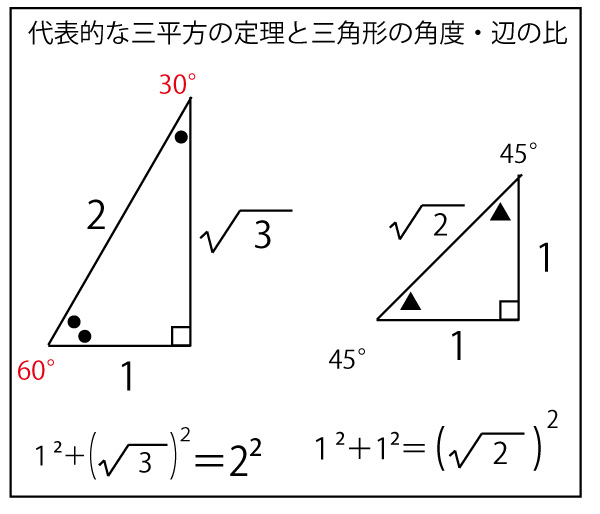
直線ℓの傾きが1であ、x軸、y軸に対して45°の角となる。するとAとBの位置からy軸、x軸に平行な線を引き交点をFとすると△FABは直角二等辺三角形となる。すると直角二等辺三角形の辺比(下図参照)からAB=![]() となる、同様にAC=
となる、同様にAC=![]() でAB⊥ACなので底辺AB(
でAB⊥ACなので底辺AB(![]() )、高さAC(
)、高さAC(![]() )の平行四辺形と考えることができ、面積24cm2を求めることができる。
)の平行四辺形と考えることができ、面積24cm2を求めることができる。
★2分割した三角形の面積で求める方法
上記のように平行四辺形を「底辺×高さ」で求めようとした場合、たまたま、本設問の場合は、辺ABの直線の傾きが1で、x軸、y軸から45°の角度であり、直角二等辺三角形の辺比からABの長さを容易に求められたし、AB⊥ACから、高さも求めやすかった。しかし、辺の直線の傾きは1や-1とは限らず、直交する「高さ」も求められるとは限らない。
したがって、別の発想を使ってみよう。
そこで、平行四辺形が対角線で2つの合同な三角形に分割されることを利用し、その三角形の面積を2倍して平行四辺形の面積を求めることを考えてみよう。
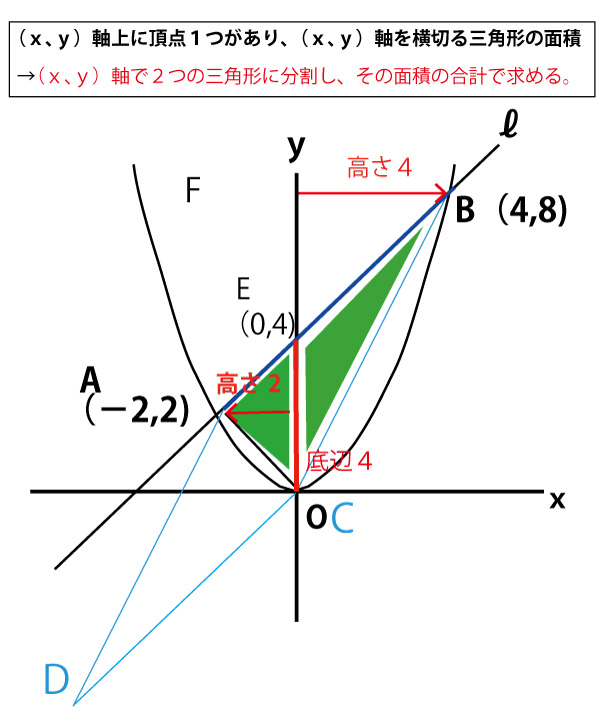
この図の青塗りの△AOB(△ACB)を考えてみる。先ほどと同じく、「ABの傾き1、AC⊥AB」という考えを使わなくても(その考えに気づかない場合でも)、発想を変えるだけで容易に求められる。高校入試では、(上記で説明した方法よりも)この解き方のほうが標準的であり、千葉県公立高校入試「数学」では好まれて出題される)
この三角形は、y軸上に頂点1つ(O、C)があり、y軸を横切る三角形である。その場合、y軸でこの三角形を2分割することで共通の底辺(この場合OE=長さ4)を持ち、残りの頂点A、Bのy軸との距離(x座標の差異)を高さにする図で緑で塗った2つの三角形に分割できる。底辺がy軸上の線分の長さになるので、高さはそれと直交するx軸との平行線の長さ、すなわちx座標の差異となる。すると3頂点ならびに、軸と三角形の辺の交点(E)の座標の数字を使うだけで容易に計算ができる。
この発想は、x軸上に頂点の1つを持ち、x軸を横切る三角形の面積を求める場合も同様に使うことができる。

(上記計算では「の面積」と書いたが、単に△ABO=△AEO+△BEOと書いてもよい。=は面積が等しいことを示す。(≡の場合は面積だけでなく形も完全に等しいことを示す))
![]()
一般に、数学の問題では、前の小問の答が、次の小問のヒントになっていることが多い。![]() の平行四辺形ABCD(ABOD)の面積24cm2の活用を考える。
の平行四辺形ABCD(ABOD)の面積24cm2の活用を考える。
平行四辺形ABCDは、C(とD)の位置によって形は変化しても辺ABだけは共通である。したがって、底辺をABと考え、面積を考えるとよい。
面積の比は
![]() の平行四辺形ABCD(ABOD):
の平行四辺形ABCD(ABOD):![]() の平行四辺形ABCD =24:15=8:5
の平行四辺形ABCD =24:15=8:5
底辺ABは共通なので、![]() の高さ:
の高さ:![]() の高さ=8:5となる。
の高さ=8:5となる。
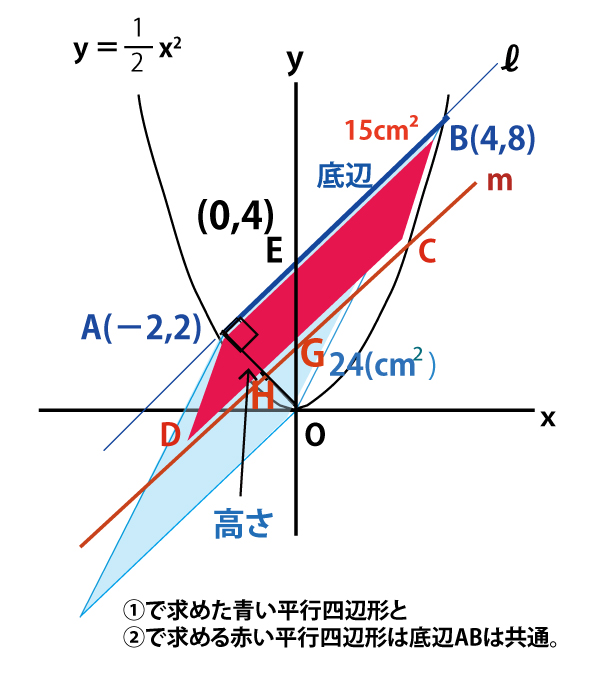
AB⊥AOであり、
![]() の平行四辺形ABCD(ABOD)は底辺AB、高さAO。
の平行四辺形ABCD(ABOD)は底辺AB、高さAO。
したがって、AO上の点HがAH:AO=5:8となれば、そのAHの長さが![]() の平行四辺形ABCD の高さとなる。
の平行四辺形ABCD の高さとなる。
Hを通り、ℓ(y=x+4)に平行な直線、図の直線m上に、底辺ABの対辺CDがある形になれば、高さはAHと同じになるので、面積は15cm2となる。
直線mとy軸の交点をGとする。
△OHG△OAEなので、
OG:OE=OH:OA=(OAーAH):OA=8ー5:8=3:8
よって直線mは直線ℓと平行なので同じ傾き1でOG(つまりy切片)が![]() なので、
なので、
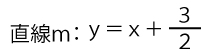
★2次関数の過去の出題
2020年前期、第3問(二次関数)(計15点)
2019年前期、第3問(二次関数)(計15点)
2018年前期、第3問(二次関数)(計15点)
2017年前期、第3問(二次関数)(計15点)
2016年前期、第3問(二次関数)(計15点)
2015年前期、第3問(二次関数)(計15点)
2014年前期、第3問(二次関数)(計15点)