2013年前期、千葉県公立高校入試「数学」第２問（2）（図形と角度）（配点5点）問題・解答・解説

【解答】118°（5点配点）（正答率43.9%(無答率13.8%))

【解説】

解いていく流れ

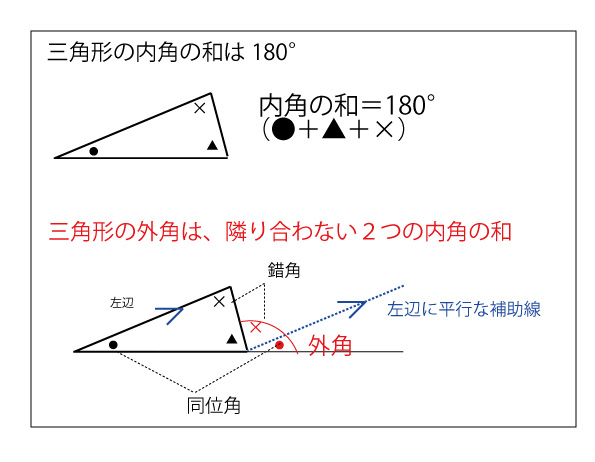
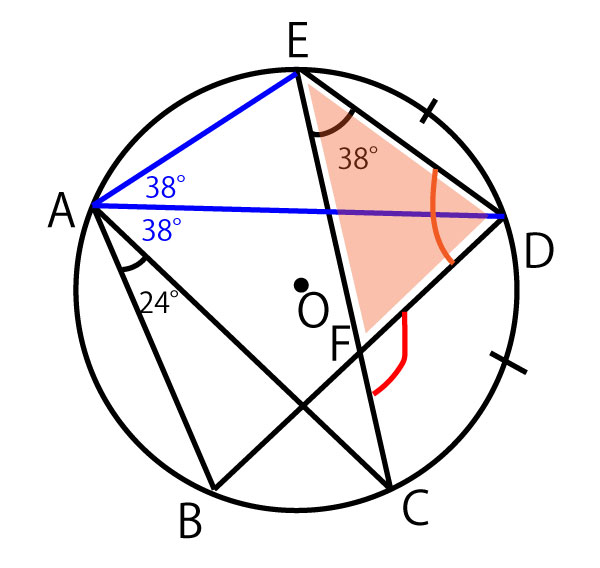
まず、図で求めるべき∠CFDは、オレンジの△EDFで「三角形の外角はとなり合わない２つの内角の和」を活用すれば、∠EDFさえ求めることができれば求めることができると発想する。そして∠EDFを求めることに、円周角の定理などが使えるではないかと発想をし、以下の流れを考えていく。

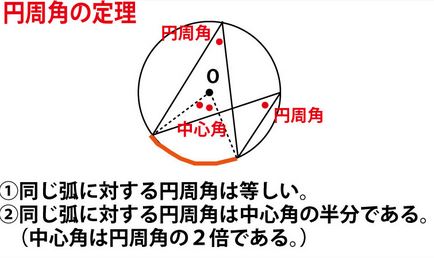
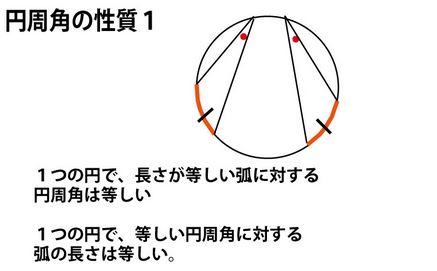
１，まず、図の青のように、に注目し、補助線を引きながら、円周角の定理を活用して、角度を求めていく。
２、円に内接する四角形AEDBに注目する。円に内接する四角形で対角（対面する内角）の和は180°であることを活用し、∠EDFを求める。
　　∠EDF＋∠EAB＝180°
∠EDF＝180°ー∠EAB＝180°ー（38°＋38°＋24°）＝180°ー100°＝80°

３、最後に、オレンジの△EDFに注目し、「三角形の外角はとなり合わない２つの内角の和」を活用すると、目的の∠CFDを求めることができる。

∠CFD＝∠FED＋∠EDF＝38°＋80°＝118°

★円周角の定理と円周角の性質１～４（今回は１と４を使った）