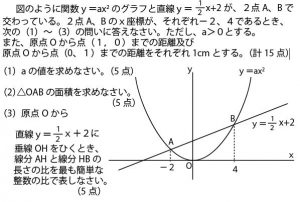
【2017年前期・千葉県公立高校入試数学】第2問(5)（作図）問題・解答・解説

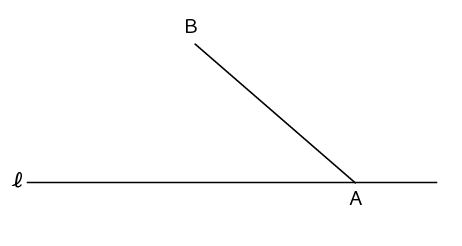
【解答】

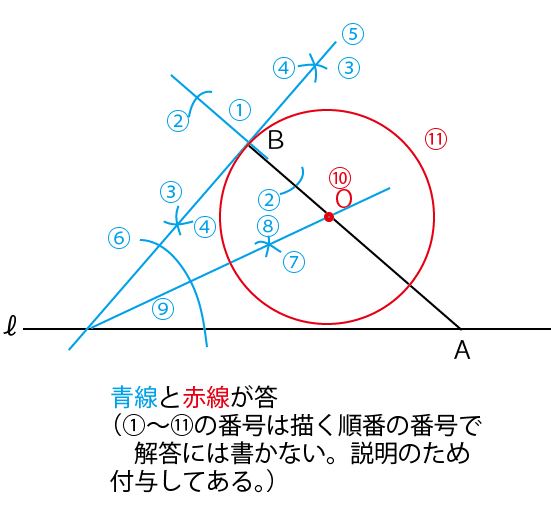
作図順番①～⑪の解説
①ABをB側に延長
②Bを中心の円を描く
③④、②の2点からの円を描く
⑤、③④の2交点を結ぶ直線
（⑤はBを通るABの垂線）
⑥ℓと⑤の交点から円を描く
⑦⑧、⑥の2点から円を描く
⑨、ℓ⑤の交点と⑦⑧の交点を結ぶ直線
（⑨は⑤とℓではさまれた角の二等分線）
⑩、⑨とABとの交点が円の中心
⑪、Oを中心としOBを半径とした円を描く

【解説１】（問題を解く上での前提知識）
★どの年の問題での出題されていることが多い３種類の作図
千葉県公立高校入試、第2問（5）の作図の問題では、作図に関わる様々な手法や知識が問われるが、一番使われる作図法は「垂直二等分線」と「角の二等分線」の作図である。どの年の問題でもこの２つのうちどちらかがを使う作図が出題されていると考えてほぼ間違いない。作図法を確認しておこう。

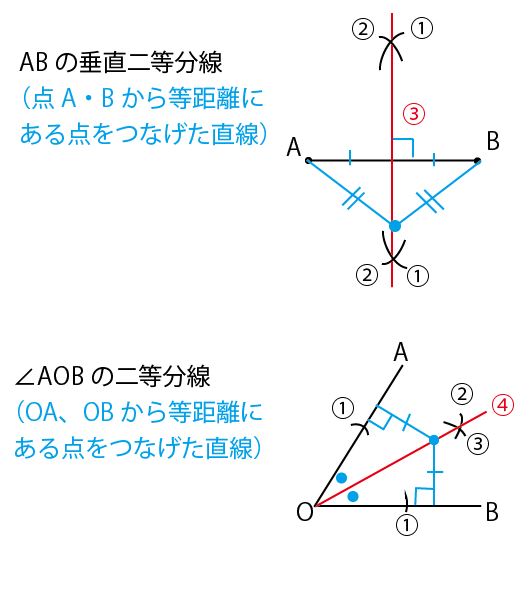
★次によくつかわれるのは垂線に関する作図である。作図法を確認しておこう。

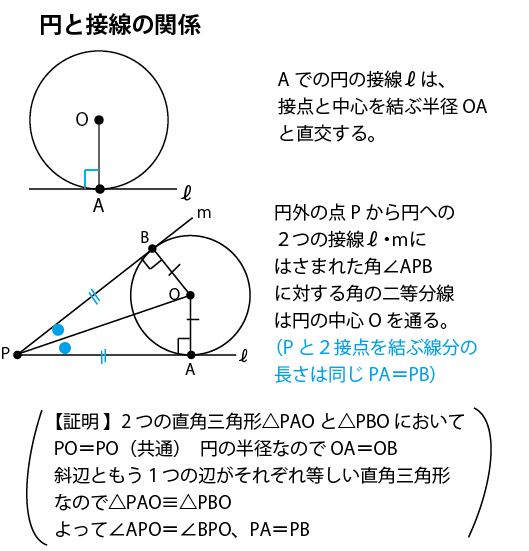
★円と接線との関係
作図の方針を考えていくためには、小中学校で学んだ三角形・四角形・円・角度などに関する様々な性質を知っておく必要がある。本設問で必要となる円と接線の関係を確認しておこう。

【解説２】（本問題を解く方針を立てる）
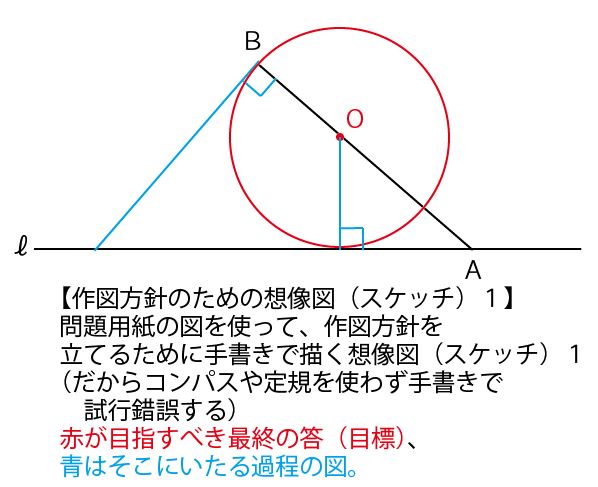
問題を解いて解答用紙に作図を描いていくためには、まず問題文の図の中に様々な鉛筆でスケッチを書き込みながら方針を立てる必要がある。上記【解説１】が理解できていれば、次の順番で方針を立てることができる。

①中心OがAB上にあり、円周上にBがあるということは、OBが円の半径になるということである。すると、Bを通るAB（OB）に対する垂線を描けば、それがBでの円の接線となる。

②、①でBでの接線とℓとの交点がわかると、円への２接線（ℓとBでの接線）ではさまれた角の二等分線上とABの交点に円の中心があるとわかる。

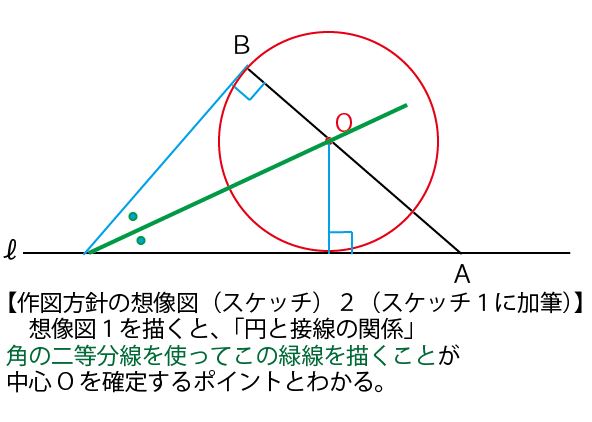
このスケッチを元に、解答用紙に【解答】のように作図して完成