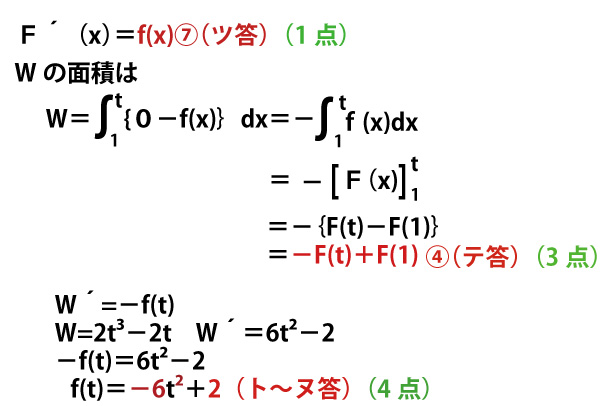2018年大学入試センター試験「数学ⅡB」第2問（計30点）問題・解答・解説

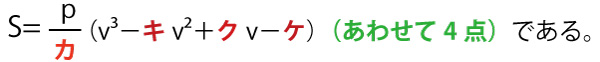
［解説］
［１］（1）

ｐ＞０とする。座標平面上の放物線ｙ＝px²＋qx＋ｒをＣとし、直線ｙ＝2x－１をℓとする。Ｃは点Ａ（1,1)においてℓと接しているとする。
（1）ｑとｒを、ｐを用いて表そう。放物線Ｃ上の点Ａにおける接線の傾きは２（ア答）（1点）である。
ｙ´＝2px＋q   よってx=1での接線の傾きは　ｙ´＝2p・１＋q＝2p+q。これが２となるので2p+q=2 。  q=－2ｐ＋2（イウエ答）（あわせて2点）。
さらに、Ｃは点Ａを通ることから、１＝p・1²＋q・１＋r  。  1=p+q+r 。  ｒ＝1－p－q=１－p－（－2p+2)＝１＋p－2＝p－１（オ答）（2点）となる。

（2）



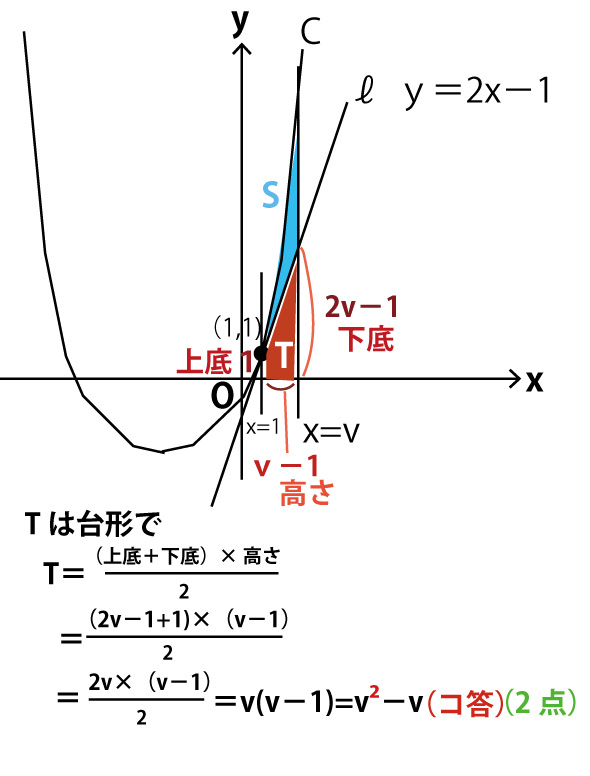
U´＝pv²−2(p+1)v＋(p+1)にｐ＝３を代入して
Ｕ´＝3v²−8v＋4＝(3v－2)(v－2)

最小値は極小値となるのでｖ＝２の時のＵの値である。
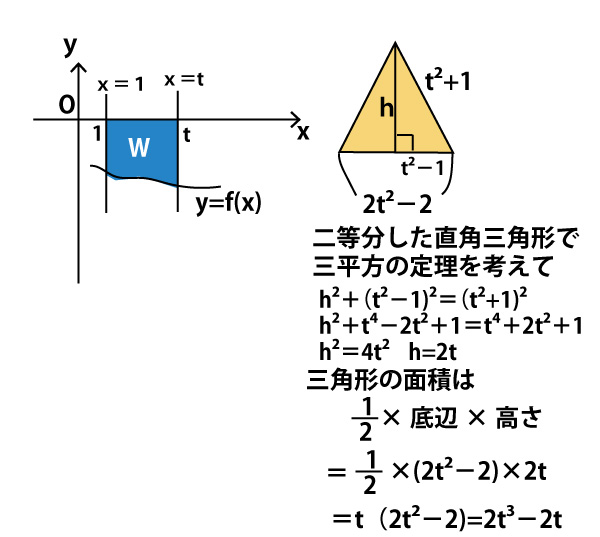
Ｕ＝V³－4V²＋4V－１＝2³－4・2²＋4・2−１＝８－16＋８－1＝－１（タチ答）（3点）

[2]