2019年前期、千葉県公立高校入試「数学」第2問（3）（方程式・文章題）問題・解答・解説

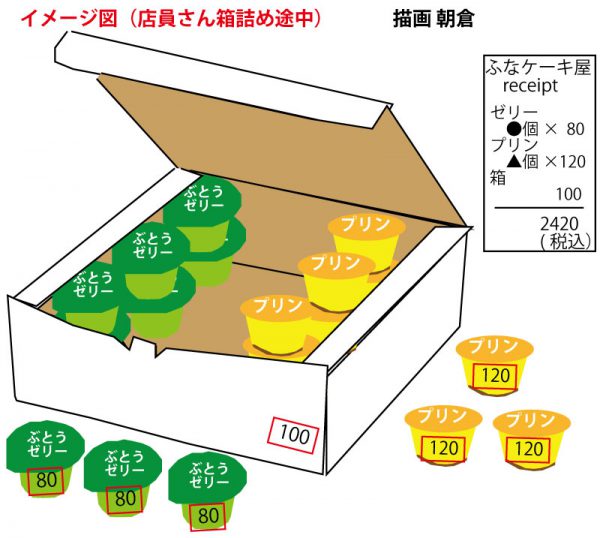
第2問（3）解答　14個

（5点配点）（正答率61.2%（無答率8.7%))

★解法１（一次方程式だけで解く解き方）
セリーをx個とすると、プリンは（24－x）個である。
合計金額より　100＋80ｘ＋120（24－x)＝2420
80ｘ＋120（24－x)＝2320
両辺を10で割ると　8x+12(24－x)=232
さらに両辺を４で割ると　2x＋3(24－x)=58
2x+72－3x＝58
－x=58－72＝－14
ｘ＝14　ゼリーは14個
（プリンは10個）

★解法２（連立方程式での解き方）
ゼリーx個、プリンｙ個とする。
個数合計より　ｘ＋ｙ＝24・・・（1）
合計金額より　100＋80x＋120y＝2420・・・（2）

この連立方程式を解く。

（2）を変形し、簡略化する。
80x+120y=2420-100＝2320
両辺を10で割ると         　8x＋12y＝232
さらに両辺を４で割ると　　　2x＋3y=58・・・（2）´
（1）を変形すると　y=24－x・・・（1）´

（1）´を（2）´に代入すると、
2x＋3(24－x)＝58
2x＋72－3x=58
－x＝58-72＝－14
x=14    よってｙ＝10
ゼリーは14個である。
（プリンは10個）

解法１と解法２は最後はｘに関する式の扱いは全く同じなので、同じ計算になることがわかる。すると解法１（連立方程式を使わず、一次方程式だけで解く）ほうが、式が最初から１つになるので容易である。つまりゼリーｘ個とした場合、プリンが（24－x)個と示されることに気づけば、連立方程式を作る手間を省くことができる。

高校の合格祝いで、サークルやクラスの友達とゼリーとプリンで、パーティーをすることを楽しみにしながら、勉強しましょう。