2015年前期、千葉県公立高校入試「数学」第5問(数の規則性・格子点)問題・解答・解説
2015年2月12日(木)に実施された、2015年前期、千葉県公立高校「数学」第5問(数の規則性・格子点)の問題・解答・解説です。タイトルの「格子点」の命名は私(朝倉)によるものです。格子点とは、座標上でx座標、y座標とも整数である点のことです。高校入試では時々出題されます。この問題では座標は設定してありませんが、AかBを座標の原点とすると実質は格子点の問題ですので、類題との関連性を強調するため、そう命名しました。各小問の配点と千葉県教育委員会が発表した正答率(無答率)も付記しました。
第5問(数の規則性・格子点)(計15点)
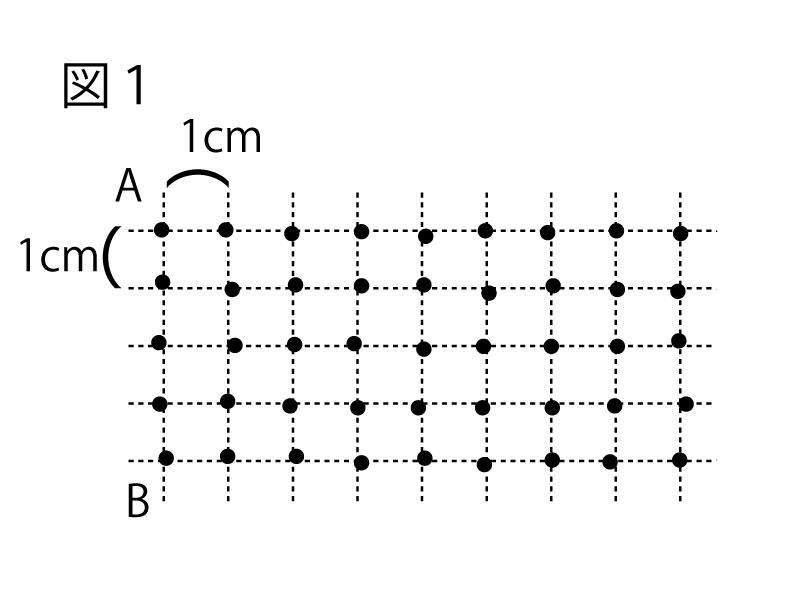
図1のように、1目もりが、縦、横ともに1cmの等しい間隔で線がひかれている方眼紙の、縦軸と横軸の交点に点(●)が打ってある。この点のうちから、2点A、BをAB=4cmとなるようにとる。
さらに、点Cを∠CAB=90°、AC=ncm(nは正の整数)となるようにとり、3点A、B、Cを結んで直角三角形をかいたとき、直角三角形ABCの内部及び周上にある点の個数をNとする。次のはるかさんと先生の会話を読み、(1)~(3)の問いに答えなさい。
はるかさんと先生の会話
先生 :これから、nの値と、直角三角形ABCの内部及び周上にある点の個数Nの関係について考えましょう。
はるか:直角三角形の面積は長方形の半分だから、点の戸数も長方形の半分じゃないですか。
先生 :では、n=5のときで確かめてみましょう。
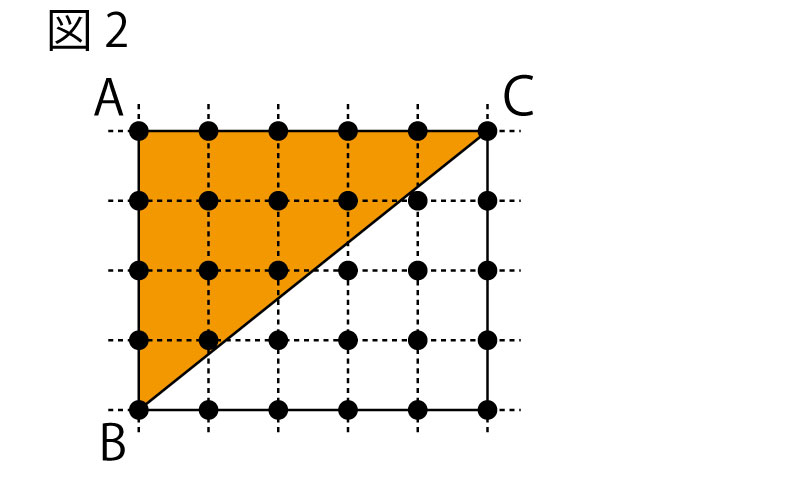
はるか:図2から、n=5のときの直角三角形ABCは、縦が4㎝、横が5㎝の長方形を半分にしたものです。この長方形の内部及び周上にある点の戸数は、5×6で30個ですが、Nを数えたところ16個で、半分ではありませんでした。どうしてですか。
先生 :長方形の点の個数を半分に分けるということは、辺BC上にある点の個数も
半分に分けることになります。でもこの場合、辺BC上にある点は、点B、点C
の2個だけですが、この2個ともNに含まれますよね。
はるか:なるほど、辺BC上にある点の個数がNを求める鍵なんですね。
先生 :では、n=6のとき、辺BC上にある点の個数は何個ですか。
はるか: (ア) 個(2点)(正答率45.9%(無答率3.9%))です。
先生 :それでは、nが他の値の場合についても調べてみましょう。
はるか:nが8までの場合について、辺BC上にある点の個数を書き出したところ、
(イ) 通りしな出てきませんでした。
先生 :nが8より大きい場合を書き出しても、8までと同じ規則性で並ぶので、
辺BC上にある点の個数は、全部で (イ) 通り(2点)(正答率38.4%(無答率3.9%))でいいんですよ。
はるか:そうすると、nがどんな値の場合でも辺BC上にある点の個数が
いくつになるかわかりますね。
先生 :その通りです。辺BC上にある点の個数がわかれば、Nを求めることができます。
n=8のときは、辺BC上にある点は (ウ) 個(2点)(正答率50.0%(無答率10.2%))で、
Nは (エ) 個(2点)(正答率43.4%(無答率12.4%))になります。
(1)会話中の (ア) ~ (エ) に入る数をそれぞれ書きなさい。
(2)辺BC上にある点の個数が最も多くなる場合のnとNの関係について考える。
このとき、Nを、nを使った式で表しなさい。(4点)(正答率6.0%(無答率47.8%))
(3)辺BC上にある点の個数が最も少なくなる場合のnとNの関係について考える。
このとき、N=186であるようなnの値を求めなさい。(3点)(正答率3.2%(無答率58.1%))
[next_p]