2015年前期、千葉県公立高校入試「数学」第4問（図形の証明）問題・解答・解説

2019年8月2日 2019年8月24日

asakura

2015年2月12日（木）に実施された千葉県公立高校入試「数学」第4問（図形の証明）の問題・解答・解説です。千葉県教育委員会が発表した正答率（無答率）も付記しました。

第4問（図形の証明）（計15点）

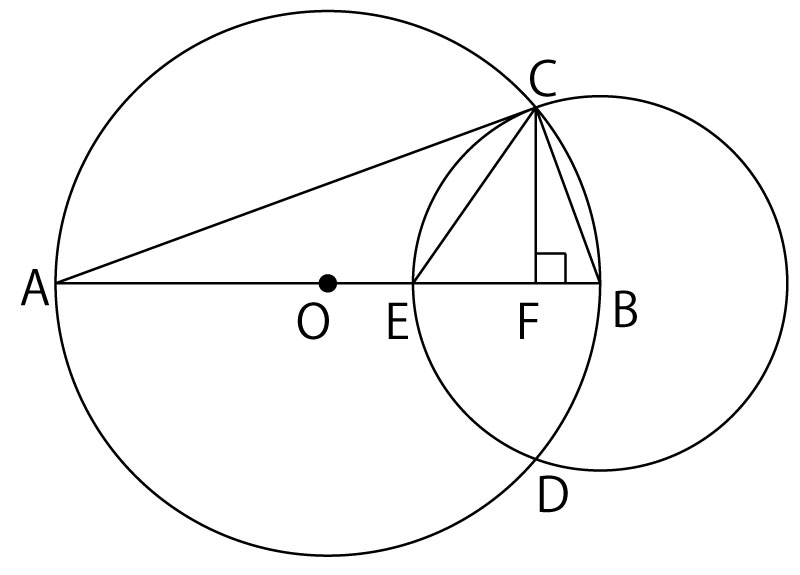
図のように点Ｏを中心とし、線分ABを直径とする円Ｏがある。線分OB上に、2点O,Bと異なる点Eをとり、点Bを中心とし、線分BEを半径とする円Bをかく。２つの円の交点をC、Dとし、点Ｃから線分ABに垂線CFをひく。また、点Cと、点A、点B、点Eをそれぞれ結ぶ。このとき、次の（1）（2）の問いに答えなさい。

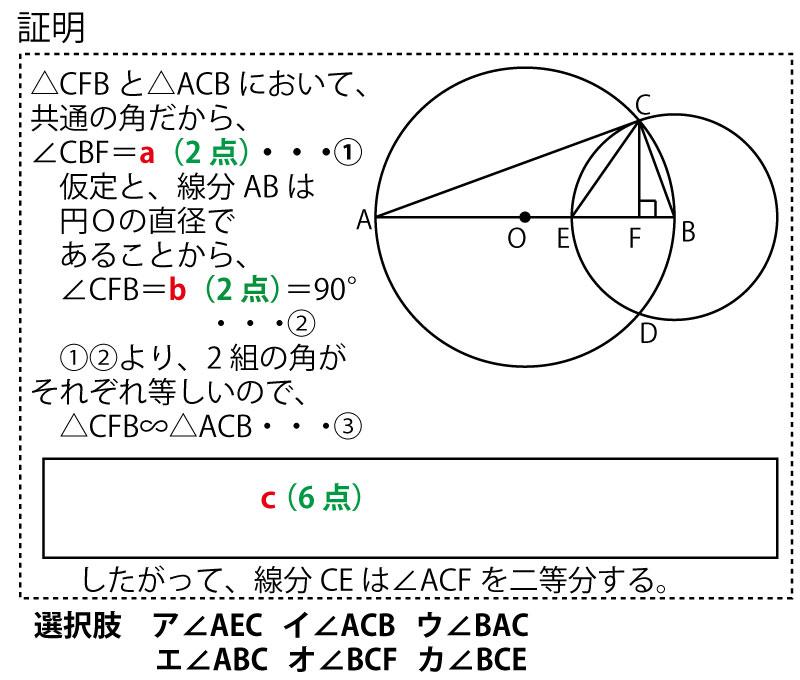
（1）線分CEが∠ACFを二等分することの証明を、の中に途中まで示してある。 a（2点）（正答率87.9%(無答率0.6%))、
b （2点）（正答率87.5%（無答率0.8%))に入る最も適当なものを、あとの選択肢のア～カの中から１つずつ選び、符号で答えなさい。また、
ｃ（6点）（6点評価1.9%、3点評価0.9%（無答率72.2%)）には証明の続きを書き、証明を完成させよ。ただし　の中のに
示されている関係を使う場合、番号を用いてもかまわないものとする。