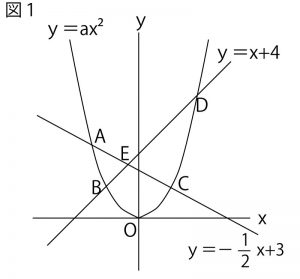
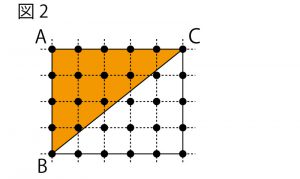
2015年前期、千葉県公立高校入試「数学」第4問（図形の証明）問題・解答・解説

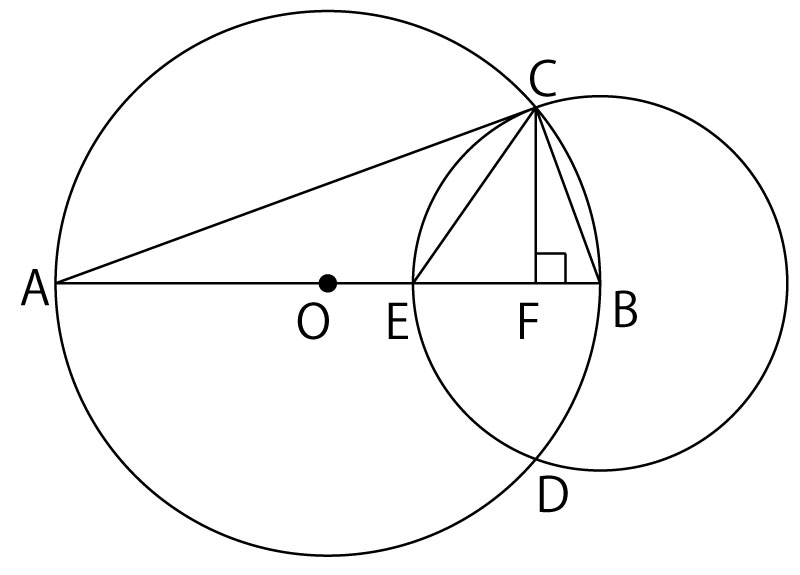
●解説

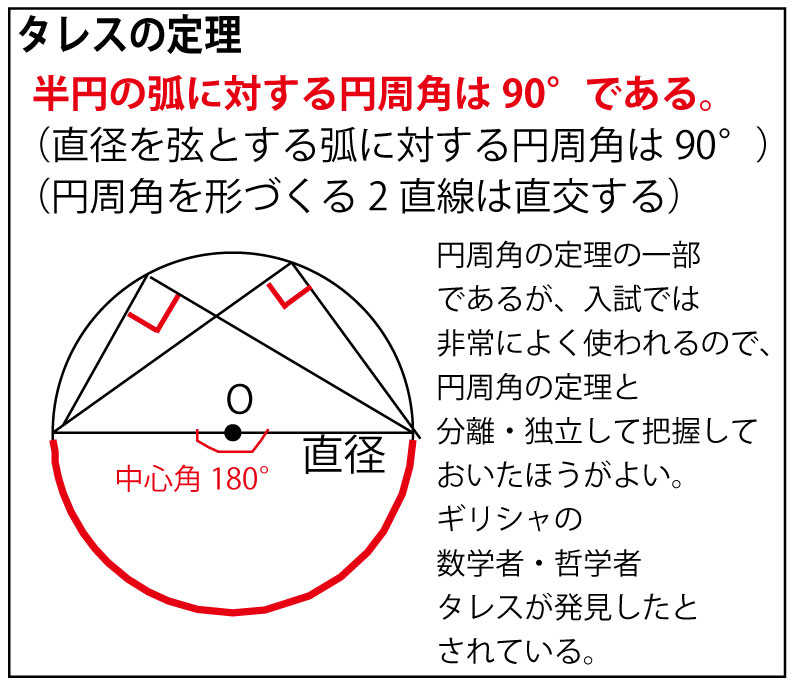
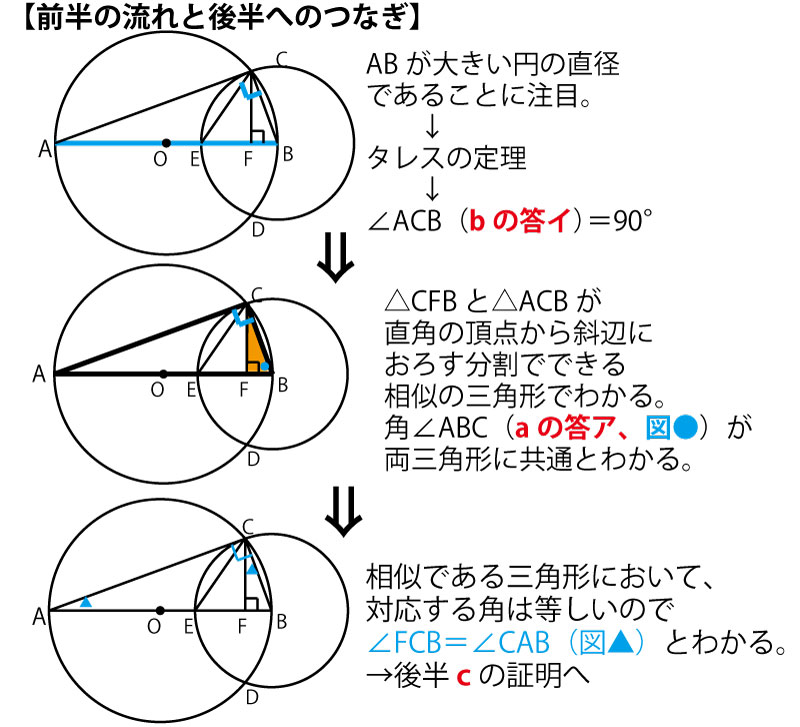
円に内接する図形が多く出てくるので、まずは円周角の定理とタレスの定理の活用を考える。円周角の定理は同じ弧に対する円周角に相当する部分がないので使えない。一方、タレスの定理から、ABが円Oの直径であることに気づくと∠ACF＝90°とわかる。
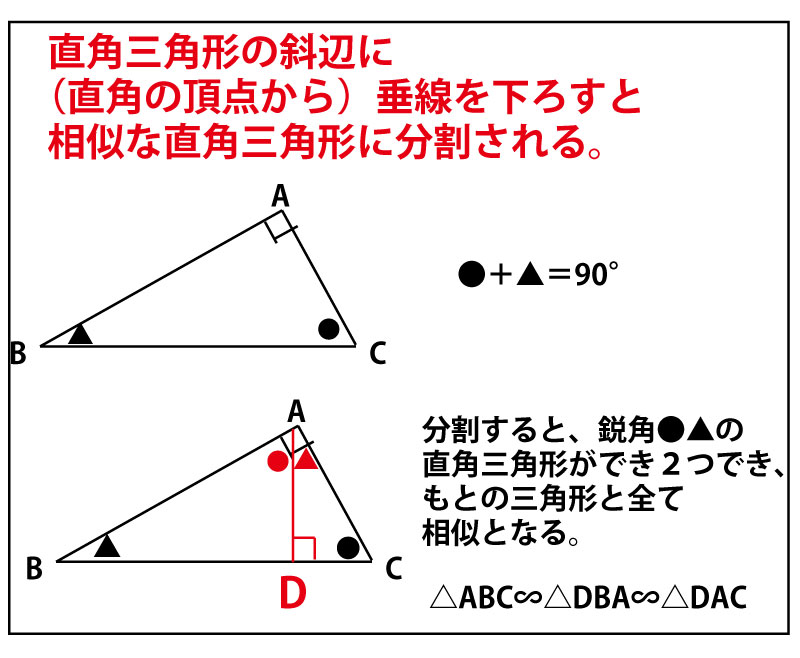
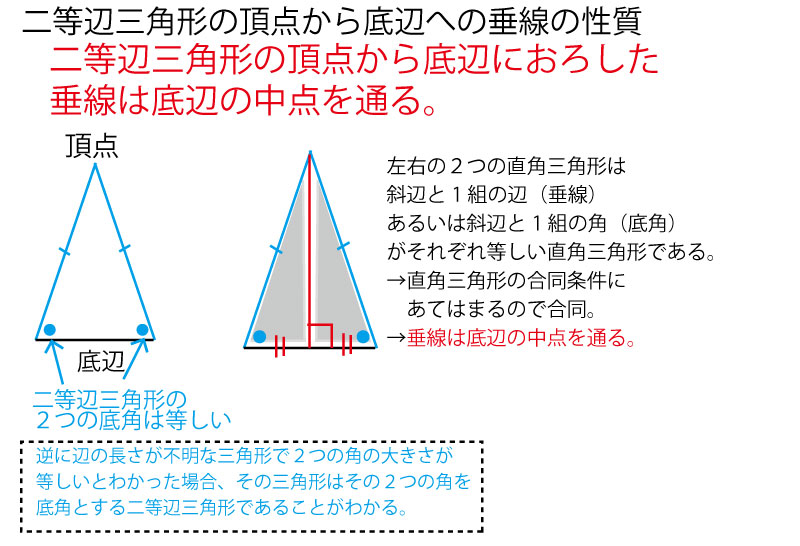
次の直角三角形の直角の頂点から斜辺の下した垂線で分割される相似な三角形の関係を使う。この関係はよくつかわれる。図の中でこの形が出てきた時は必ず使うといっていいぐらいの重要な関係である。この問題でも前半で証明する手段の△CFB∽△ACBはこの関係である。

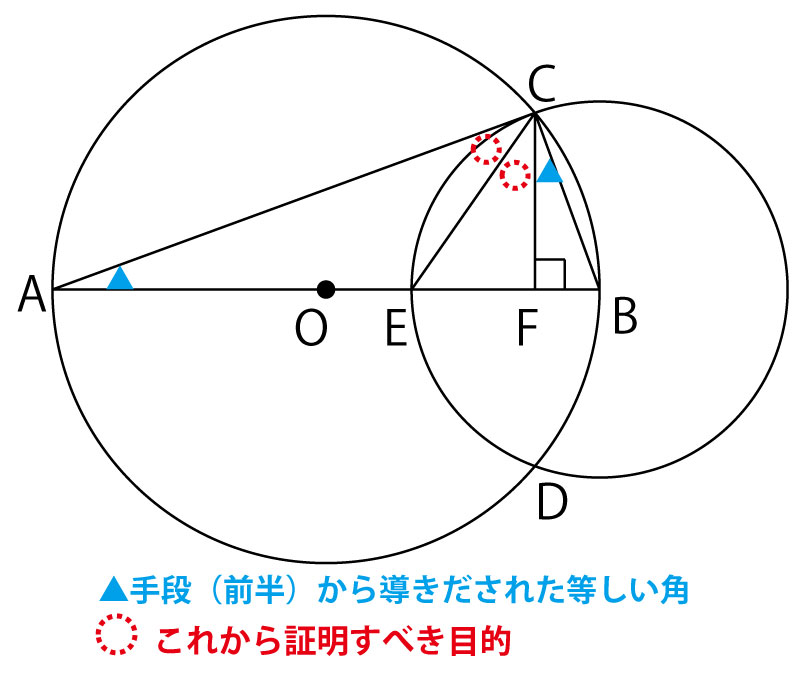
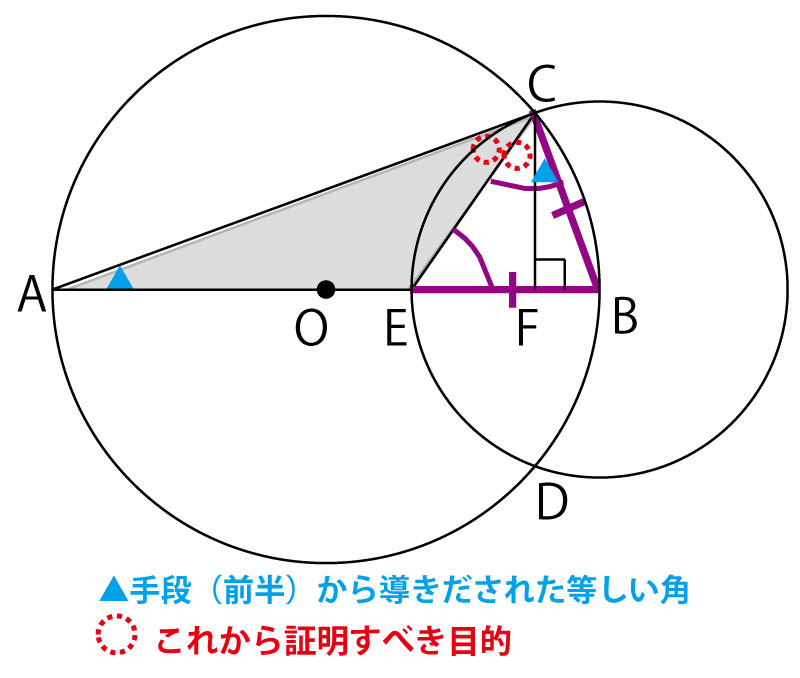
後半ｃの証明を考えていこう。目的は以下の赤点線の部分です。点線で示したのは、まだ証明されていなくて、これから証明すべき目的であることを示すイメージです。

これだけ円が描いてあり、図形が内接しているので、円周角の定理の活用を考えるが、同じ円周角に相当するものが見当たらない。

そこで発想を変え、BEとBCが小さい円の半径であり、同じ円の半径の長さは等しいので、CE＝BCで△BECが二等辺三角形であることに注目する。二等辺三角形の底角は等しいので、∠BCE＝∠BECとなる。

次に灰色の三角形△EACに注目すると、外角は隣り合わない内角の和に等しいことを活用して証明する。
以下、照明（ｃ）の部分の答えを、図の流れと照らし合わせやすいように図の中の記号を書きこんだのでじっくり確認してほしい。

ｃの答

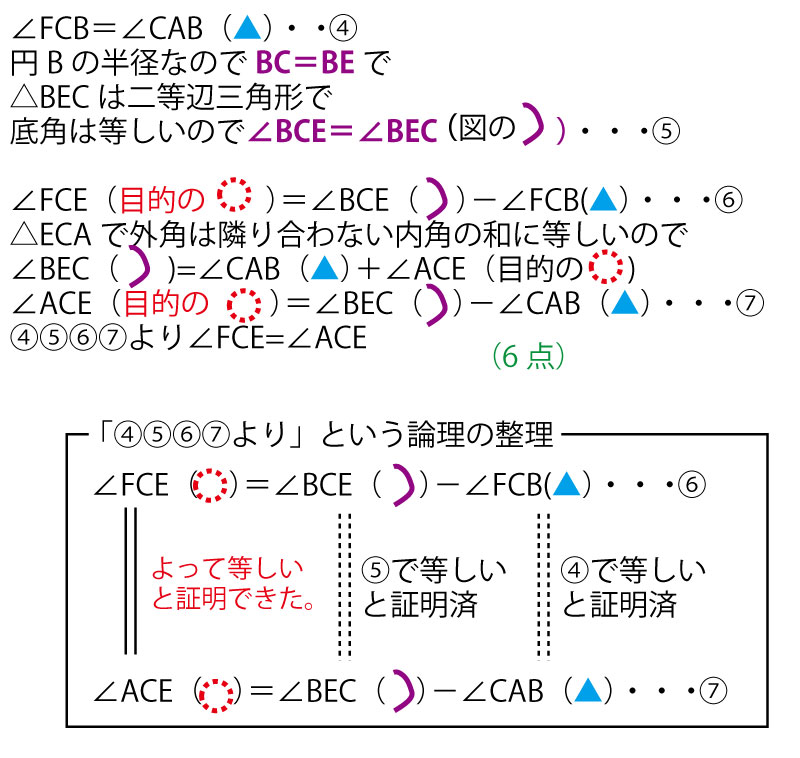
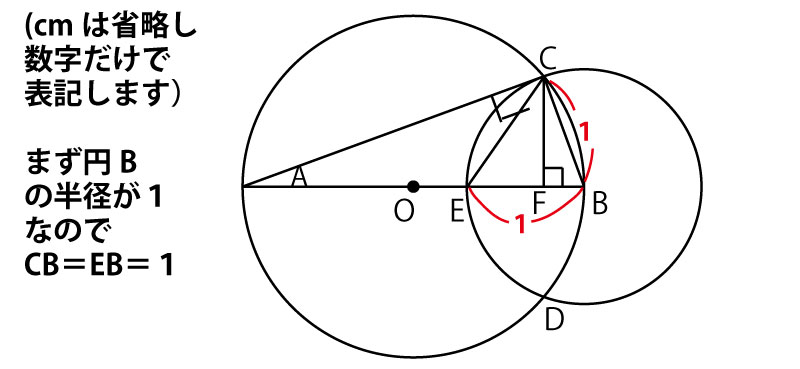
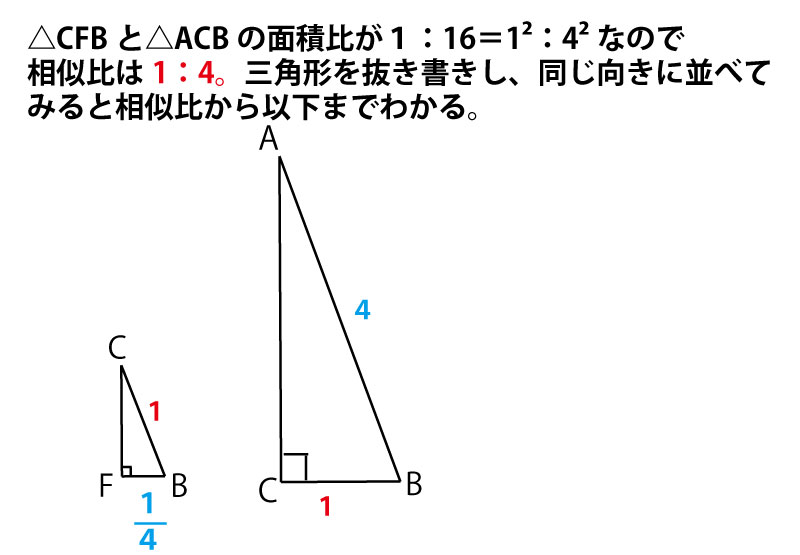
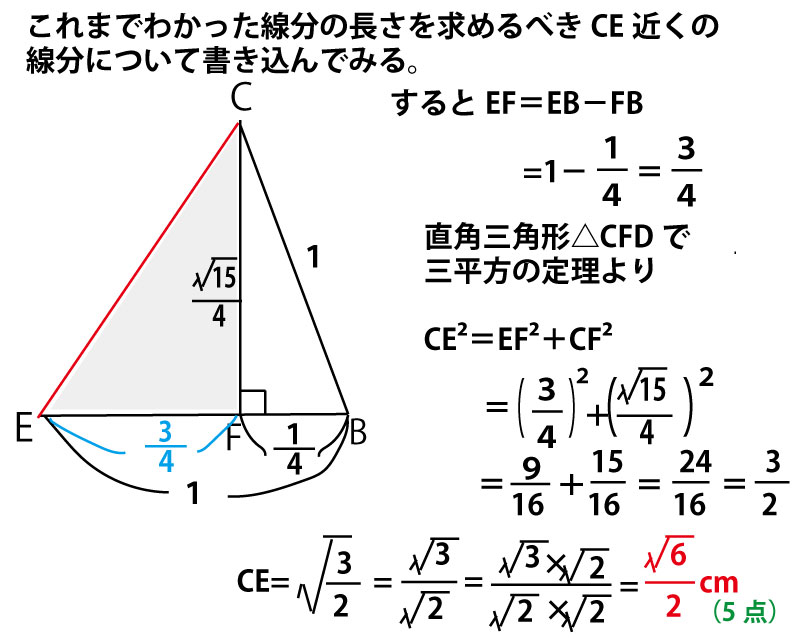
（2）解説

（千葉県の問題では、解答欄に単位cmが印刷してあるので忘れることはない。しかし、他の試験では単位を書き忘れると減点されることもありうるので単位を忘れないこと。）