2019年大学入試センター試験数学IA第2問（2）（統計）（配点15点）問題・解答・解説

入試問題自体は白黒ですが、せっかくの画面上ですので一部カラーにしました。また図は私が模写したものです。点や線の位置に微妙にずれがあるものもありますが、問題を解く上では大丈夫な程度です。

2019年センター数学ⅠA[２]（統計・データ分析）（配点15点）

全国各地の気象台が観測した「ソメイヨシノ（桜の種類）の開花日」を、「モンシロチョウの初見日（初めて観測した日）」、「ツバメの初見日」などの日付を気象庁が発表している。気象庁発表の日付は普通の月日形式であるが、この問題では該当する年の1月1日を「１」とし、12月31日を「365」（うるう年の場合は「366」）とする「年間通し日」に変更している。例えば、2月3日は、1月31日の「31」に2月3日の３を加えた「34」となる。

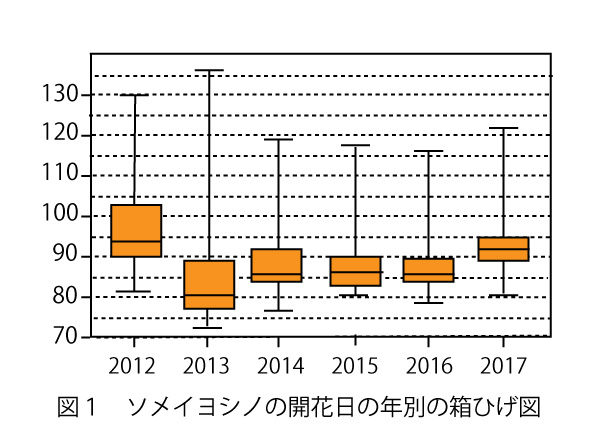
（1）図１は全国48地点で観測しているソメイヨシノの2012年から2017年までの6年間の開花日を、年ごとに箱ひげ図にして並べたものである。

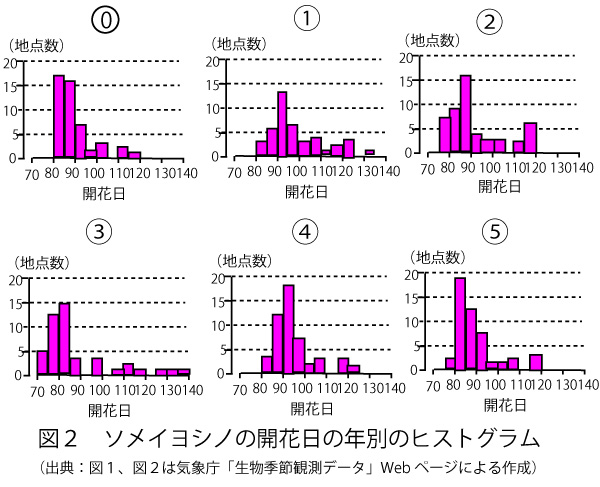
図１はソメイヨシノの開花日の年ごとのヒストグラムである。ただし、順番は年の順に並んでいるとは限らない。なお、ヒストグラムの各階級の区間は、左側の数値を含む、右側の数値を含まない。

次のソ、タに当てはまるものを、図２ののうちから一つずつ選べ。

・2013年のヒストグラムはソである。
・2017年のヒストグラムはタである。

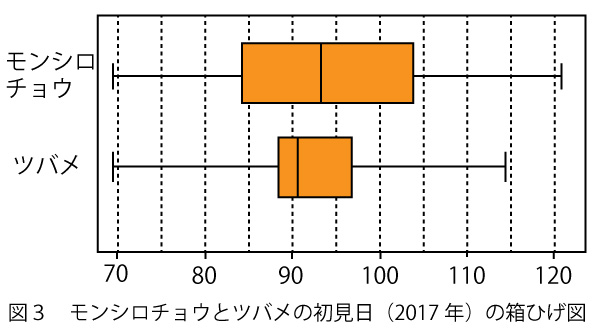
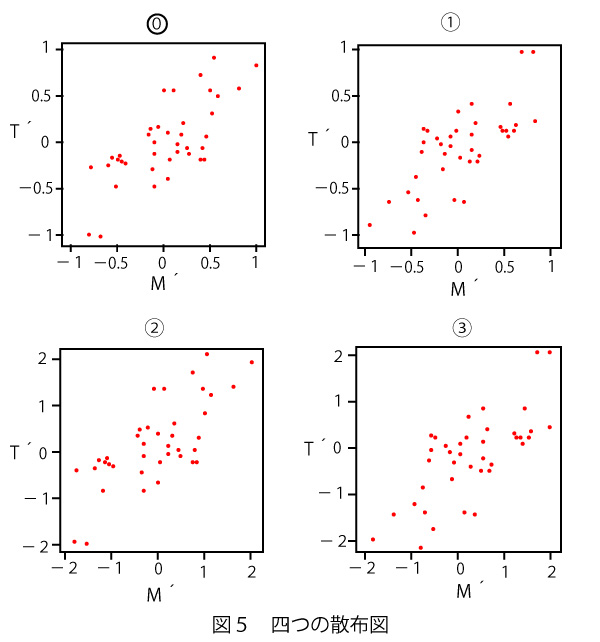
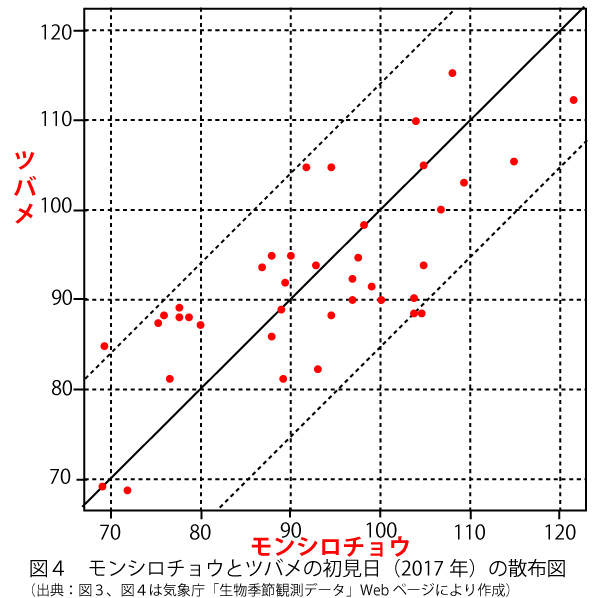
（2）図３と図４は、モンシロチョウとツバメの両方を観測している41地点における、2017年の初見日の箱ひげ図と散布図である。散布図の点には重なった点が2点ある。なお、散布図には原点を通り傾き１の直線（実線）、切片が−15および15で傾きが１の2本の直線（破線）を付加している。
次のチ、ツに当てはまるものを、下ののうちから一つずつ選べ、ただし、解答の順序は問わない。

図３、図４から読み取れることとして正しくないものは、チ、ツである。
モンシロチョウの初見日の最小値はツバメの初見日の最小値と同じである。
モンシロチョウの初見日の最大値はツバメの初見日の最大値より大きい。
モンシロチョウの初見日の中央値の中央値はツバメの初見日の中央値より大きい。
モンシロチョウの初見日の四分位範囲はツバメの初見日の四分位範囲の3倍より小さい。
モンシロチョウの初見日の四分位範囲は15日以下である。
ツバメの初見日の四分位範囲は15日以下である。
モンシロチョウとツバメの初見日が同じ所が少なくとも４地点ある。
同一地点でのモンシロチョウの初見日とツバメの初見日の差は15日以下である。

[next_p]