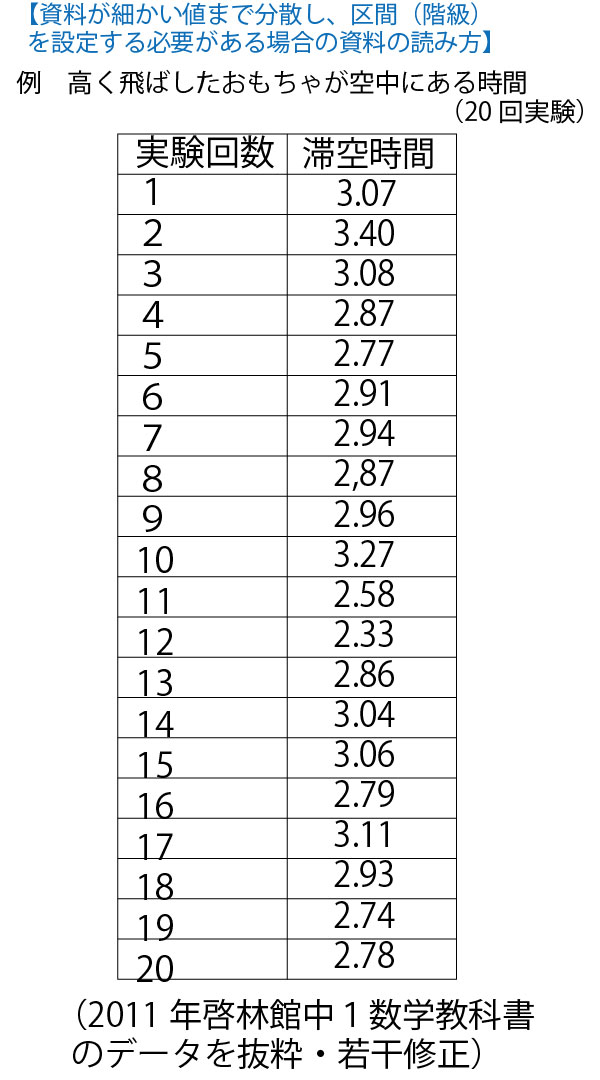
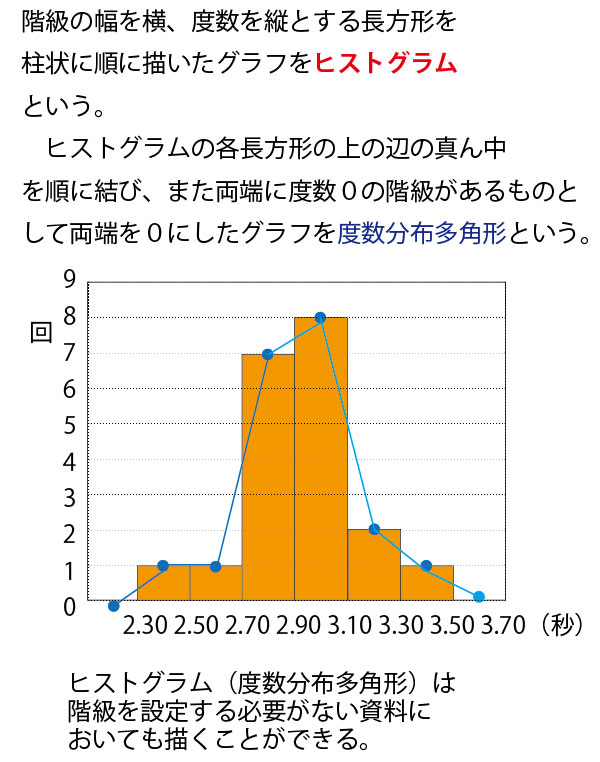
2019年大学入試センター試験数学IA第2問（2）（統計）（配点15点）問題・解答・解説

解答　ソ（3点）　タ（3点）　チ・ツ（2点×２）テ（1点）　ト（1点）ナ（1点）　ニ（2点）

解説（1）（ソタ）

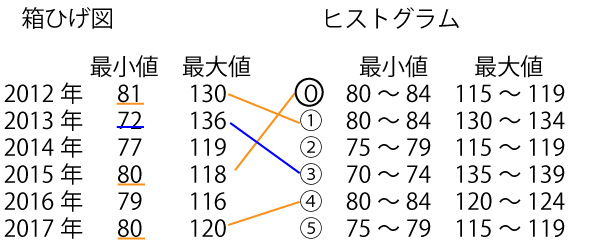
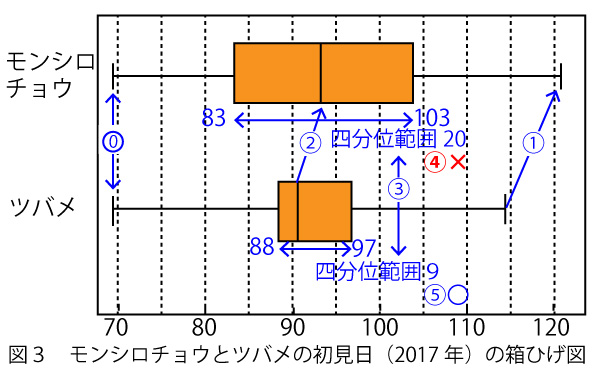
設問では箱ひげ図が縦になっているが、ヒストグラムと合わせて横向きに考えてみる。

 

まずは箱ひげ図やヒストグラムの概形を分析しなくてもすぐわかる「最小値・最大値」が一致しているかで分類してみる。ヒストグラムについては、設問に
「ヒストグラムの各階級の区間は、左側の数値を含む、右側の数値を含まない」
と書かれていることを見落とさすに、読むと以下の通りとなる。

 

図の青線のように最小値が70～74の範囲は2013年しなないので、2013年がであるとすぐわかる。（ソ）（3点）。
次に図のオレンジ選のように最小値が80～84の範囲は、2012・2015・2017年の3年があるが、それぞれ最大値の値から特定できる。よって2017年はである。（タ）（3点）
このように本設問（2013・1017年）は最大値・最小値のみで判別できるが、そうでない場合は、中央値・Q１、Q2などグラフの概形も考慮に入れて考える。

解説（2）（チツ）

下の図の通り、が正しく、が正しくない。すなわち選択すべき答である。（2点×２）

解説（３）（テトナニ）

偏差の平均は以下のように０となる。変換したX´の場合も分子部分の和が偏差の平均なので０となる。よってテ（1点）ト（1点）

ナの答えは以下の計算のようにとなる。（1点）

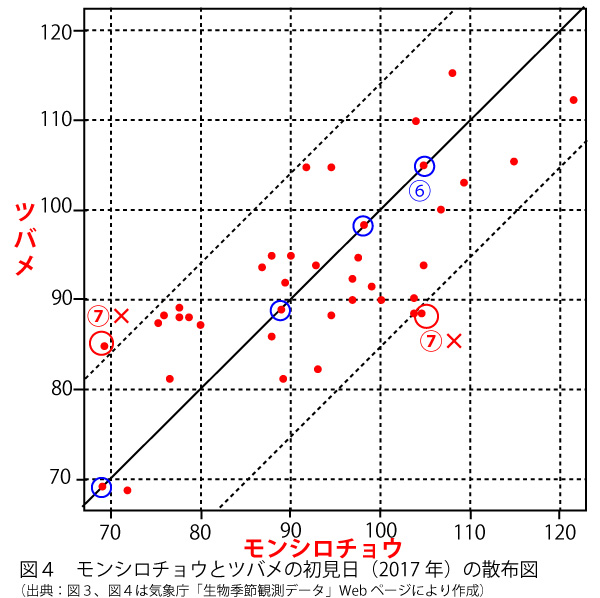
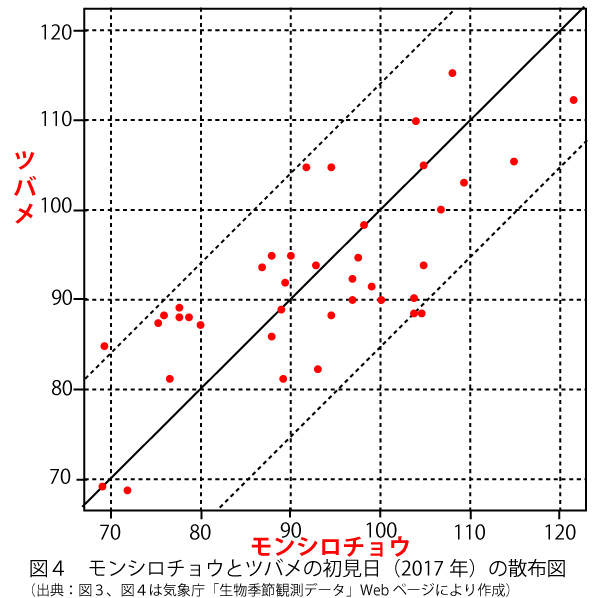
M´、T´は偏差を標準偏差で割る同様な計算でM、Tから求められるので、両者の散布図は元の散布図（図４）と同じ点の配置となるはずである。よってか。

この図で０は平均の値を示し、平均から標準偏差だけ離れた点は−１と１の値となる。データの中には標準偏差以上の偏差のものもあるはずなので（2点）

 

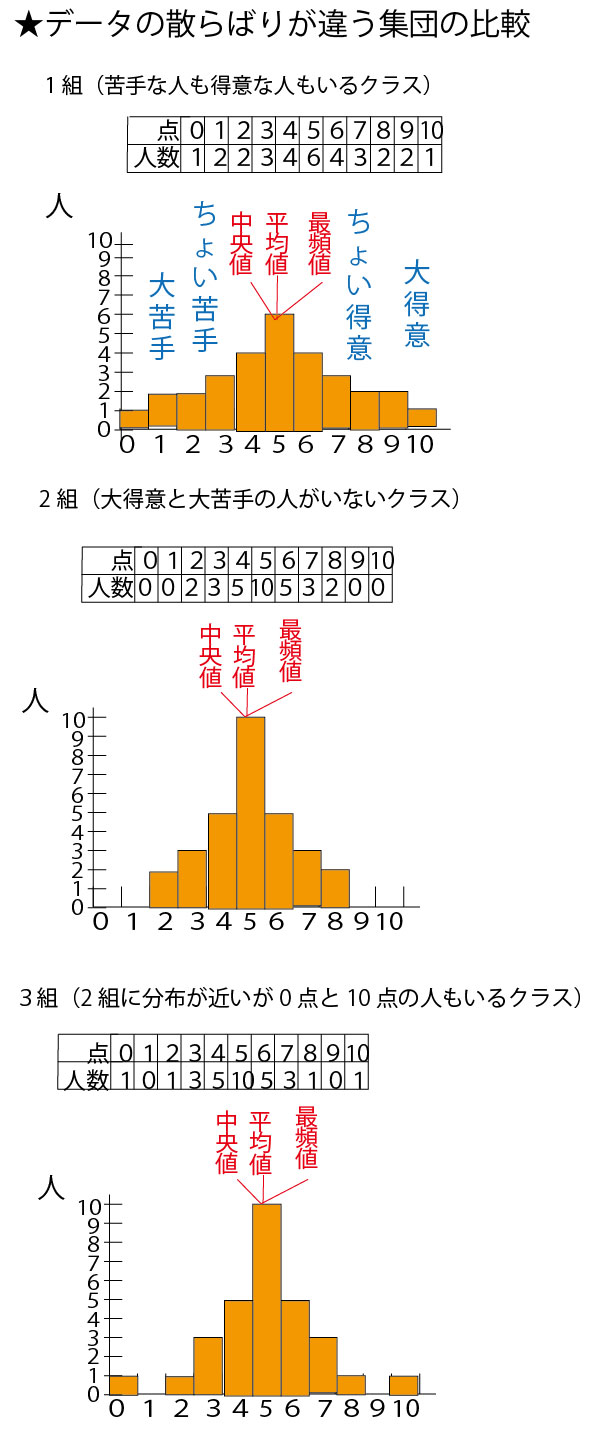
★【中学（中１「資料の整理」）】分野のまとめ

★高校数Ⅰ（データの分析）分野のまとめ。

中学１年で学ぶ「資料の整理」の発展編であり、この学問分野を統計学という。

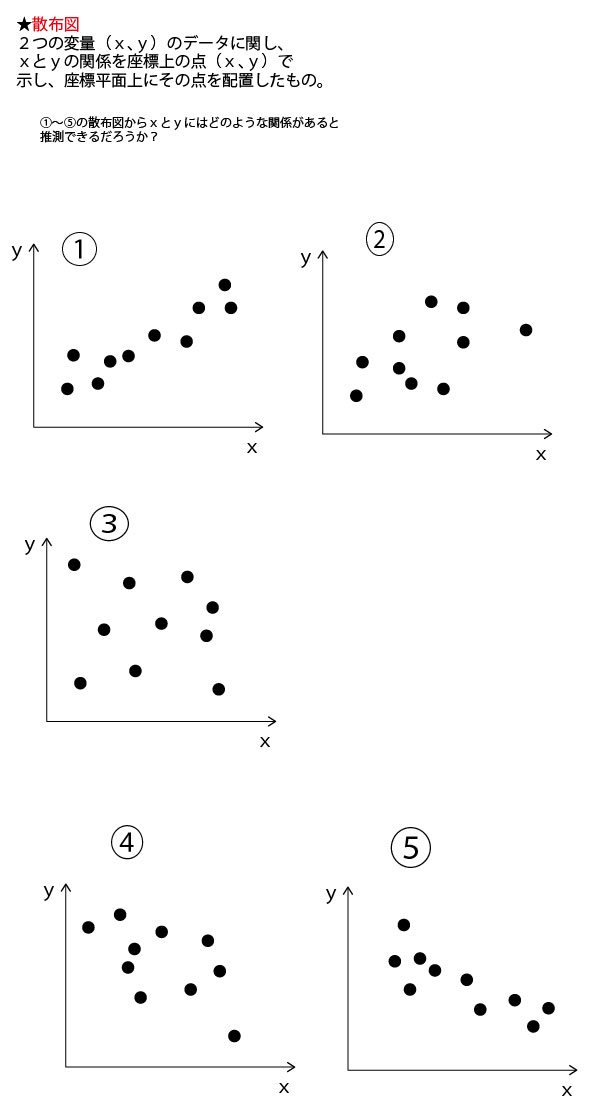
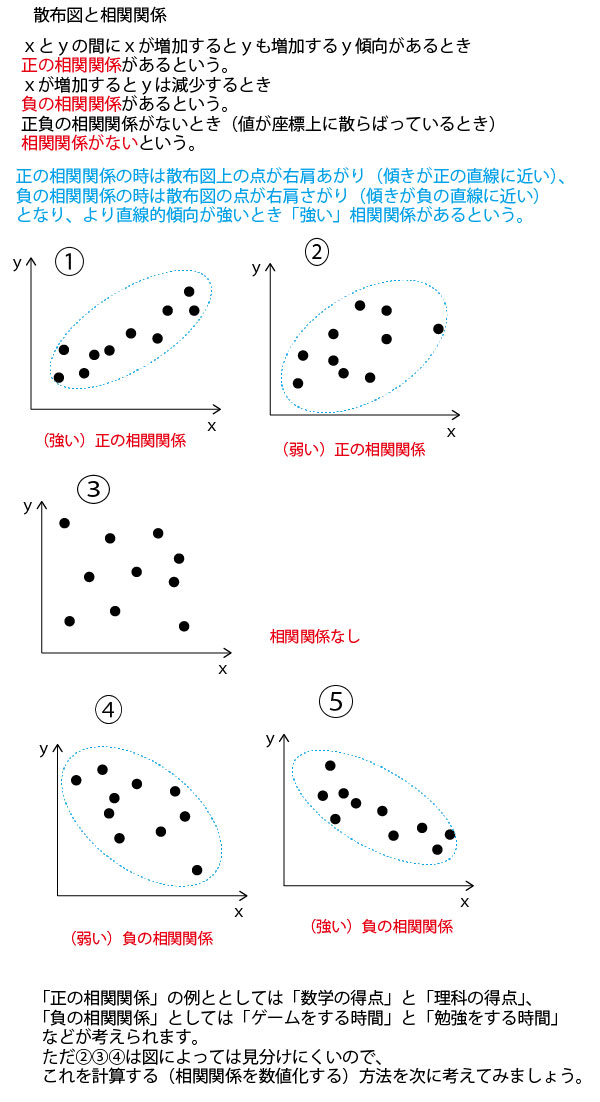
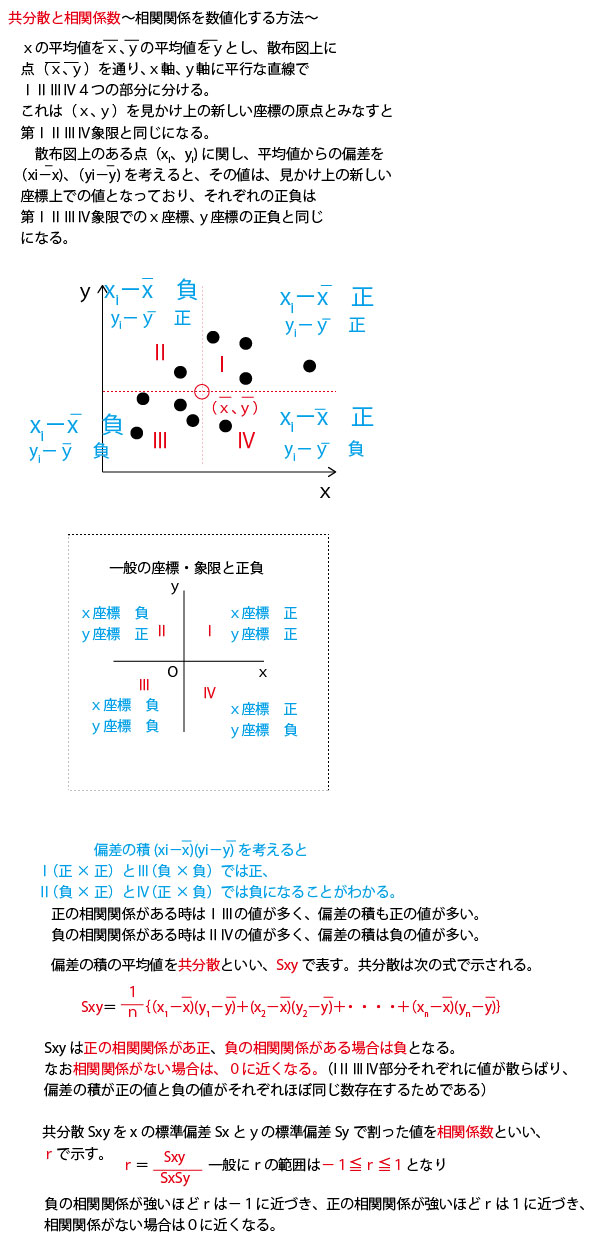
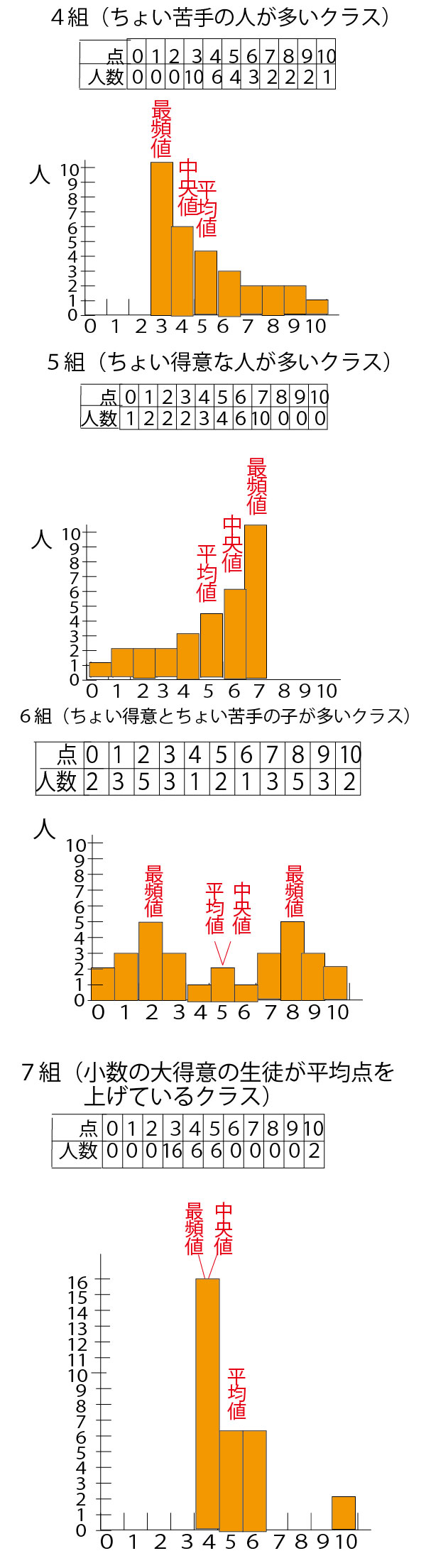
具体例として、数学の小テスト（10点満点）の平均点がいずれも5点が分布が異なる30人の７クラス（１組～7組）を例に考えていこう。

 

 

 

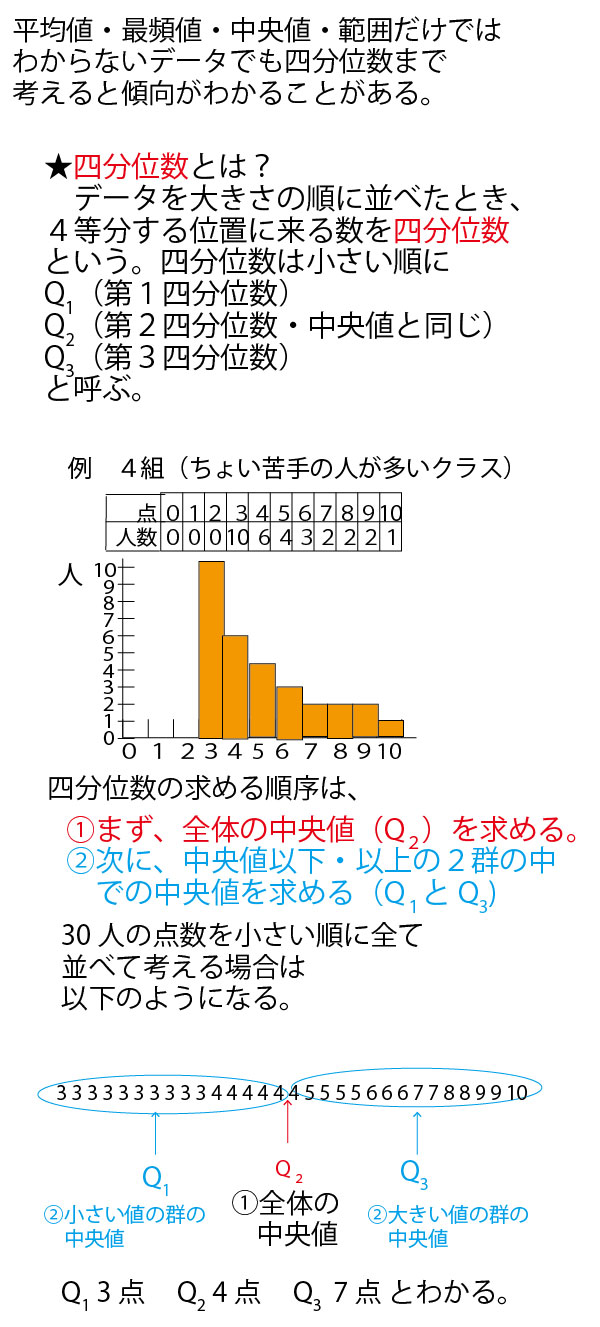
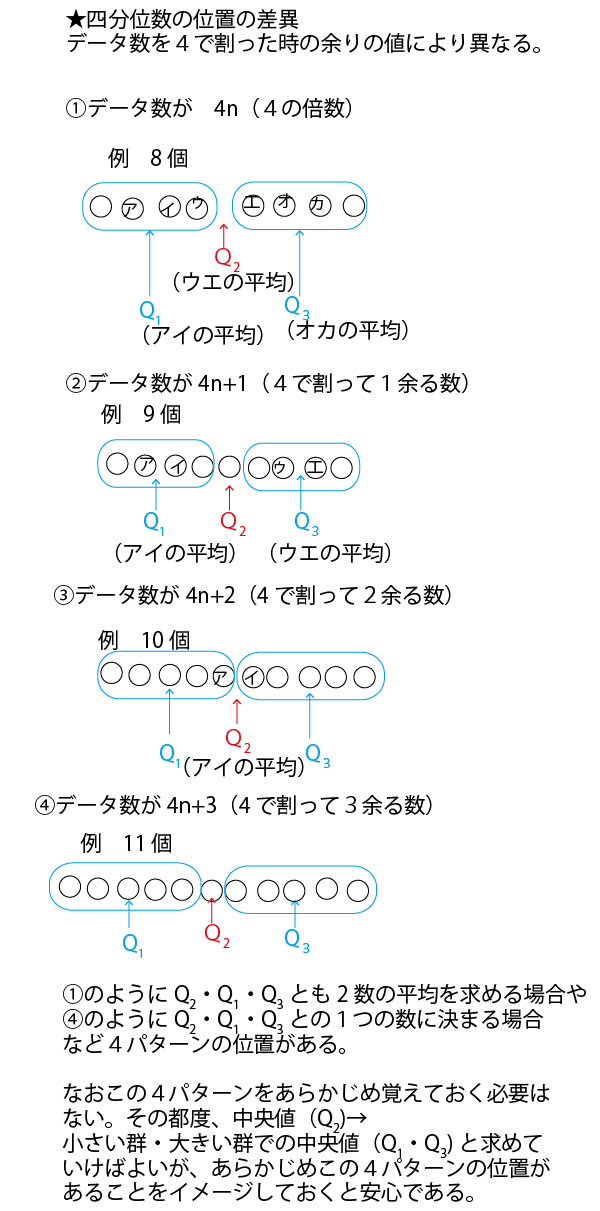
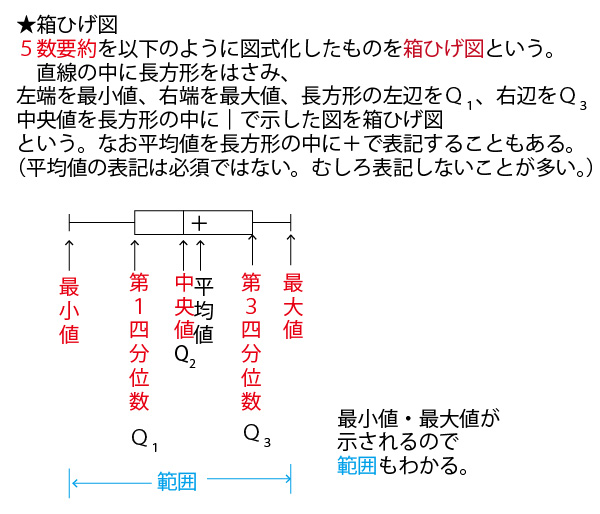
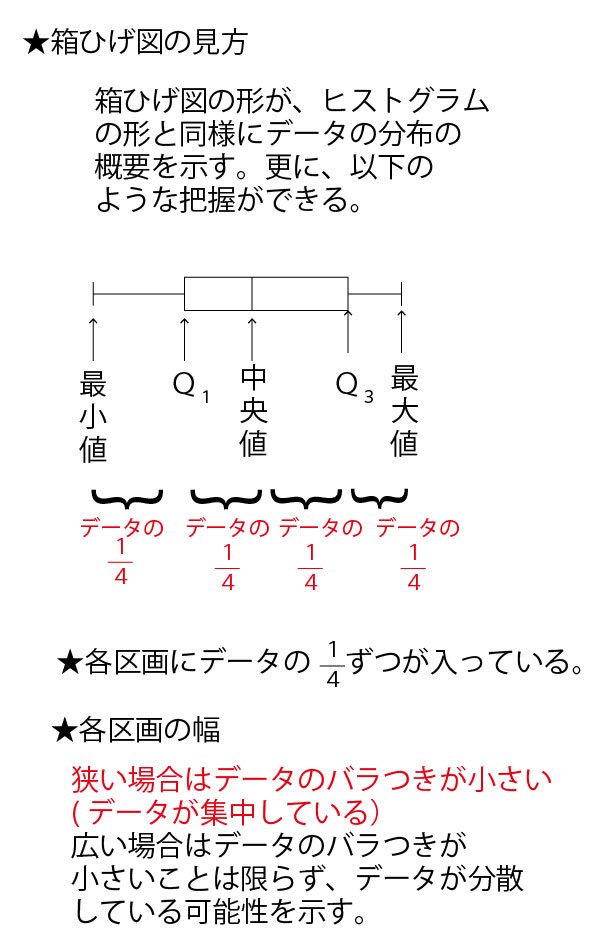
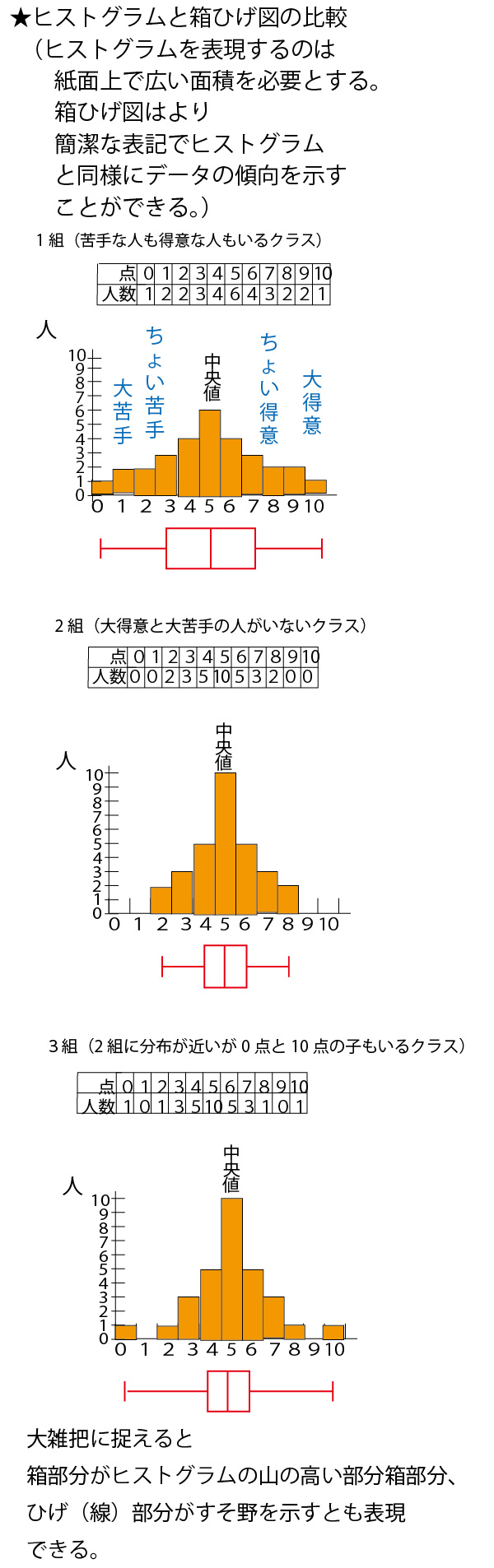
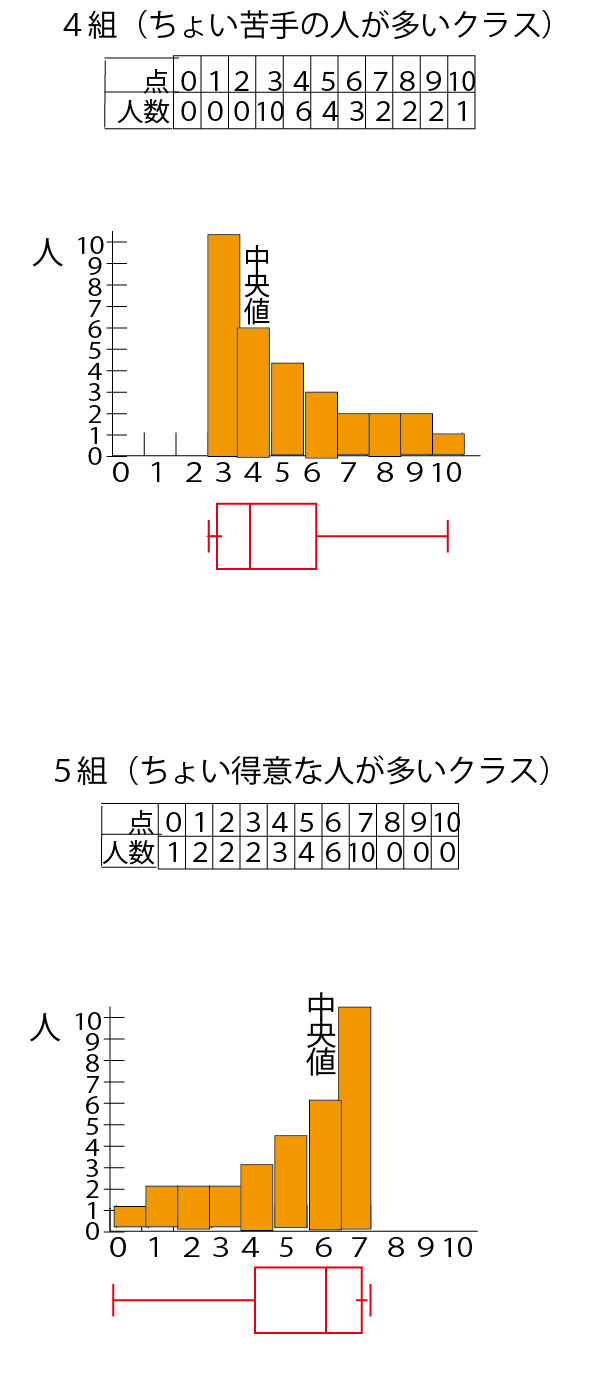
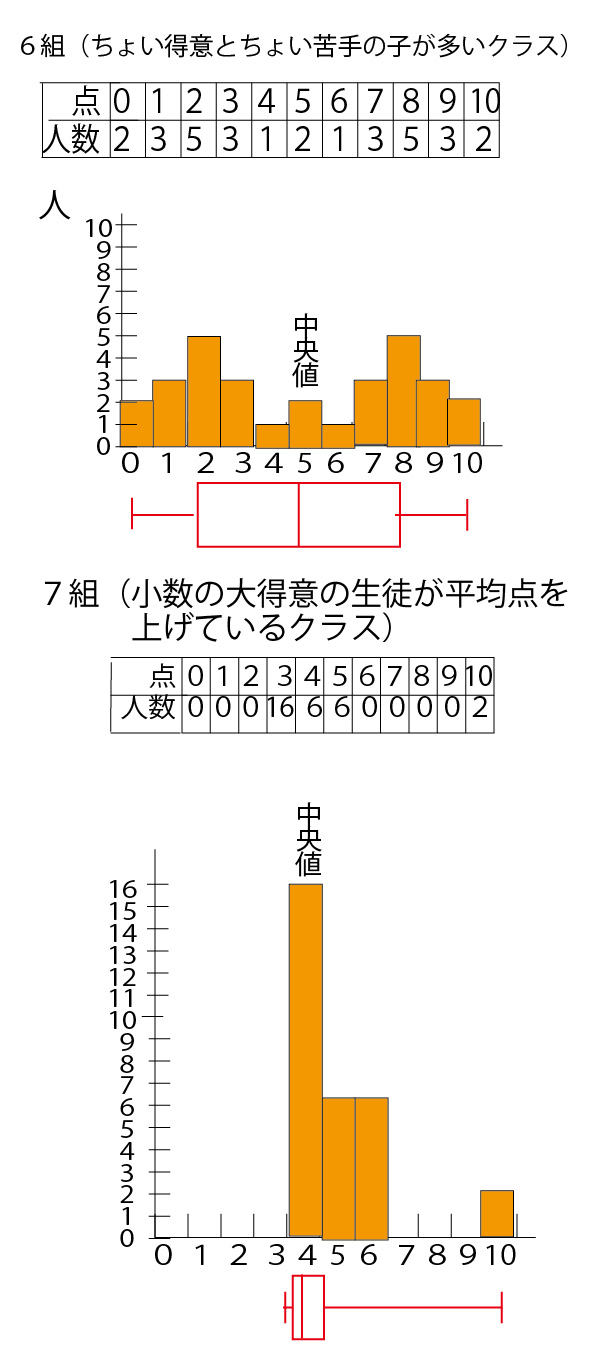
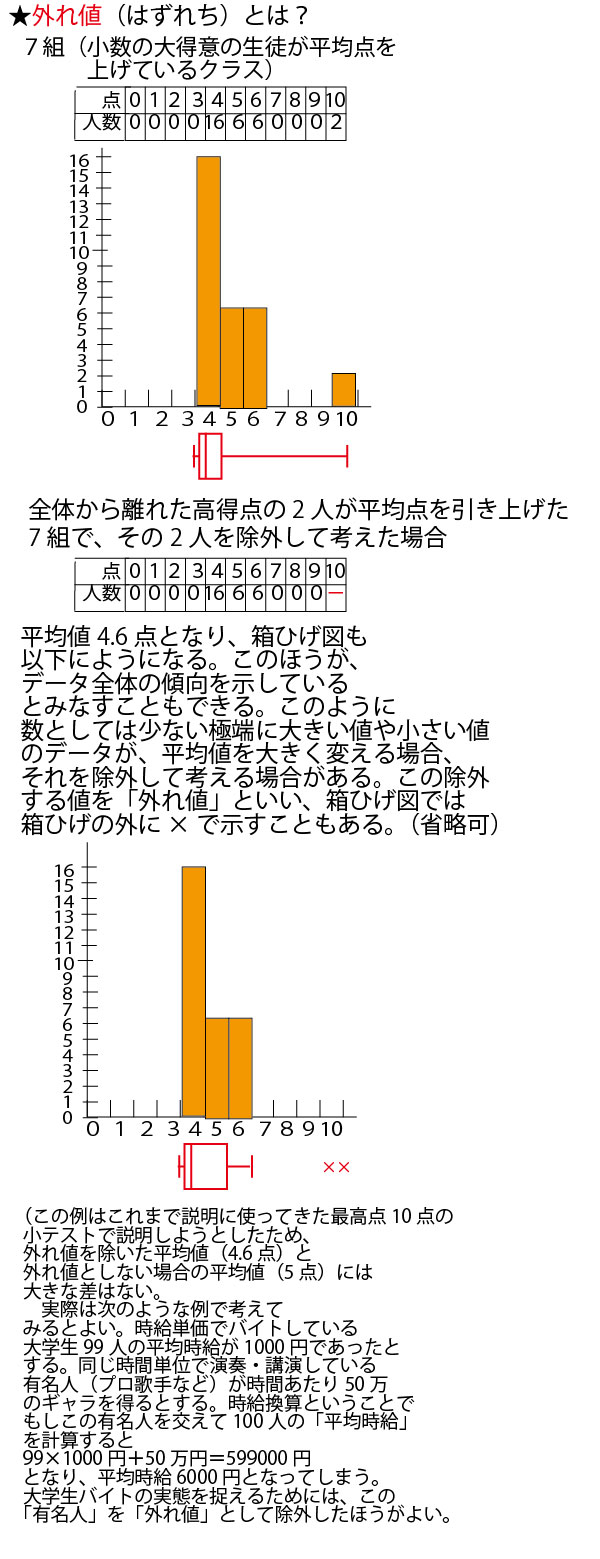
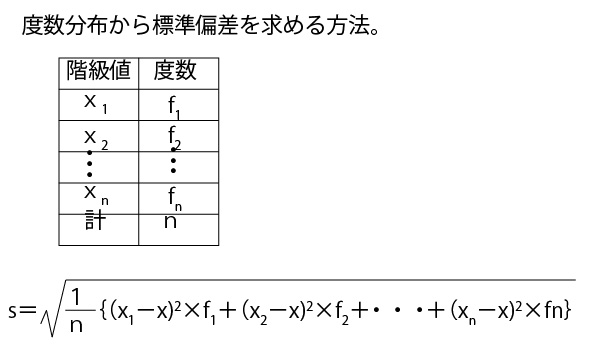
分散・標準偏差に関しては、最初に考えるのは30人クラスでは大きすぎて考えにくいので、まずは、平均点がいずれも5点となる5人組の５班（１班～５班）を例に考えていこう。