2021年大学入試共通テスト「数IA」第2問［１］（短距離走におけるストライド・ピッチ・タイムの関係）（15点配点）問題・解答・解説

2021年1月31日 2021年2月13日

asakura

2021年1月　予備校講師、「円」「三角形」「図形の証明」著者、船橋市議　朝倉幹晴

2021年1月17日（日）に実施された大学入試共通テスト数学IA第2問［1］（ア～ソ）（計15点）の問題・解答・解説です。
本設問は一次関数・二次関数など基本的な問題ですが、現実の短距離走という現実の素材から考えさせているのが特徴です。
同じ第1問でも［2］（統計）（タ～ナ）（計15点）は実質的に別の問題なので、別に解答・解説を作ります。

2021年受験生は２次試験に向けた復習に、2022年以降の受験生は来年の準備にご活用ください。
実際の入試問題は白黒印刷ですが、画面上ですのでカラーを一部使いました。ア～ソには当てはまる数字（０～９）・－（マイナス）・あるいは選択肢の番号を入れる形で答えてください。

第2問［１］

陸上競技の短距離100ｍ走では、100ｍを走るのにかかる時間（以下、タイムと呼ぶ）は、一歩あたりの進む距離（以下、ストライドと呼ぶ）と1秒あたりの歩数（以下、ピッチと呼ぶ）に関係がある。

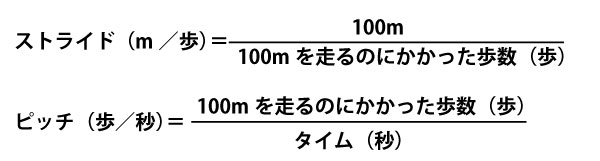
ストライドとピッチはそれぞれ以下の式で与えられる。

ただし、100ｍを走るのにかかった歩数は、最後の１歩がゴールラインをまたぐこともあるので、小数で表される。以下、単位は必要のない限り省略する。
例えば、タイムが10.81で、そのときの歩数が48.5であったとき、ストライドは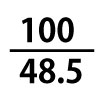より約2.06、ピッチはより約4.49である。

なお、小数の形で解答する場合は、解答上の注意にあるように、指定された桁数の一つ下の桁を四捨五入して答えよ。また、必要に応じて、指定された桁までにマークせよ。

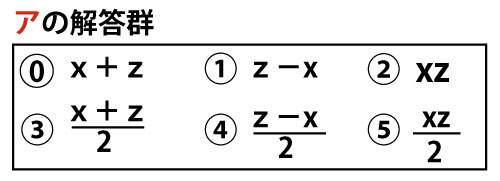
（1）ストライドをｘ、ピッチをｚとおく。ピッチは１秒あたりの歩数、ストライドは1歩あたりの進む距離なので、1秒あたりの進む距離すなわち平均速度は、ｘとｚを用いて、ア（ｍ／秒）と表される。
これより、タイムと、ストライド、ピッチとの関係は

と表されるので、ア（3点）が最大になるときにタイムが最もよくなる。ただし、タイムがよくなるとは、タイムの値が小さくなることである。

（2）男子短距離100ｍ走の選手である太郎さんは、に着目して、タイムが最もよくなるストライドとピッチを考えることにした。
次の表は、太郎さんが練習で100ｍを３回走ったときのストライドとピッチのデータである。

また、ストライドとピッチにはそれぞれ限界がある。太郎さんの場合、ストライドの最大値は2.40、ピッチの最大値は4.80である。
太郎さんは、上の表から、ストライドが0.05大きくなるとピッチが0.1小さくなるという関係があると考えて、ピッチがストライドの1次関数として表されると仮定した。このとき、ピッチｚはストライドｘを用いて

（イウ、エオ　3点）

と表される。

が太郎さんのストライドの最大値2.40とピッチの最大値4.80まで成り立つと仮定すると、ｘの値の範囲は次のようになる。

カ.キク≦ｘ≦2.40　　（カキク　2点）

y=アとおく。をｙ＝アに代入することにより、ｙをｘの関数として表すことができる。太郎さんのタイムが最もよくなるストライドとピッチを求めるためには、カ.キク≦ｘ≦2.40の範囲でｙの値を最大にするｘの値を見つければよい。このとき、ｙの値が最大になるのはｘ＝ケ.コサのときである。（ケコサ　3点）

よって、太郎さんのタイムが最もよくなるのは、ストライドがケ.コサのときであり、このとき、ピッチはシ.スセである。（シスセ　2点）
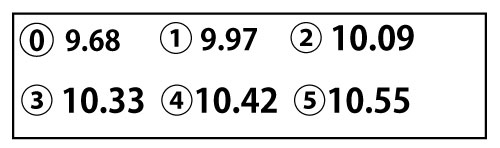
また、このときの太郎さんのタイムは、によりソである。（ソ　2点）