2021年大学入試共通テスト「数学IA」第4問「整数論」（配点20点・選択）問題・解答・解説

2021年２月13日　予備校講師、「円」「三角形」「図形の証明」著者、船橋市議　朝倉幹晴

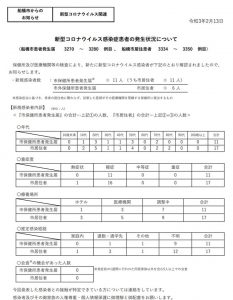
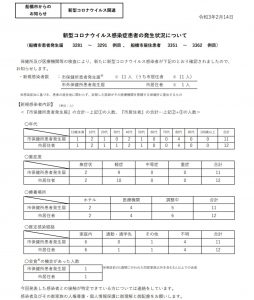
2021年1月17日（日）に実施された大学入試共通テスト数学IA第4問（ア～シ）（計20点、選択、第３～5問（いずれも20点）から2問選択）の問題・解答・解説です。

2021年受験生は２次試験に向けた復習に、2022年以降の受験生は来年の準備にご活用ください。
実際の入試問題は白黒印刷ですが、画面上ですのでカラーを一部使いました。ア～シには当てはまる数字か選択肢の番号を入れる形で答えてください。

第4問（計20点、選択）

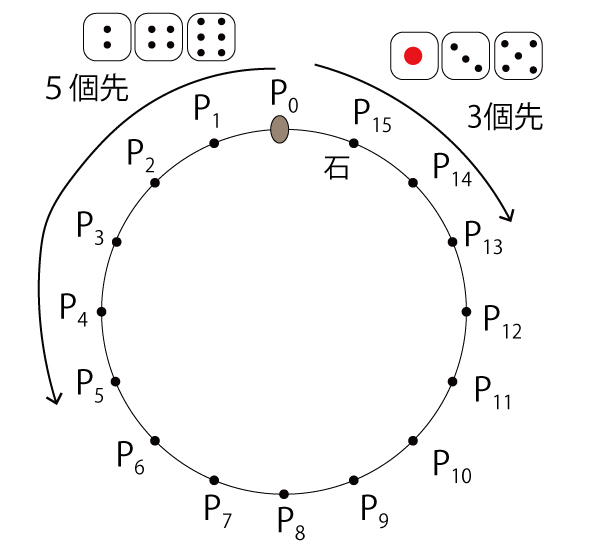
円周上に15個の点P_{0 、}P₁  、・・・、P₁₄が反時計回りに順に並んでいる。最初、点P₀に石がある。さいころを投げて偶数の目が出たら石を反時計回りに5個先の点に移動させ、奇数の目が出たら石を時計回りに３個先の点に移動させる。この操作を繰り返す。例えば、石が点P₅にあるとき、さいころを投げて６の目が出たら石を点P₁₀に移動させる。次に、５の目が出たら点P₇に移動させる。

（1）さいころを5回投げて、偶数の目がア回（1点）、奇数の目がイ回（1点）出れば、点P₀にある石を点P₁に移動させることができる。このとき、ｘ＝ア、ｙ＝イは、不定方程式5x－3y＝１の整数解になっている。

（2）不定方程式
5x－3y＝8
のすべての整数解x、yは、kを整数として
x＝ア×8＋ウk、ｙ＝イ×8＋エk　（ウ、エ両方できて3点）

と表される。の整数解x、yの中で、０≦y＜エを満たすものは
ｘ＝オ（3点）、ｙ＝カ（3点）
である。したがって、さいころをキ回（1点）投げて、偶数の目がオ回、奇数の目がカ回出れば、点P₀にある石を点P₈に移動させることができる。

（3）（2）において、さいころをキ回より少ない回数だけ投げて、点P₀にある石を点P₈に移動させることはできないだろうか。

（＊）石を反時計回りまたは時計回りに15個先の点に移動させると元の点に戻る。

（＊）に注意すると、偶数の目がク回（2点）、奇数の目がケ回（2点）出れば、さいころを投げる回数がコ回（1点）で、点P₀にある石を点P₈に移動させることができる。このとき、コ＜キである。

（4）点P_{1 、}P₂  、・・・、P₁₄のうちから点を一つ選び、点P₀ にある石をさいころを何回か投げてその点に移動させる。そのために必要となる、さいころを投げる最小回数を考える。例えば、さいころを1回だけ投げて点P₀にある石を点P₂へ移動させることはできないが、さいころを2回投げて偶数の目と奇数の目が1回ずつ出れば、点P₀にある石を点P₂へ移動させることができる。したがって、点P₂を選んだ場合には、この最小回数は2回である。
点P_{1 、}P₂  、・・・、P₁₄のうち、この最小回数が最も大きいのは点サ（2点）であり、その最小回数はシ回（3点）である。

サの解答群

[next_p]