2021年、千葉県公立高校入試「数学」第5問（総合問題・配点15点）問題・解答・解説

2021年7月15日　予備校講師・船橋市議　朝倉幹晴

2021年2月の千葉県公立高校入試「数学」の第４問（図形の証明）の問題・解答、そして私（朝倉幹晴）が作成した解説です。千葉県教育委員会が発表した各問の正答率（無答率）も付記しました。ご活用ください。

2021年第5問（15点配点）

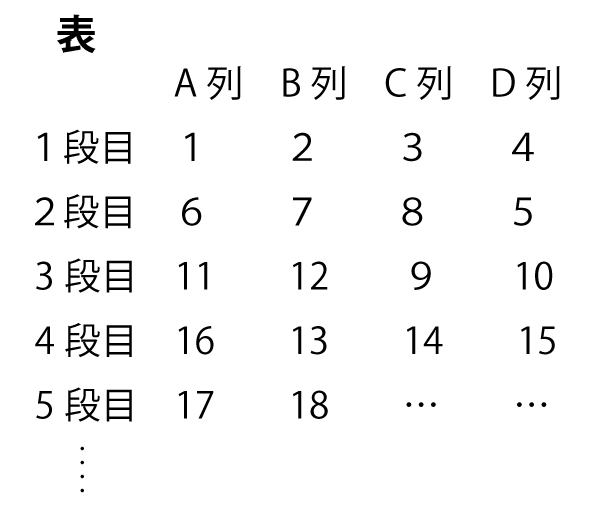
表のように、連続する自然数を１から順に、次の規則にしたがって並べていく。

規則

1段目には、自然数１、２、３、４をA列→B列→C列→D列の順に並べる。

２段目以降は、１つ前の段に並べた自然数に続く、連続する４つの自然数を次の順に並べる。

１つ前の段で最後に並べた自然数が
・D列にあるときは、D列→A列→B列→C列の順
・C列にあるときは、C列→D列→A列→B列の順
・B列にあるときは、B列→C列→D列→A列の順
・A列にあるときは、A列→B列→C列→D列の順

このとき、次の（1）～（3）の問いに答えなさい。
（1）下の説明は、各段に並べた数について述べたものである。ア、イにあてはまる式を書きなさい。

説明
各段の最大の数は４の倍数となっていることから、ｎ段目の最大の数はｎを用いてア（3点）（正答率88.5%（無答率4.0%))と表される。
したがって、ｎ段目の最小の数はｎを用いてイ（3点）（正答率74.4%（無答率6.7%))と表される。

（2）ｍ段目の最小の数と、ｎ段目の２番目に大きい数の和が４の倍数となることを、ｍ、ｎを用いて説明しなさい。
  （4点）（4点評価20.0%、4点評価15.3%（無答率40.0%))

（3）ｍ、nを20未満の自然数とする。ｍ段目の最小の数と、ｎ段目の2番目に大きい数がともにＢ列にあるとき、この２数の和が12の倍数となるｍ、ｎの値の組み合わせは何組あるか求めなさい。
（5点）（正答率6.5%（無答率28.3%))

[next_p]