2021年、千葉県公立高校入試「数学」第5問（総合問題・配点15点）問題・解答・解説

【解答】

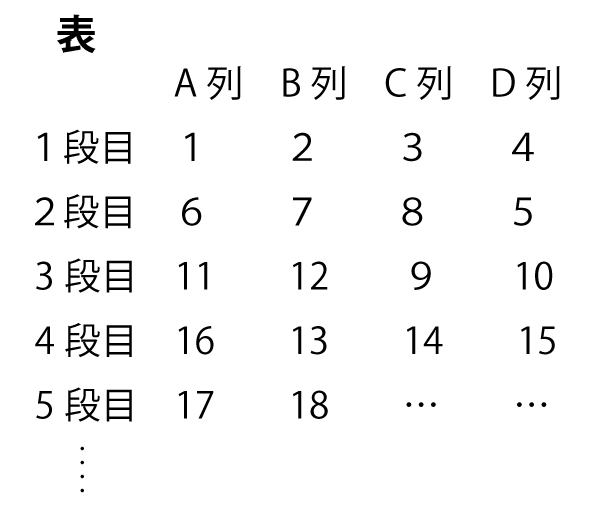
（1）ア 4n （3点）（正答率88.5%（無答率4.0%))
イ 4n－3  （3点）（正答率74.4%（無答率6.7%))

（2）ｍ段の最小の数は4m－３、ｎ段の2番目に大きい数は４ｎー１である。したがってその和は
　　　（4m－３）＋（4ｎ−1）＝４ｍ＋４ｎ−４＝４（ｍ＋ｎ−1）で、４の倍数となる。
（4点）（4点評価20.0%、4点評価15.3%（無答率40.0%))

（３）7組（5点）（正答率6.5%（無答率28.3%))

【解説】

（1）１段に４個の数字があるので、ｎ段までには4n個の数字がある。したがってｎ段目の最大の数は４ｎである。n段目の最小の数は、ｎ段目の最大の数である4ｎから３を引いたと考えて4n-３。
（あるいは、一つ手前の（n-1)段目の最大の数は４（n-1)＝4n-4なので、n段目の最小の数は、その次の数となり4n-4+1=4nー3。）と考えてもよい。
（2）解答の通り。
（3）数の大きさの並びの規則性は、4段ごとの繰り返し配列となるため、4段の数字16個を1群と考えてみる。すると20段未満の数では、１群目、2群目、3群目、4群目、５群目と5群ある。ただし、5群目の最後の段（20段目）は「20未満」に含まれない。下の図のように、各群の最大の数に注目すると16の倍数であり、その群は各数は、その最大の数から１～15を引いた数として表現できる。

ｎ段目がa群目、ｍ段目がｂ群目に含まれるとする。ただし、同じ群に含まれてもいいのでa=bもありうる。そしてaは１群目～5群目までありうるが、ｂ群は5群目は20列目となり「20未満」と矛盾するので１群目～4群目がありうる。つまり「１≦a≦5、１≦ｂ≦4で,a=bも可能」という条件となる。

2数の和は
（16a－９）＋（16a－3）＝16a＋16ｂ－12＝４（4a+4b－３）
（2）と同じ発想で、これは必ず４の倍数である。12の倍数となるためには（4a＋4b−３）が３の倍数であればよい。
4a＋4b−３＝4(a+b)－3なので、a+bが３の倍数ならば、３の倍数となる。

「１≦a≦5、１≦ｂ≦4で,a=bも可能」で、a+bが３の倍数となる場合を考えてみる。
a=1、b=2  （a+b=３）
a=2、b=1　（a+b=３）
a=2,b=4   （a+b=6）
a=3,b=3  （a+b=6）
a=4,b=2   （a+b=6）
a=5,b=1   （a+b=6）
a=5,b=4  （a+b=9）

７通り

ｎ、ｍに直してみると
ｎ＝2,ｍ＝８
n=6、m=4
n=6 、m=16
n=10、m=12
n=14、m=8
n=18、m=4
n=18,m=16
（出題では、m,nの順に問われているが、本説明では、ｎ、ｍの順とした。その理由は、上記図で、ｍは20列目は除外というイメージのため、ｍのほうを後に持ってきた説明の流れの都合上であり、それ以上の意味はない。）

★過去の第5問（総合問題）出題

2020年前期、第5問（総合問題）（玉の数を増やす箱）（計15点）
2019年前期、第5問（総合問題、円錐・円柱・球の体積）（計15点）
2018年前期、第5問（総合問題、並べた紙の枚数）（計15点）
2018年前期、第5問（総合問題、並べた紙の枚数）解説動画（計15点）
2017年前期、第5問（総合問題、タイルを並べた枚数）（計15点）
2017年前期、第5問（総合問題、タイルを並べた枚数）動画解説（計15点）
2016年前期、第5問（総合問題・ランプ点灯パターン）（計15点）
2015年前期、第5問（数の規則性・格子点）（計15点）
2014年前期、第5問（総合問題）（計15点）