2016年前期、千葉県公立高校入試「数学」第5問（総合問題・ランプ点灯パターン）解答・解説

2016年２月９日（火）に実施された2016年前期、千葉県公立高校入試「数学」第5問（総合問題・ランプ点灯周期）問題・解答・解説です。試験問題は白黒ですが、画面上ですので一部カラーを使いました。また、各小問の配点千葉県教育委員会発表の正答率（無答率）も併記しました。

第5問第5問（総合問題・ランプ点灯パターン）（計15点）

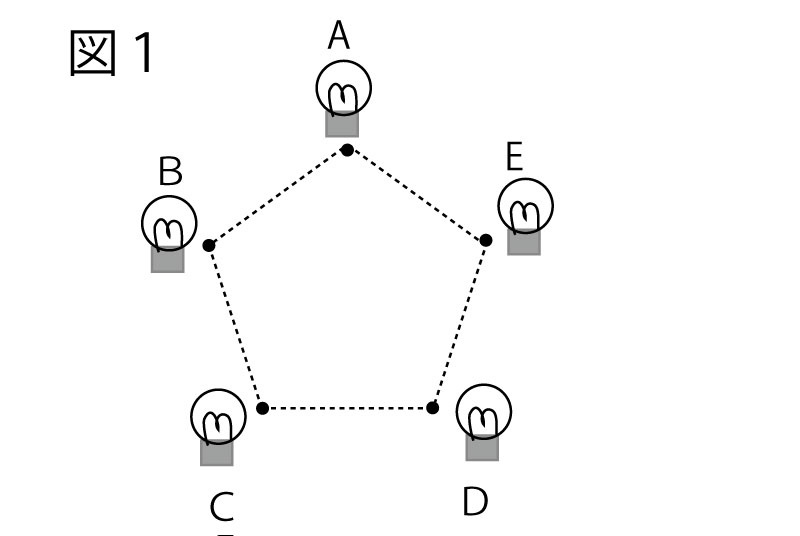
図１のように正五角形の頂点の位置（●）に、A～Eの電球が置いてあり、１つのボタンの操作により、それぞれが「点灯している状態」か「点灯していない状態」になる。

A～Eの電球は、操作を始める前、すべて「点灯している状態」にあり、操作を始めてからは、次の規則にしたがう。

規則
Aの電球：ボタンの操作2回ごとに「点灯している状態」になる。
Bの電球：ボタンの操作3回ごとに「点灯している状態」になる。
Cの電球：ボタンの操作4回ごとに「点灯している状態」になる。
Dの電球：ボタンの操作5回ごとに「点灯している状態」になる。
Eの電球：ボタンの操作6回ごとに「点灯している状態」になる。

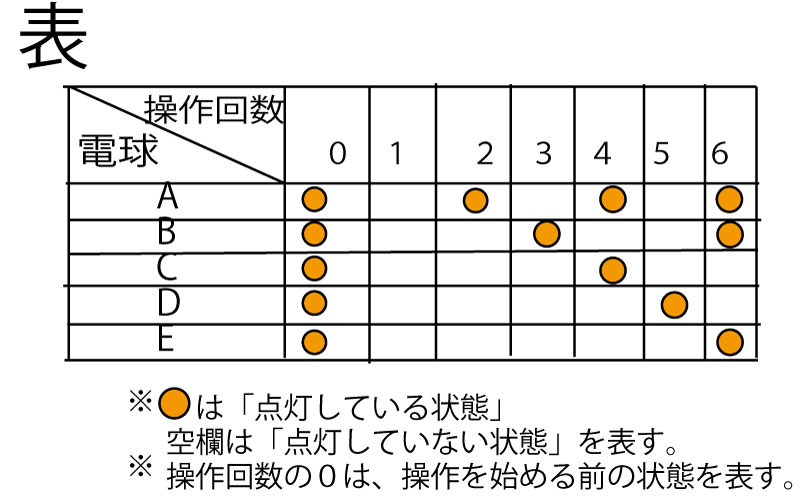
例えば、Aの電球は、「点灯している状態」からボタンを1回操作すると「点灯していない状態」になり、続けてボタンを1回操作すると「点灯している状態」になる。　表は、ボタンの操作が6回までの電球の状態を表したものである。
このとき、あとの（1）～（3）の問いに答えなさい。

（1）ボタンの操作回数が10回のとき、「点灯している状態」の電球をすべて　選び、A～Eの符号で答えなさい。（3点）
　　　　　                                                                                               （正答率89.0%（無答率2.3%))

（2）次の説明は、A～Eの電球の状態について述べたものである。 a（4点）（正答率57.5%（無答率10.6%))、
         b（4点）（正答率13.0%（無答率15.7%))　に入る数をそれぞれ書きなさい。

説明
操作をはじめてから、次にA～Eすべての電球が「点灯している状態」になるのは、ボタンの操作回数がa回のときである。また、a回までの間に、すべての電球が「点灯していない状態」になるのは。全部でb回ある。

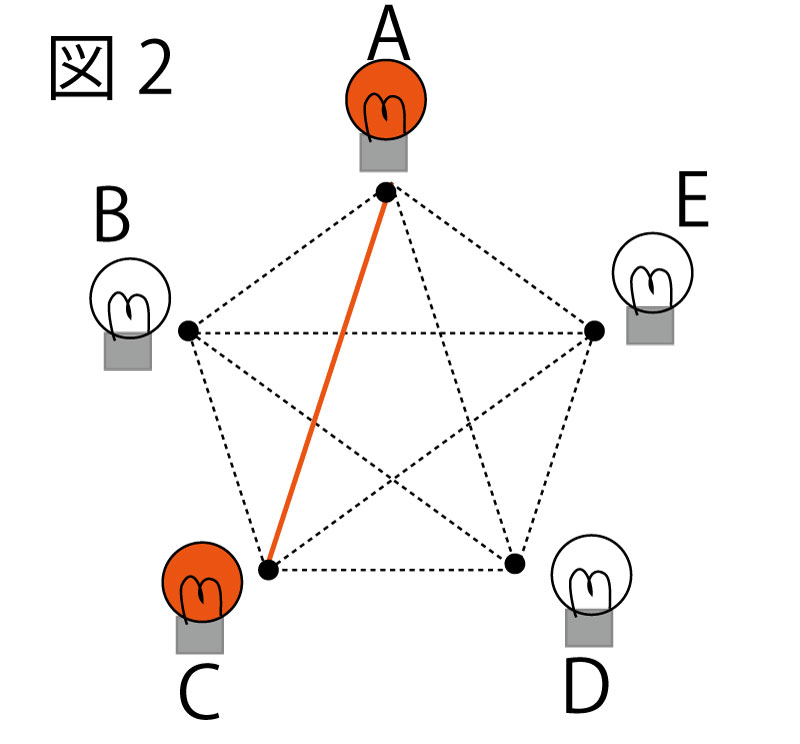
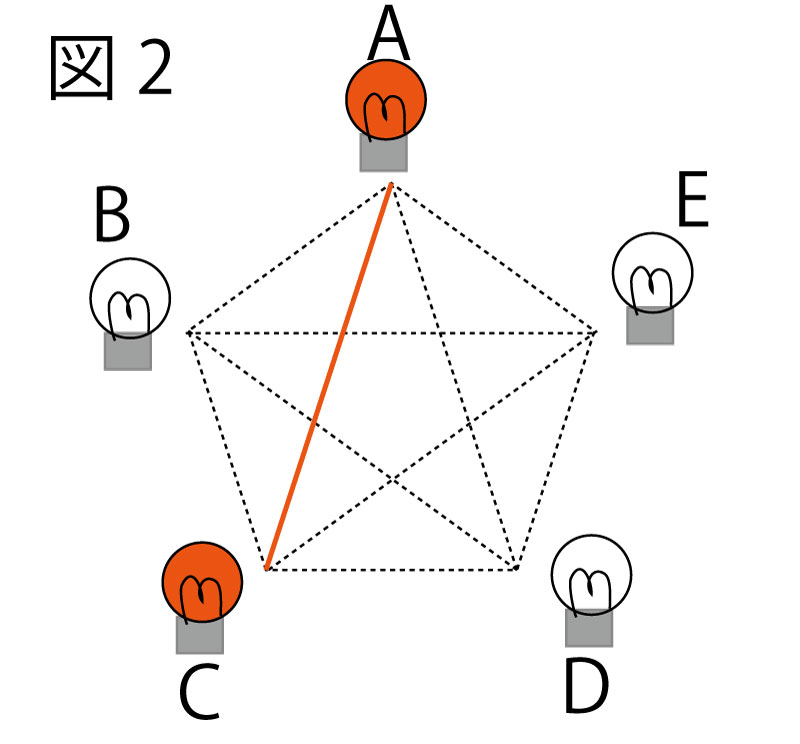
(３）ボタンの操作により、「点灯している状態」になった電球の位置にある点を　それぞれ結ぶ。例えば、図２の太線は、ボタンの操作回数が4回のときのものである。ボタンの操作回数が205回までの間に、A～Eの電球のうち、「点灯している状態」の電球が３つで、その電球の位置にある点を結んでできる図形が、正五角形の　１つの辺と２つの対角線からなる三角形になるのは何回あるか、求めなさい。（4点）（正答率3.0%（無答率42.4%))