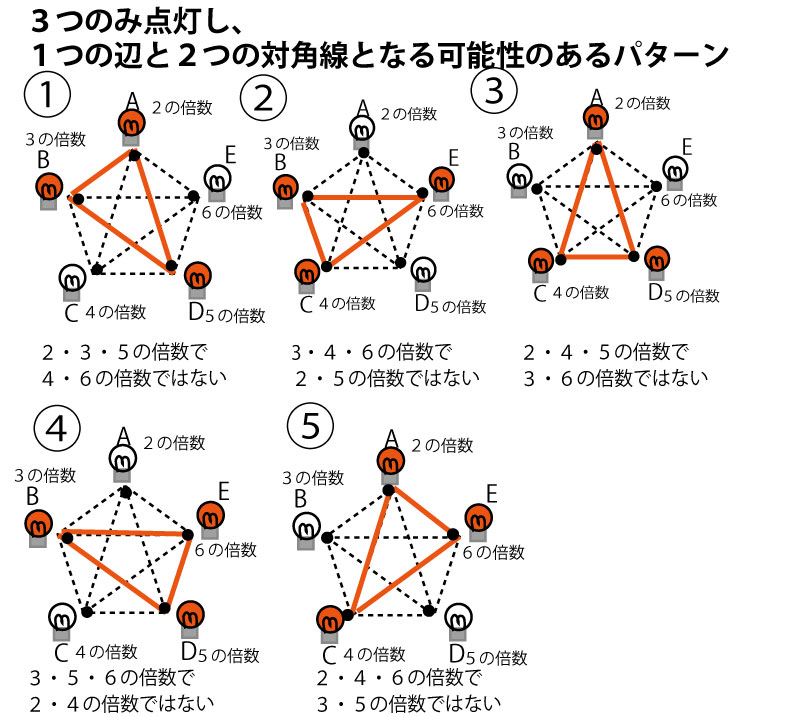
2016年前期、千葉県公立高校入試「数学」第5問（総合問題・ランプ点灯パターン）解答・解説

第5問第5問（総合問題・ランプ点灯周期）解答（計15点）

（1）A、D（3点）  （正答率89.0%（無答率2.3%))
（2）a 60（4点）（正答率57.5%（無答率10.6%))
       b 16（4点）（正答率13.0%（無答率15.7%))　
（3）7回（4点）（正答率3.0%（無答率42.4%))

解説
Aは２の倍数（偶数）、Bは３の倍数、Cは４の倍数、Dは５の倍数、Eは６の倍数ごとに点灯する。
（1）10回は、２の倍数なのでAが点灯、また同時に、５の倍数なのでDが点灯する。
（2）２と３と４と５と６の最小公倍数の時、はじめてすべての電球が点灯する。
一番周期が大きい５と6の最小公倍数は30、これは２・5の倍数ではあるが、4の倍数ではない。
したがって30と4の最小公倍数であるa60回(aは60）で最初に全電球が点灯する。
すべての電球が点灯しないのは、２・３・４・５・６の倍数いずれでもない回数。60までの数字を表にして考えてみる。

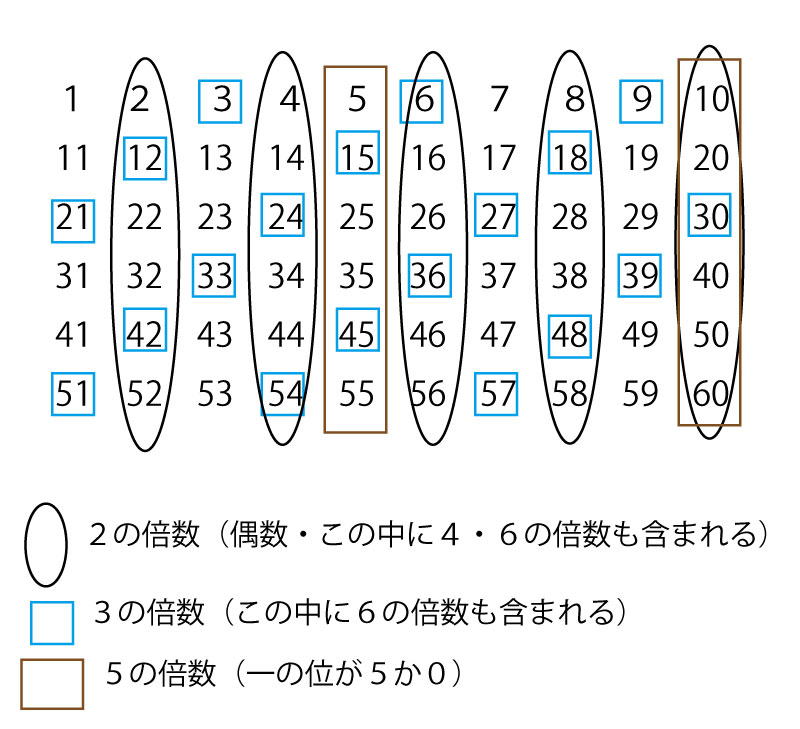
するとどの倍数でもないものは表の中で何にも囲まれていない部分で、
１・７・11・13・17・19・23・29・31・37・41・43・47・49・53・59の16回。（ｂは16）
（3）

それぞれのパターンが本当にありうるのか検証してみよう。簡略化のため図はなくして、数の倍数関係だけを考えてみよう。

更に検証を進めると以下のようになる。