2016年前期、千葉県公立高校入試「数学」第4問(図形の証明)解答・解説
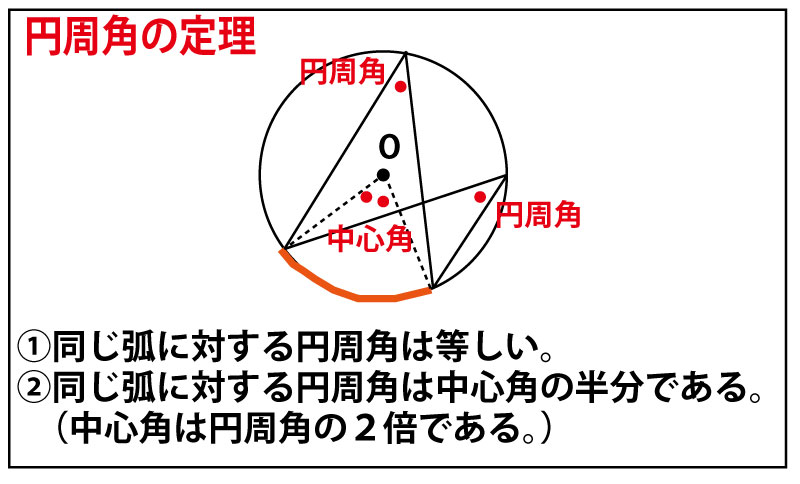
2016年前期、千葉県公立高校入試「数学」第4問(図形の証明)問題・解答・解説です。入試問題は白黒ですが、画面上ですので一部説明などにカラーを使いました。
第4問(図形の証明)(計15点)
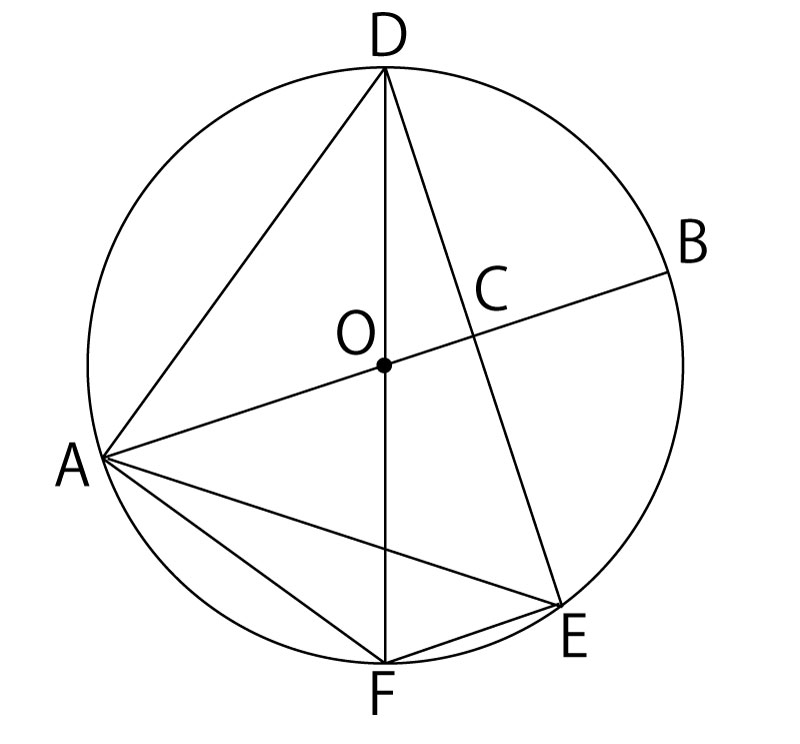
図のように、線分ABを直径とする円Oがある。線分OB上に、2点O、Bと異なる点Cをとる。点Cを通り、線分OBと垂直に交わる直線と、円との交点をD、Eとする。また線分DOの延長線と円との交点をFとする。3点A、E、Fをそれぞれ結び、2点A、Dを結ぶ。このとき、次の(1)(2)の問いに答えなさい。
(1)△AOF∽△DAEとなることの証明を![]() の中に途中まで示してある。a(2点),b(2点)に入る最も適当なものを、選択肢のア~カのうちからそれぞれ1つずつ選び、符号で答えなさい。また、c(6点)には証明の続きを書き、証明を完成させなさい。ただし、
の中に途中まで示してある。a(2点),b(2点)に入る最も適当なものを、選択肢のア~カのうちからそれぞれ1つずつ選び、符号で答えなさい。また、c(6点)には証明の続きを書き、証明を完成させなさい。ただし、![]() の中の
の中の![]() に示されている関係を使う場合、番号の
に示されている関係を使う場合、番号の![]() を用いてもかまわないものとする。
を用いてもかまわないものとする。
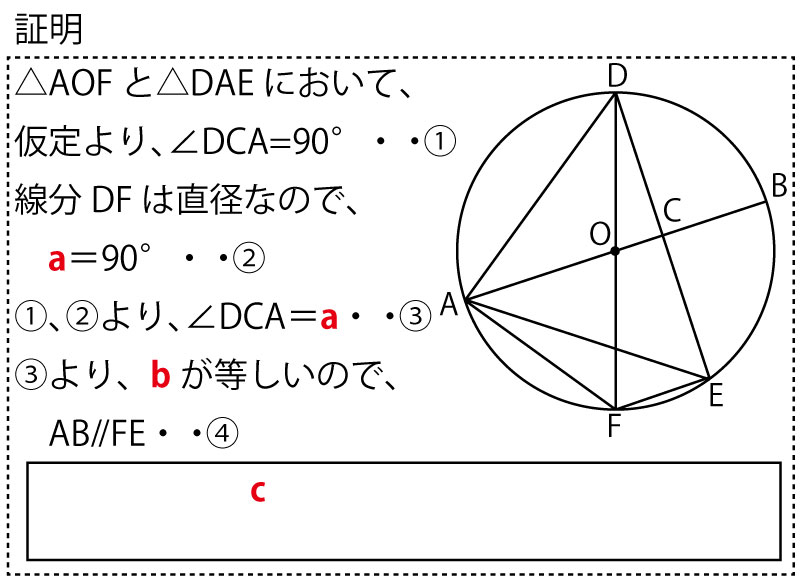
選択肢 ア∠EAD イ∠DEF ウ∠FDA エ円周角 オ対頂角 カ同位角
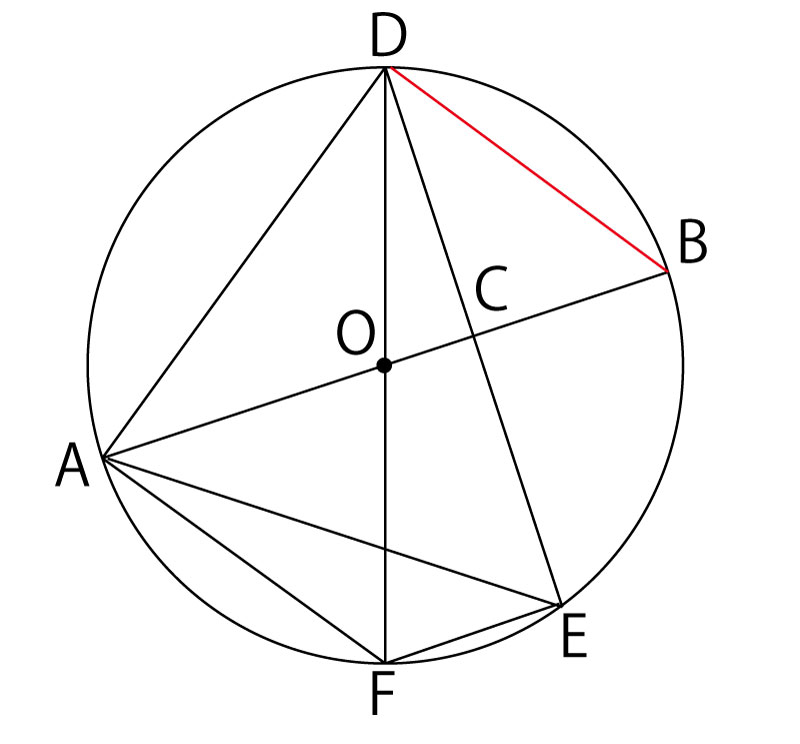
(2)2点B、Dを結ぶ。円Oの半径は5cm、BD=6cm のとき、△AEFの面積を求めなさい。(5点)
[next_p]