2016年前期、千葉県公立高校入試「数学」第4問（図形の証明）解答・解説

2019年7月29日 2019年7月29日

asakura

【第4問】（図形の証明）（計15点）解答例

解説

千葉県公立高校入試「図形の証明」の問題は、人口が多い7都府県（東京都、神奈川県、埼玉県、千葉県、大阪府、兵庫県、愛知県）の公立高校入試の中で最も難しい。例年、15点配点で、（1）の証明の（a)（2点）(b)（2点）を選択肢から選ばせ、（c）で証明の後半を記述させ（6点）、最後に（2）で（1）の証明結果を使った計算を問う（5点）。
正答率は選択肢を記号で選ばせる(1)(a)(b)では毎年高いが、（c）（証明記述）と（2）（証明結果をもとにした計算）は毎年、正答率は低い
したがって、受験生としては、（1）（c）と（2）（計11点）はあきらめ、（a)(b)（計4点）だけを正確に答え、考える時間・検算する時間を他の問題に振り向けたほうがよい。
とはいっても、（a)(b)を確実に正解にするためにも、また可能ならば（c)や（2）を最初からあきらめるのでなく、他の問題を解いた上で、残った時間で、最後に（c)や（2）に戻り、得点できればまでできれば、うれしい。そこで以下のように、千葉県独特の問題の構成と発想をあらかじめ理解しておけば、（c）（2）も解くことができる（ｃで6点でなくても部分点3点を得ることができる）可能性があるので、しっかり理解しておこう。

このように証明の前半（この中に（a)(b)もあり）で手段を示し、その結果を使い、本文の冒頭に書いてある目的を証明させるという構成になっている。
（c）部分を解くためには目的にいたる方法を予測することは重要である。
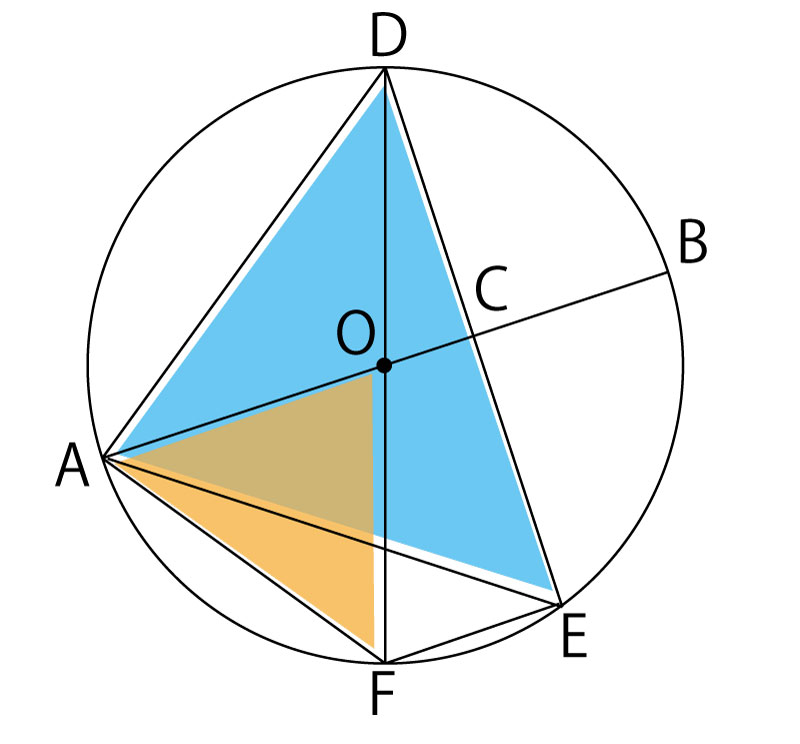
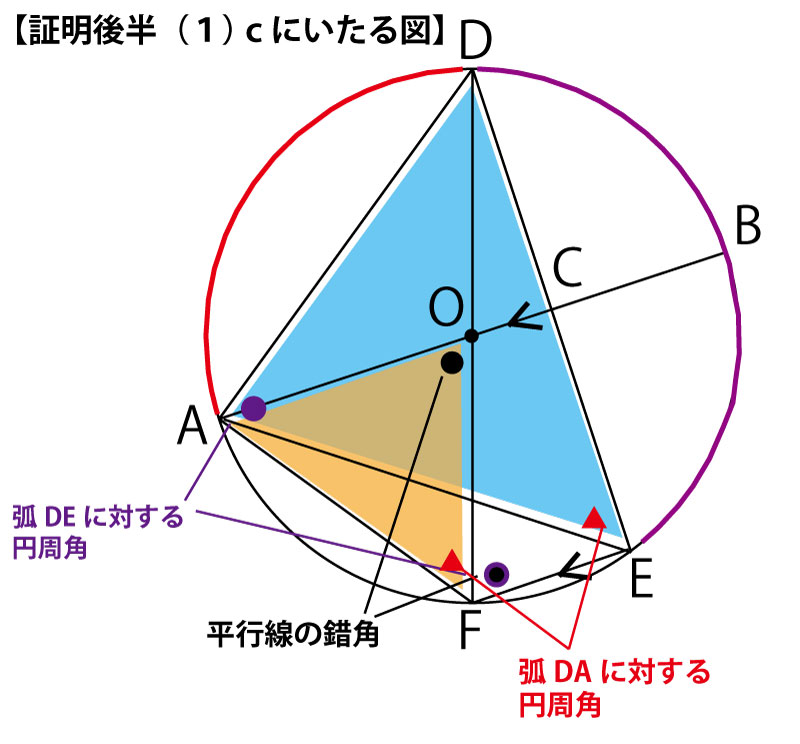
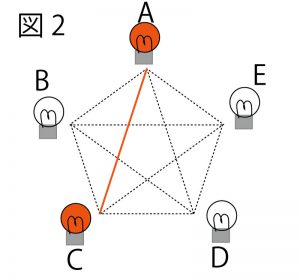
この証明の目的は△RQE∽△SGFという三角形の相似の証明である。まず、その三角形を図の中で確認してみよう。

少し重なりがあるが、図の青い三角形とオレンジの三角形である。

次の３つの「三角形の相似条件」のうちどれを使って証明していくのかを予測してみよう。

三角形の相似条件は教科書では、出る順番が逆で、
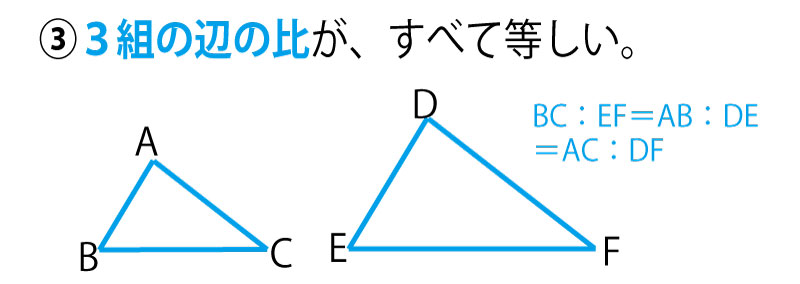
「3組の辺の比が、すべて等しい」
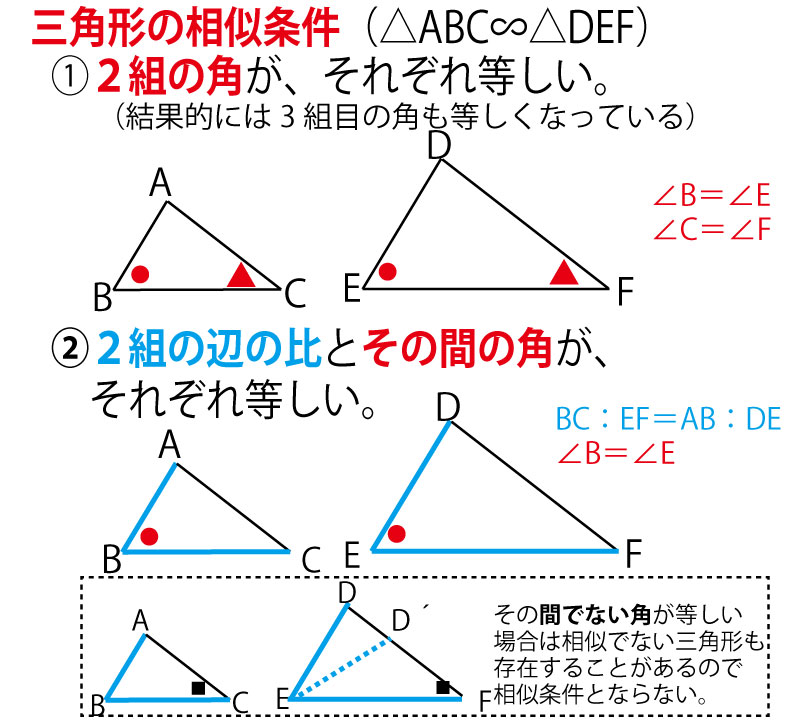
「2組の辺の比とその間の角が、それぞれ等しい」
「2組の角が、それぞれ等しい」
の順に書かれていることが多い。
ただ、多くの「図形の証明」の入試問題は、辺比を数値で示すよりも、図形から、対頂角、平行線の錯角・同位角などを活用しながら「角が等しい」ことを見ぬかせて解かせる問題となっている。したがって、入試的には上記の番号順に使われると考えておいたほうがよい。

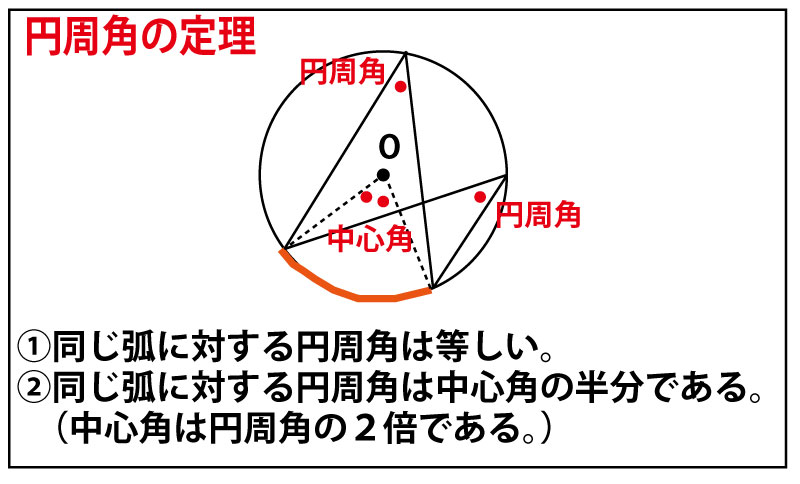
また本設問では、三角形の相似関係を証明させるのに、上記のように角度が重視されていることが推測される。加えて、図に円が描かれている。図に円が描かれている場合、円周角の定理を証明などに使っていることが多い。円周角の定理（関連してタレスの定理）をまとめておこう。

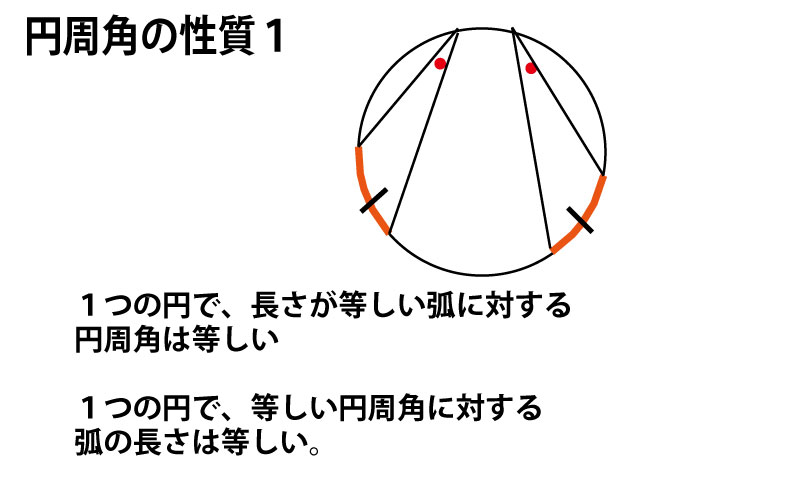
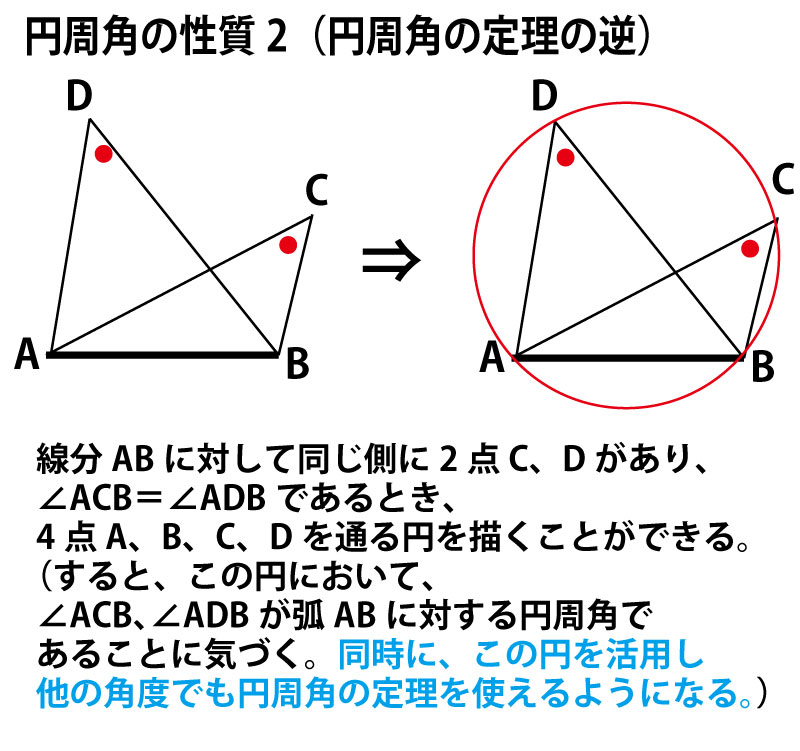
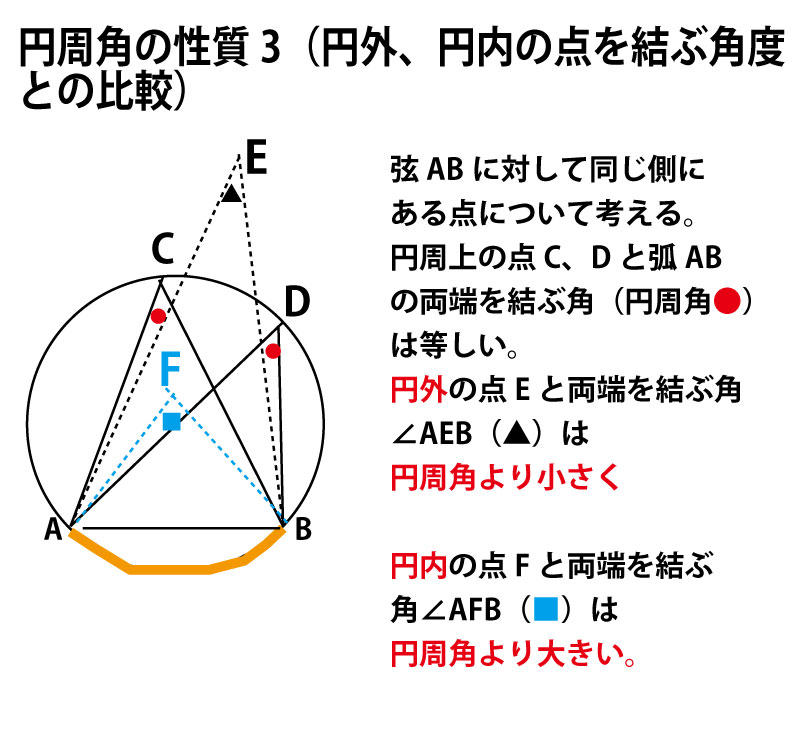
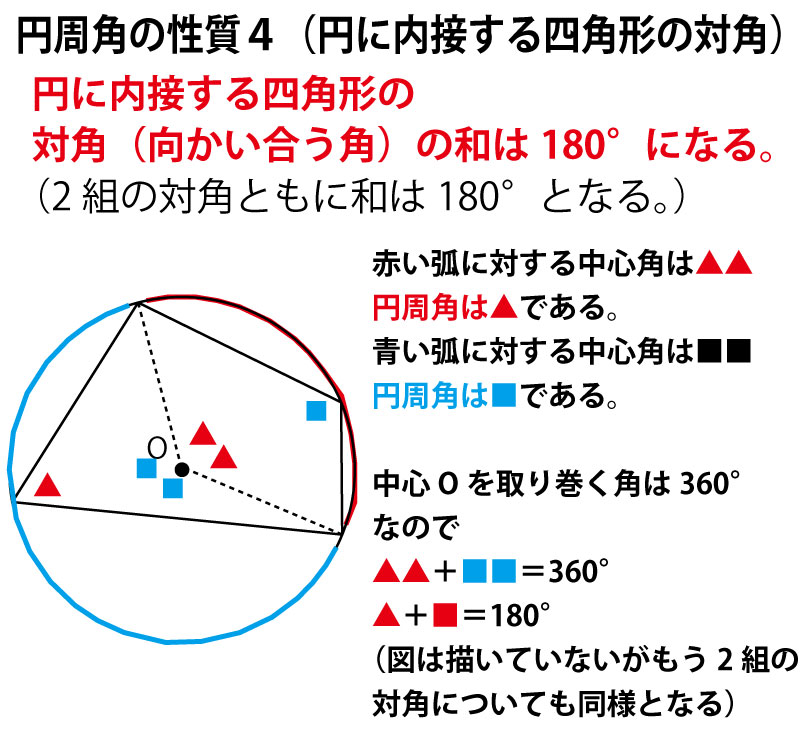
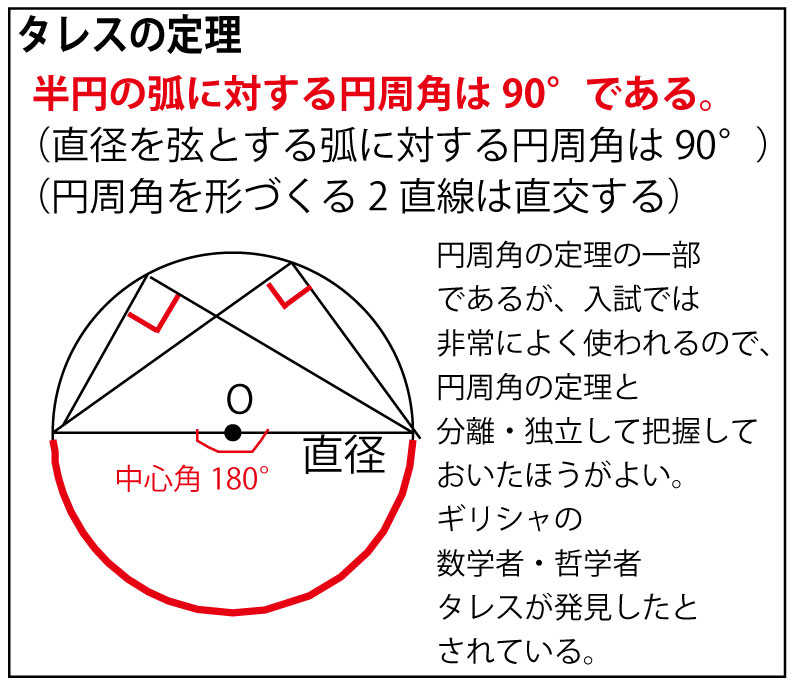
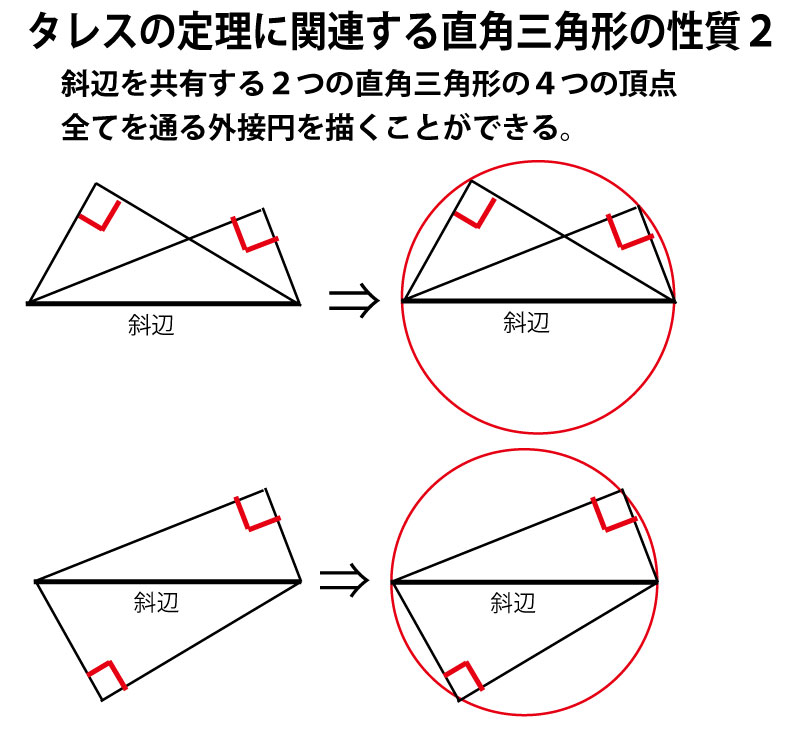
円周角の定理（タレスの定理）のまとめ

（上記のように円周角の定理・タレスの定理では、問題文に最初に円が描かれていない場合でも、あとから円を描くことができる。そして、最初に描かれていない円を描くことで、別の部分の角度に円周角の定理やタレスの定理を活用することができ、「ドミノ倒し的」に証明のヒントが見つかっていく場合もある。）

第１問(1)（a)(b)証明の前半の解説

図が３つあるうちの一番上の図に、この証明の前半の流れを描きこんでいく。

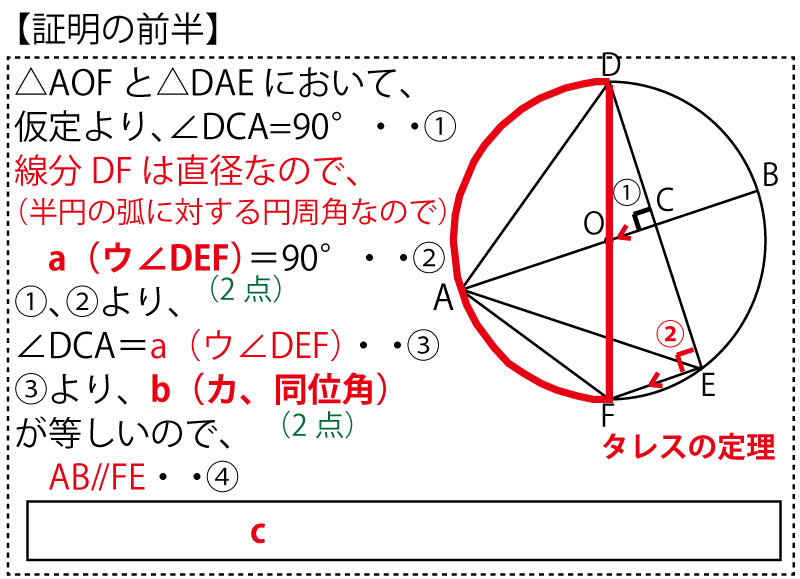
次に２番目の図には、照明前半で求めたAB∥FEを示す矢羽根と、相似を証明すべき三角形に注目し（斜線で軽く強調するなどし）、相似を証明できそうな2組の角を発見していく。

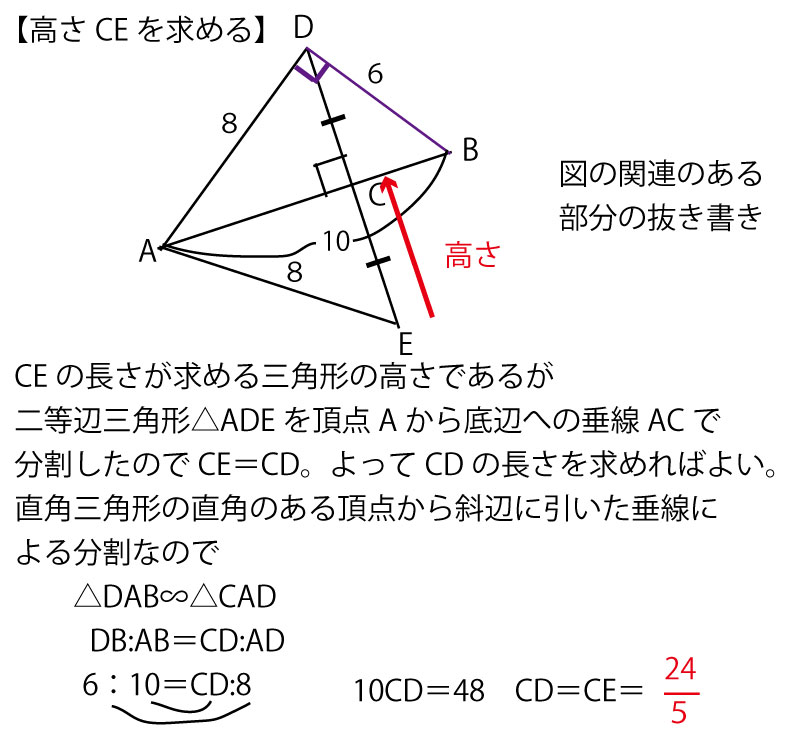
（2）解説

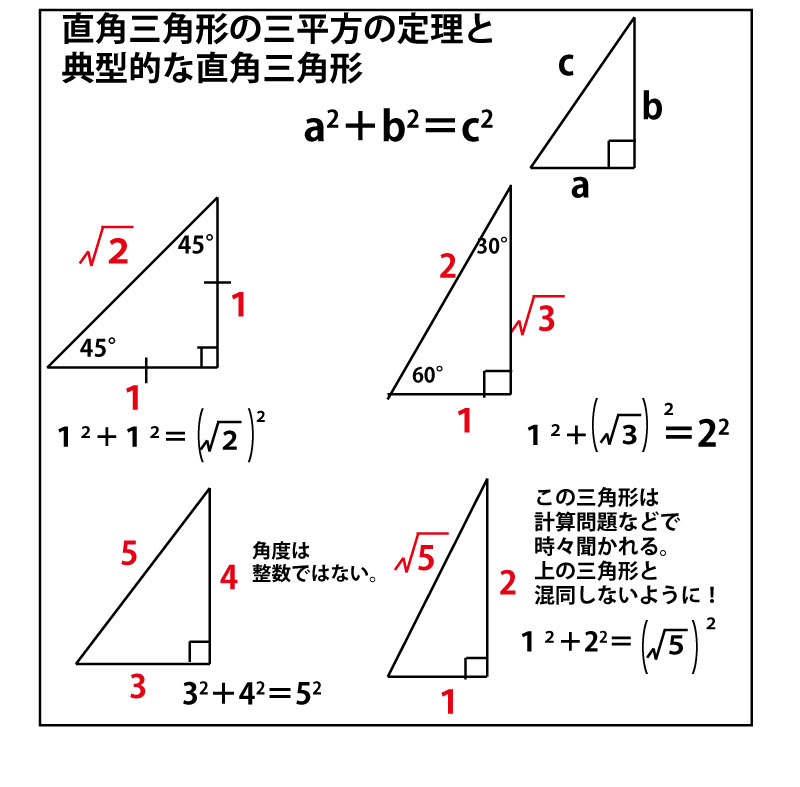
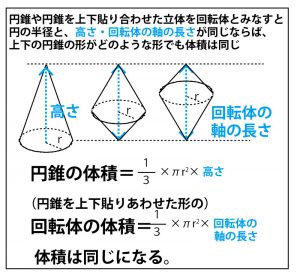
長さの計算の際には典型的な直角三角形の辺の比が聞かれることが多いので整理しておこう。

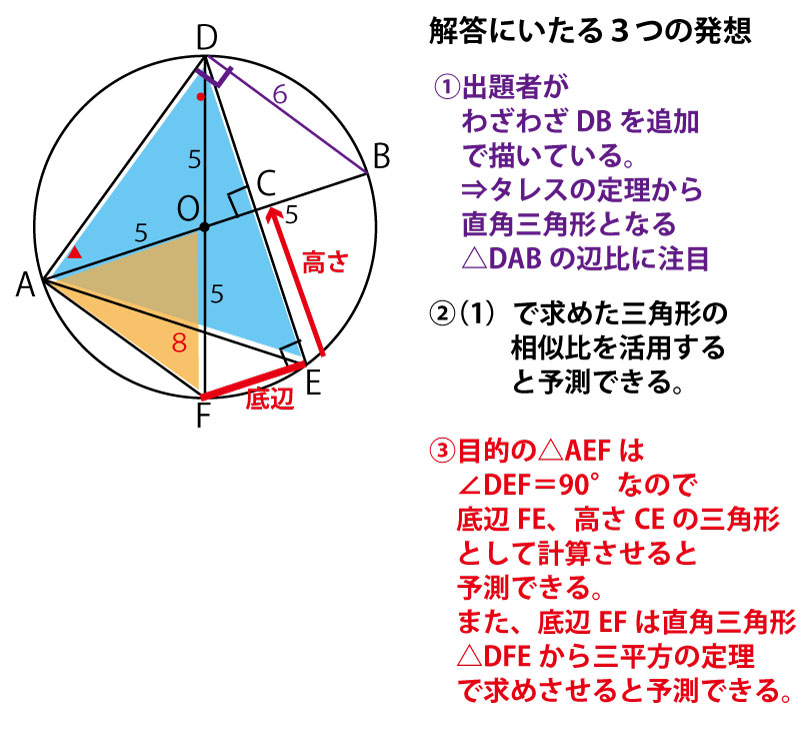
【注目点のまとめ】
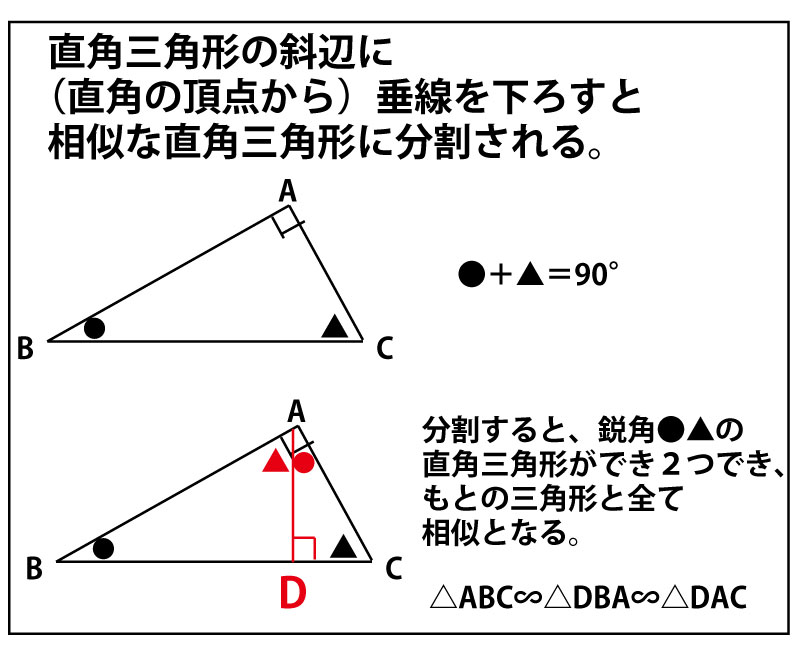
・△DABはタレスの定理から直角三角形とわかり、斜辺AB（直径）＝10、DB＝６なので、典型的な辺比３：４：５の直角三角形なので
DA＝８
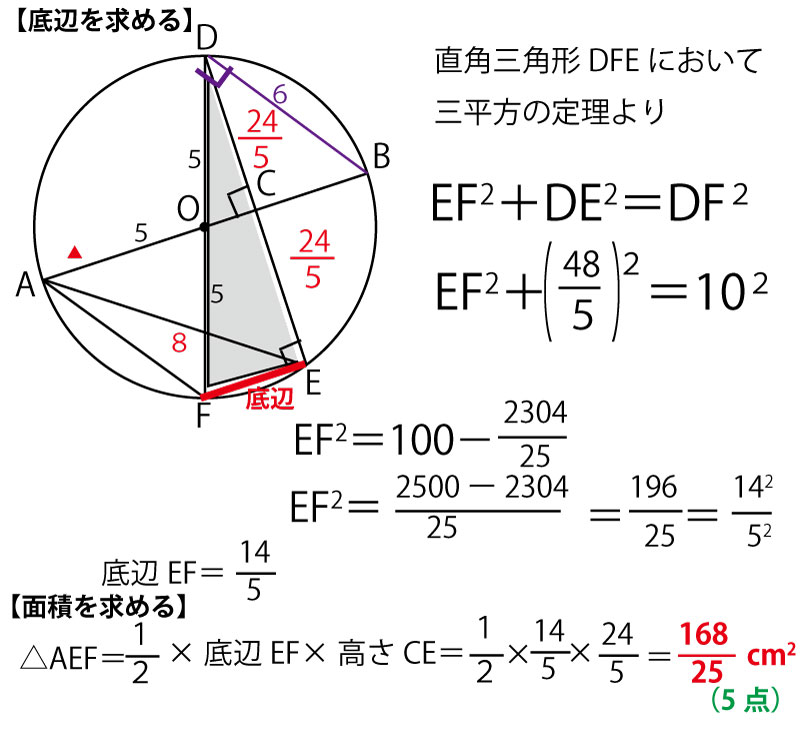
・前問で求めた△AOF∽△DAEで、AO＝OF＝５（半径）。上記よりAD（＝AE）＝８なので、△AOFと△DAEの相似比は５：８
それでは解いていこう。