3次関数f(x)はx=-1で極小値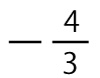 をとり、x=3で極大値をとる。また、曲線y=f(x)は点(0,2)を通る。
をとり、x=3で極大値をとる。また、曲線y=f(x)は点(0,2)を通る。
(1)f(x)の導関数f´(x)はカ次関数であり(カ、1点)、f´(x)は
(x+キ)(x-ク)(キク、あわせて2点)
で割り切れる。
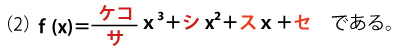 (あわせて3点)
(あわせて3点)
(3) 方程式f(x)=0は、三つの実数解をもち、そのうち負の解はソ個(2点)である。
また、f(x)=0の解をa、b、c(a<b<c)とし、曲線y=f(x)のa≦x≦bの部分と、x軸とで囲まれた図形の面積をS、曲線y=f(x)のb≦x≦cの部分とx軸とで囲まれた図形の面積をTとする。
このとき

(タ 3点)
[next_p]