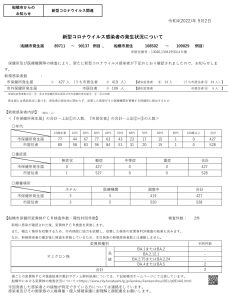
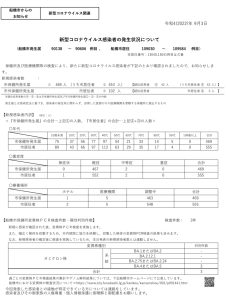
2018年大学入試センター試験「数学ⅡB」第2問(計30点)問題・解答・解説
2022年9月 予備校講師・船橋市議 朝倉幹晴
2018年大学入試センター試験「数学ⅡB」第2問(計30点)の問題・解答・解説を作りましたので、学習や入試対策にご活用ください。
2018年大学入試センター試験「数学ⅡB」第2問(計30点)
p>0とする。座標平面上の放物線y=px2+qx+rをCとし、直線y=2x-1をℓとする。Cは点A(1,1)においてℓと接しているとする。
(1)qとrを、pを用いて表そう。放物線C上の点Aにおける接線の傾きはア(1点)であることから、q=イウp+エ(あわせて2点)がわかる。さらに、Cは点Aを通ることから、r=p-オ(2点)となる。
(2)v>1とする。放物線Cと直線ℓおよび直線x=vで囲まれた図形の面積Sは
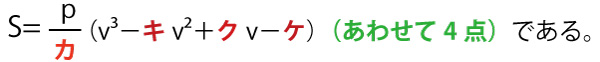
である。また、x軸とℓおよび2直線x=1、x=vで囲まれた図形の面積TはT=vコ-v(2点)である。
U=S-Tはv=2で極値をとるとする。このとき、p=サ(3点)であり、v>1の範囲でU=0となるvの値をvoとすると、

1<v<voの範囲でUはソ(2点)。ソに当てはまるものを、次の![]() のうちから一つ選べ。
のうちから一つ選べ。
P=サのとき、v>1におけるUの最小値はタチ(3点)である。
[2]関数f(x)はx≧1の範囲でつねにf(x)≦0を満たすとする。t>1のとき、曲線y=f(x)とx軸および2直線x=1、x=tで囲まれた図形の面積をWとする。tがt>1のとき、曲線y=f(x)とx軸および2直線x=1、x=tで囲まれた図形の面積をWとする。tがt>1の範囲を動くとき、Wは、底辺の長さが2t2ー2、他の2辺の長さがそれぞれt2+1の二等辺三角形の面積とつねに等しいとする。このとき、x>1におけるf(x)を求めよう。
F(x)をf(x)の不定積分とする。一般に、F(x)=ツ(1点)、W=テ(3点)が成り立つ。ツ、チに当てはまるものを、次ののうちから一つずつ選べ。ただし、同じものを選んでもよい。
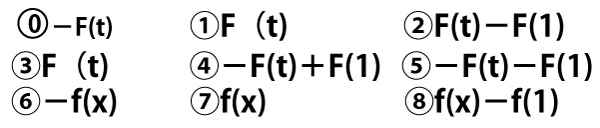
したがって、t>1において
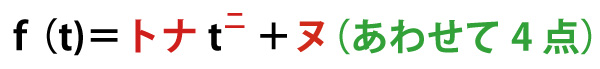
である。よって、x>1におけるf(x)がわかる。