2012年前期、千葉県公立高校入試「数学」第2問（2）（角度を求める問題、配点5点）問題・解答・解説
asakura
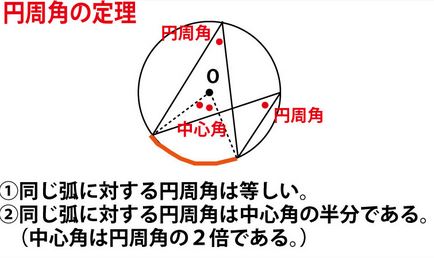
【解答】66°（5点）（正答率43.9%（無答率13.8%))
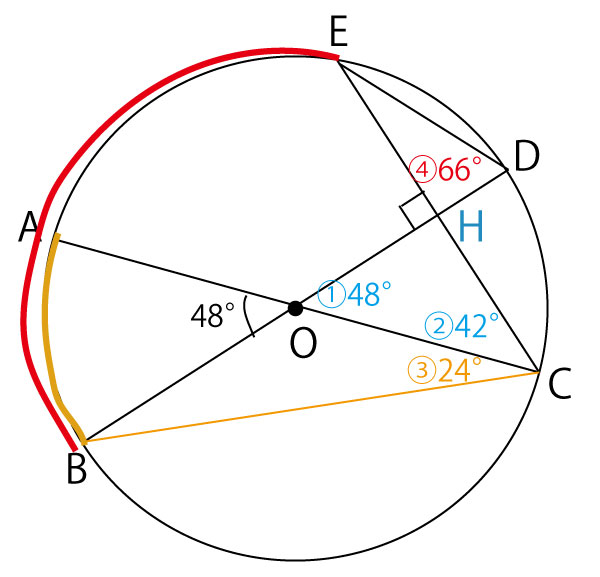
考え方
∠AOBの対頂角で∠DOCは48°
BDとCEの交点をHと置く。∠OHC＝90°で△OHCは直角三角形であり、直角以外の２つの鋭角の和は90°となる。
∠HCO＋∠HOC＝90°。 ∠HCO＝90°−∠HOC＝90°ー48°＝42°
弧ABに対する中心角である∠AOB＝48°である。円周角は中心角の半分となるので。
円周角∠BCA＝１／２ ×48° ＝24°
弧BEに対する円周角は等しいので
∠BDE（●）＝∠BCE。
∠BCE＝∠BCA＋∠HCO（∠ECA）＝24°＋42°＝66°
∠BCE＝66°
