2021年大学入試共通テスト(第1日程)「数学ⅡB」第4問「数列」問題(20点配点)・解答・解説

2022年5月27日 予備校講師・船橋市議(無党派) 朝倉幹晴
2021年共通テスト第2日程の数学ⅡBの解答・解説を作成しました。学習や入試対策にご活用ください。
2021年共通テスト第2日程、数学ⅡB第4問(計20点)
初項3、交差pの等差数列を{an}とし、初項3、公比rの等比数列を{bn}とする。
ただし、p≠0かつr≠0とする。さらに、これらの数列が次を満たすとする。
anbn+1-2an+1bn+3bn+1=0 (n=1,2,3,…)…![]()
(1)pとrの値を求めよう。自然数nについて、an、an+1、bnはそれぞれ
an=ア+(n-1)p …![]() (ア1点)
(ア1点)
an+1=ア+np…![]()
bn=イrn-1(イ1点)
と表される。r≠0により、すべての自然数nについて、bn≠0となる。
![]()
であることから、![]() の両辺をbnで割ることにより
の両辺をbnで割ることにより
ウan+1=r(an+エ)…![]() (ウエ合わせて2点)
(ウエ合わせて2点)
が成り立つことがわかる。![]() に
に![]() と
と![]() を代入すると
を代入すると
(r-オ)pn=r(p-カ)+キ…![]() (オカキ合わせて2点)
(オカキ合わせて2点)
となる。
![]() がすべてのnで成り立つことおよびp≠0により、r=オを得る。さらに、このことから、p=ク(3点)を得る。
がすべてのnで成り立つことおよびp≠0により、r=オを得る。さらに、このことから、p=ク(3点)を得る。
以上から、すべての自然数nについて、anとbnが正であることもわかる。
(2)p=ク、r=オであることから、{an},{bn}の初項から第n項までの和は、それぞれ次の式で与えられる。

(3)数列{an}に対して、初項3の数列{cn}が次を満たすとする。
ancn+1-4an+1cn+3cn+1=0(n=1,2,3,・・・)…![]()
anが正であることから、![]() を変形して、
を変形して、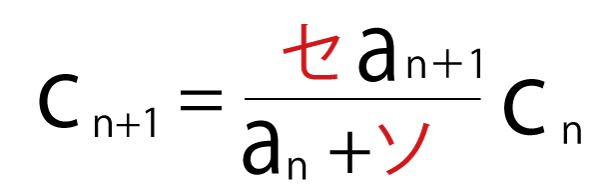 を得る。
を得る。
さらに、p=クであることから、数列{cn}はタことがわかる。
タの解答群
(4)q、uは定数で、q≠0とする。数列{bn}に対して、初項3の数列{dn}が次を満たすとする。
dnbn+1-qdn+1bn+ubn+1=0(n=1,2,3,‥‥)‥‥![]()
r=オであることから、![]() を変形して、
を変形して、
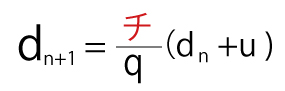
を得る。したがって、数列{dn}が、公比が0より大きく1より小さい等比数列となるための必要十分条件は、
q>ツかつu=テである。
[next_p]