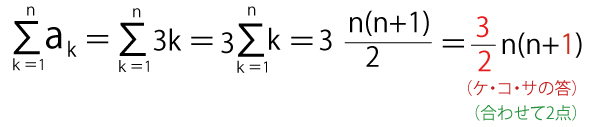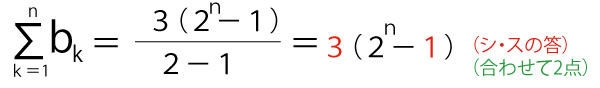2021年大学入試共通テスト（第1日程）「数学ⅡB」第4問「数列」問題（20点配点）・解答・解説

【解説】

初項３、交差ｐの等差数列なので

a_n＝３（ア）＋（n－1）p　（1点）…

a_n+1＝ア＋np…

初項３、公比rの等比数列なので
b_n＝３（イ）r^n－1（1点）

ｒ≠0により、すべての自然数nについて、b_n≠0となる。
a_nb_n+1－2a_n+1b_n＋3b_n+1＝0 (n=1,2,3,…）…

の両辺をb_nで割ると、

にとを代入すると
2a_n＋1＝r(a_n＋3）
2(3+np)＝r{3+(n－1)p＋3}
６＋2np＝r（3+npーp+3)
6+2np=r(np－p+6)
（解答がpnとなっているのでnpをpnに変える）
6+2pn=r(pn－p+6)
2pn－rpn＝－rp+6r－6
両辺に－1をかけて
rpn－2pn＝rp－6r＋6
(r－2)pn＝r(pー6)+6…　(オ、カ、キの答）（合わせて2点）

が全てのｎで成り立つのでnを含む右辺がｎが変化しても変化しない値、つまり０である必要がある。
ｐ≠０より、ｒー２＝０ ｒ＝２（1点）
左辺が０で、ｒ＝２をに代入すると
０＝２（pー6)+6
左辺と右辺を逆にして

２（pー6)+6＝０
2p－12+6＝０
2p－6=0
2p=6  p=3（クの答）（２点）

（2）a_nは、初項３、Ｐ（公差）３なので、a_n＝３＋3（n－1）＝３＋３ｎー３＝3n

bnは初項３、ｒ（公比）２の等比数列なので

（3）数列｛a_n｝に対して、初項３の数列｛c_n｝が次を満たすとする。
a_nc_n+1－4_an+1c_n+3c_n+1＝0（ｎ＝1,2,3,・・・）…

さらに、{a_n}のｐ（交差）＝ク（3）であることから、

（4）q、uは定数で、ｑ≠0とする。数列｛b_n｝に対して、初項3の数列｛d_n｝が次を満たすとする。
d_nb_n+1－qd_n+1b_n+ub_n+1＝0（n=1,2,3,‥‥）‥‥
{bn}no

{b_n}の公比ｒ＝オ（２）であることから、を変形して、

を得る。したがって、数列｛dn｝が、公比が０より大きく１より小さい等比数列となるための必要十分条件は、
q＞ツ（２）（1点）からu＝テ（０）（1点）である。