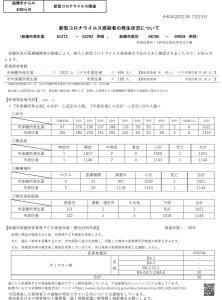
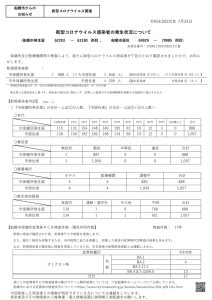
2022年大学入試共通テスト「数学ⅡB」第2問「微分・積分」問題、解答、解説（配点30点）

2022年7月　予備校講師・船橋市議　朝倉幹晴

2022年大学入試共通テスト「数学ⅡB」第2問「微分・積分」の解答、解説（配点30点）を作成しました。学習や入試対策にご活用ください。

2022年共通テスト数学Ⅱb第2問（配点30点）

【1】aを実数とし、f(X)＝x³ー6aｘ+16とおく。
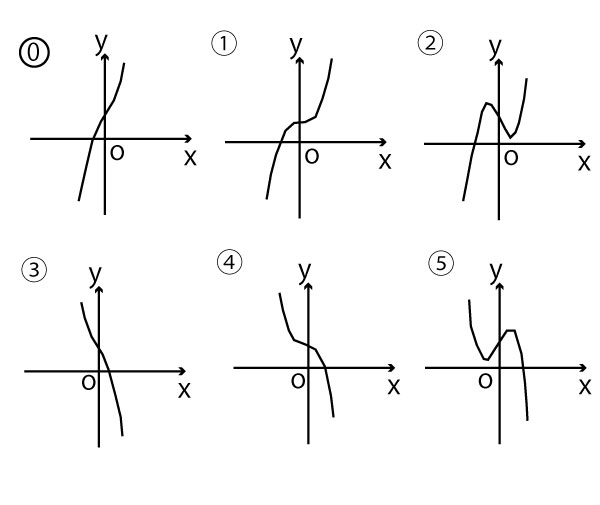
（1）y=f(x)のグラフの概形は
ａ＝0のとき、ア（2点）
a<0のとき、イ（2点）
である。

ア、イについては、最も適当なものを、次ののうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

（2)a>0とし、pを実数とする。座標平面上の曲線y=f(x)と直線ｙ＝ｐが3個の共有点をもつようなｐの値の範囲はウ＜ｐ＜エである。（ウ2点、エ2点）
p＝ウのとき、曲線ｙ＝f(x)と直線y=f(x)と直線y=pは2個の共有点をもつ。それらのｘ座標をq、ｒ（q＜r)とする。曲線ｙ＝f(x)と直線y=pが点（r,p)で接することに注意すると

と表せる。

（3）方程式f(x)=0の異なる実数解の個数をｎとする。次ののうち、正しいものはケとコである。（ケコ、3点×２＝6点）

[2]b>0とし、g(x)＝x³－3bx＋3b²、h(x)=x³－x²＋b²とおく。座標平面上の曲線ｙ＝g(x)をC₁、曲線ｙ＝ｈ（x)をC₂とする。

C₁とC₂は2点で交わる。これらの交点のｘ座標をそれぞれα、β（α＜β）とすると、α＝サ、β＝シスである。（サシス、全部正解であわせて2点）
　α≦ｘ≦βの範囲でC₁とC₂で囲まれた図形の面積をＳとする。また、ｔ＞βとし、β≦x≦tの範囲でC₁とC₂および直線x=tで囲まれた図形の面積をTとする。


[next_p]