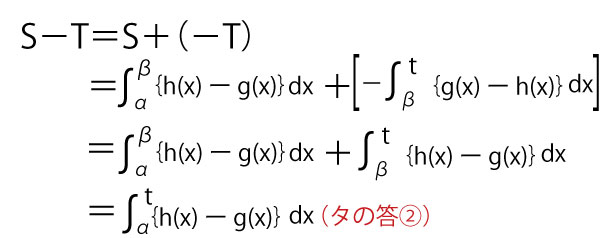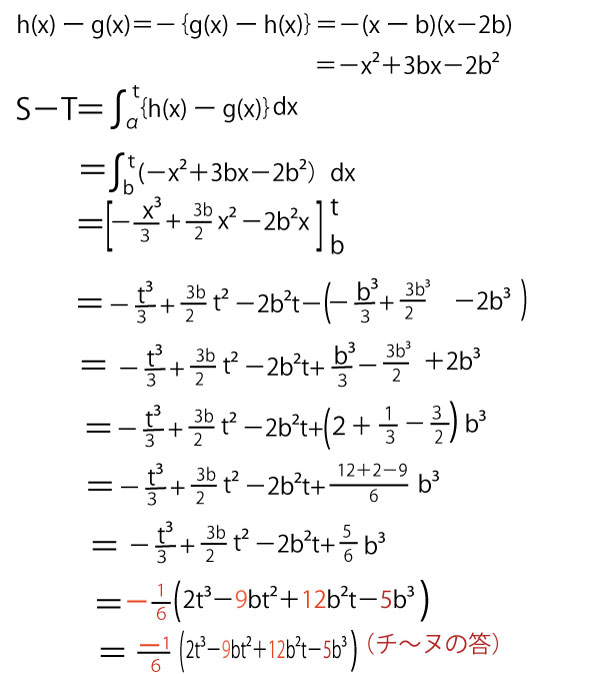2022年大学入試共通テスト「数学ⅡB」第2問「微分・積分」問題、解答、解説（配点30点）

【解説】
f(x)=x³ー6ax＋16
f´(x)＝3x²−6a
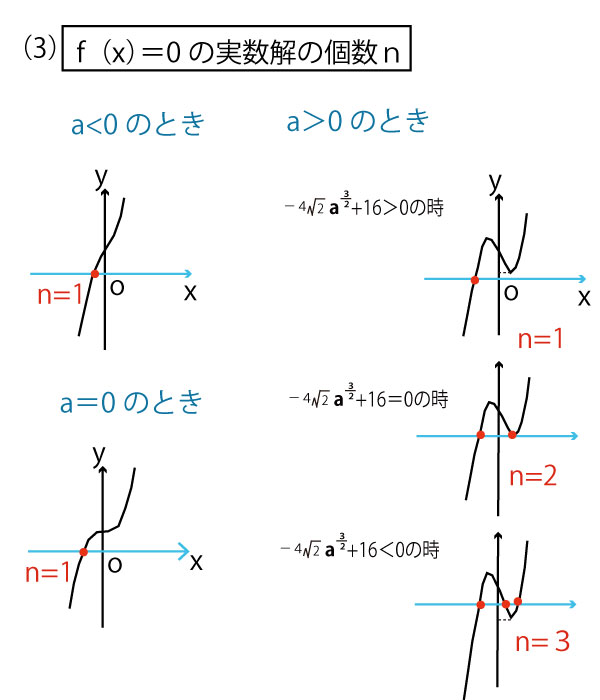
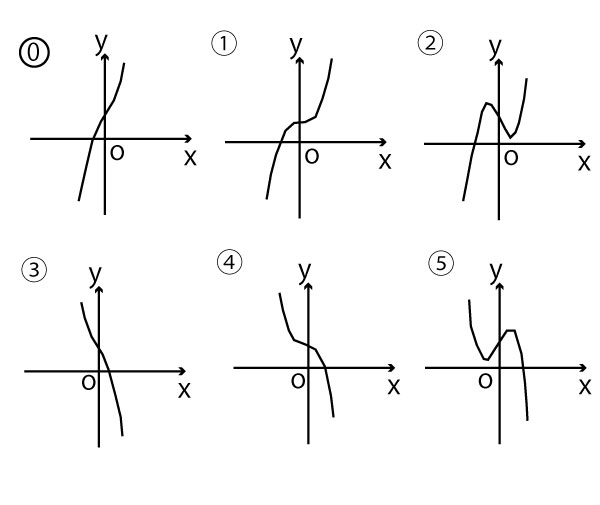
a＝0のとき、
f(x)＝x³＋16　f´（x)=3x²

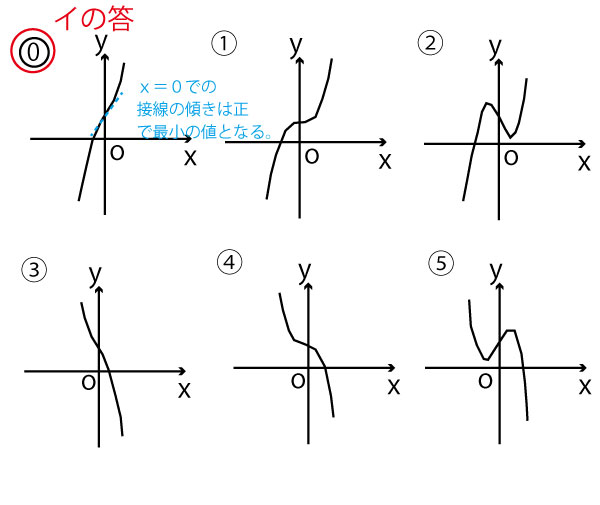
つねに増加し、x=0のときのみ、グラフの接線の傾き0となり、f(0)＝16

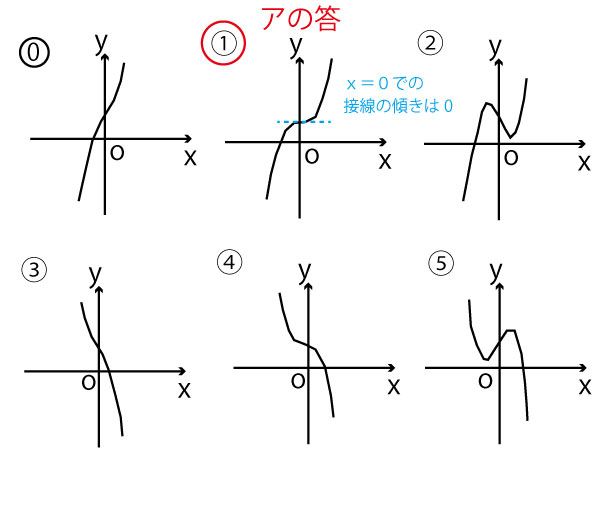
a＜0のとき
f´(x)＝3x²−6a
－6a＞0なのでf´(x)＞0
常に増加する曲線である。ただしx=0のとき、接線の傾きは最小になり、f(o）＝16である。

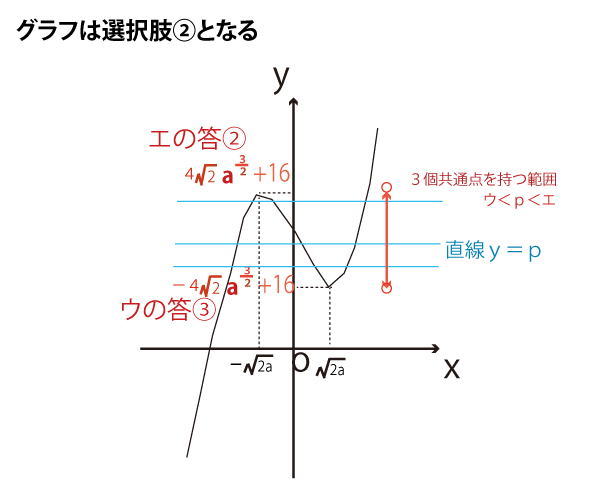
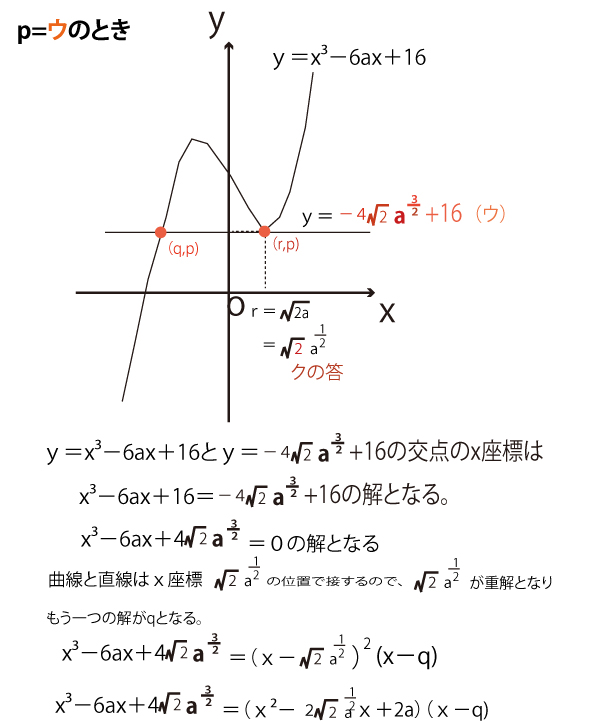
［2］

g(x)とh(x)の交点のｘ座標は、
x³－3bx＋3b²=x³－x²＋b²の解である。
x²ー3bx＋2b²＝0
（x－b)(x－2b)=0
x＝b,2b
b>0なのでｂ＜2b。α＜βなので
α＝b（サの答）、β＝2b（シスの答）
g(x)ーh(x)＝x³－3bx＋3b²−（x³－x²＋b²）

＝x³－3bx＋3b²−x³+x²−b²＝x²−3bx＋2b²
                =（x－b)(x－2b)
b<x<2bの範囲で（x－b)は負の値、(x－2b)は正の値なので
（x－b)(x－2b)＜0
よってg(x)ーh(x)＜0
g(x)<h(x)
よって｛h(x）ーg(x)｝のαからβまでの積分がC₁とC₂で囲まれた面積の値となる。（セの答）。

β（2b)<x<tの範囲で（x－b)、(x－2b)はともの正の値なので

g(x)ーh(x)＞０
よって｛g(x）ーh(x)｝のβからｔまでの積分がC₁,C₂、ｘ＝tで囲まれた面積の値となる。（ソの答）。