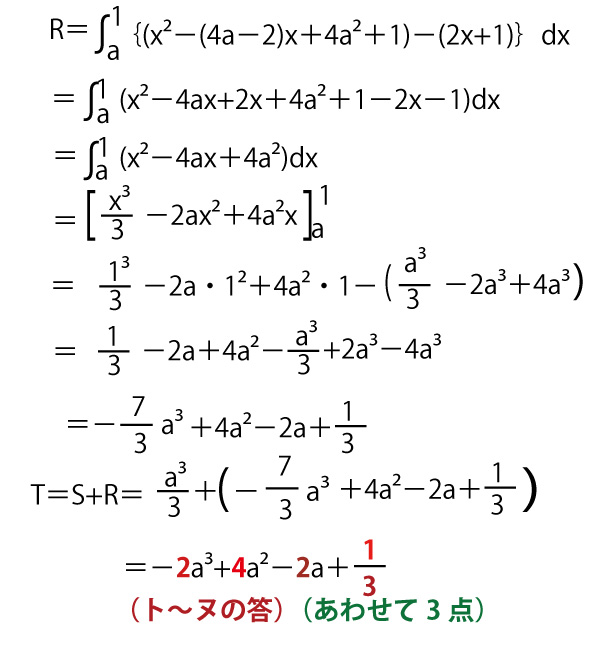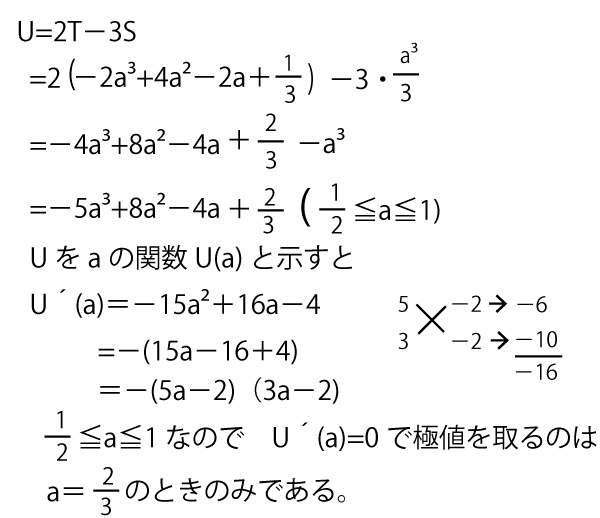2020年大学入試共通テスト「数学ⅡB」第２問［２］（微分・積分）問題・解答・解説
asakura
【解説】
（1）
Cに関して
ｙ´＝2x＋2
よって点（t、t2＋2t+1)における接線の傾きは2t＋2なので、接線ℓの方程式は
ｙ－（t2＋2t+1)＝(2t+2)(x－t)
ｙ＝(2t+2)x－t(2t+2)＋t2＋2t+1
y=(2t+2)x－2t2−2t＋t2＋2t+1
y=(2t+2)x－t2+1 (2t+2で2点）（１で2点）・・・・・
Dに関し
ｆ´（x）＝2x－4a＋2
点(s,f（s））での接線は、
ｙ－f(s)＝f´（s)(x－s)
yー（s2−(4a－2)s＋4a2+1)＝(2s－4a+2)（x－s)
y＝(2s－4a+2)(x－s)＋s2−(4a－2)s+4a2+1
y=(2s－4a+2)x－2s2+4as－2s＋s2−4as+2s+4a2+1
y=(2s－4a+2)x－s2＋4a2＋１ （2s－4a＋２で2点）（4a2+1で2点）‥‥
は同じ式を表しているので
傾きが等しいので、
2t+2＝2s－4a+2
2t=2s－4a
t＝s－2a…‥
ｙ切片が等しいので
－t2+1＝－s2＋4a2＋１
t2−1＝s2−4a2−1
t2＝s2−4a2‥‥
の両辺を2乗すると
t2＝（s－2a)2
t2＝s2−4as＋4a2‥‥
より
s2−4a2＝s2−4as＋4a2
－8a2＋4as＝0
2a2−as＝0
a(2a－s)=0
a>0なのでa≠０
よって2a－ｓ＝０
ｓ＝2a（コの答）
に代入して、ｔ＝０（ケの答）（ケコあわせて3点）
したがって、ℓの方程式は
ｔ＝０をに代入して
ｙ＝2x＋１（サシの答）（あわせて2点）
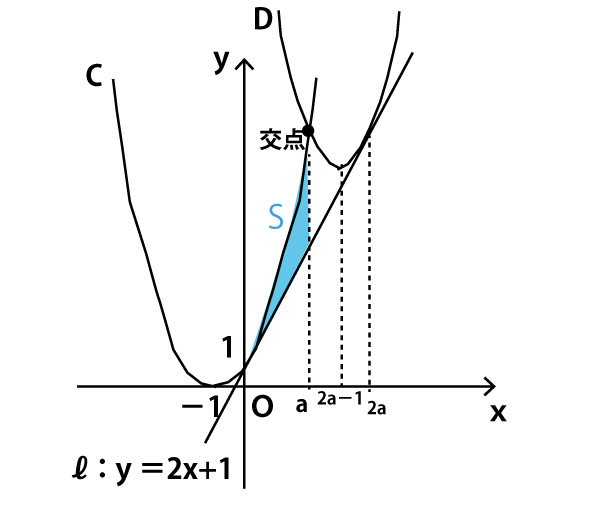
（2）
２つの放物線の交点のx座標を求める
ｘ2−（4a－2）ｘ＋4a2＋1＝x2＋2x＋1
（－4a＋2)x＋4a2=2x
－4ax+4a2＝0
a(x－a)＝0
a>0でa≠0なので x=a（スの答）
放物線Dは
ｙ＝x2−(4a－2)x＋4a2＋１
y=x2−2(2a－1）ｘ＋4a2+1
なので軸はｘ＝2a－1となる。
接線ℓも含めて図を描くと
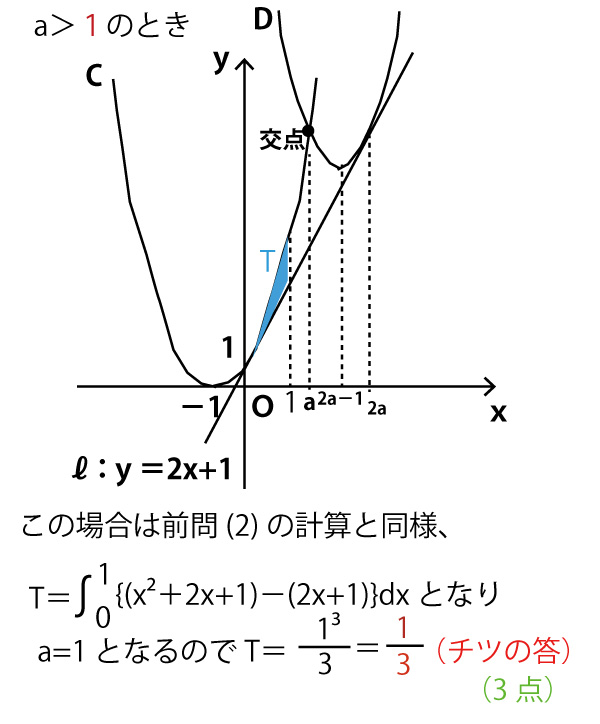
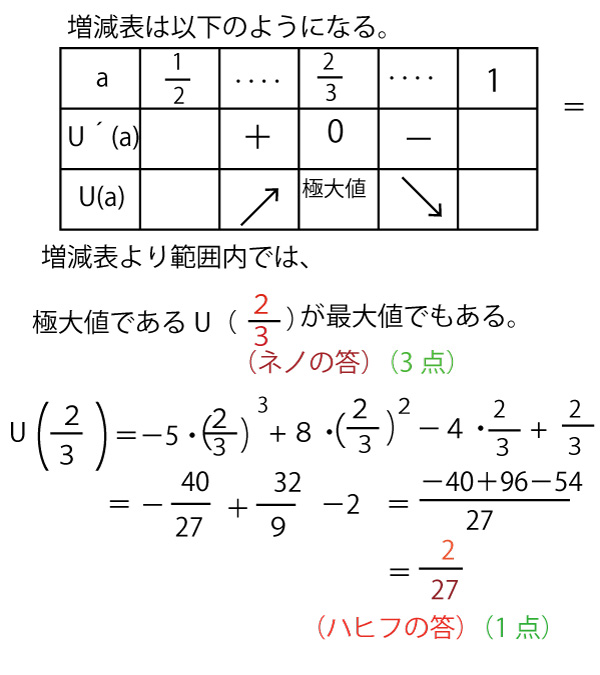
（3）
a＞１（タの答）（2点）のとき、下図のようにaの値に関係なくTは一定となる。
