2016年前期、千葉県公立高校入試「数学」第2問（5）（作図）解答・解説

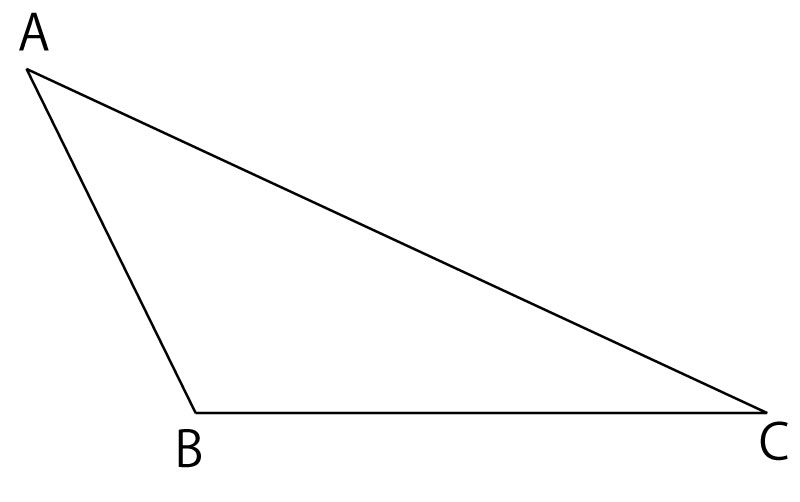
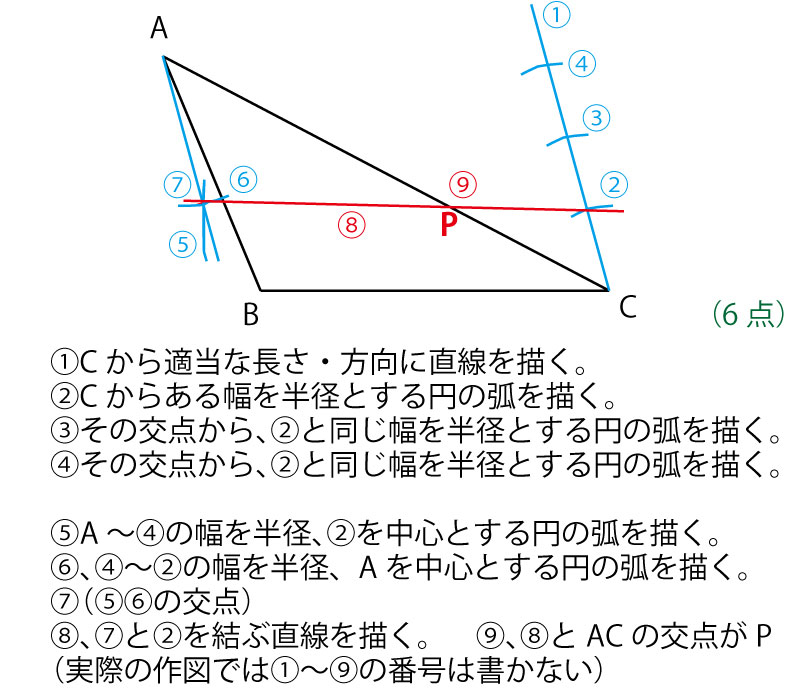
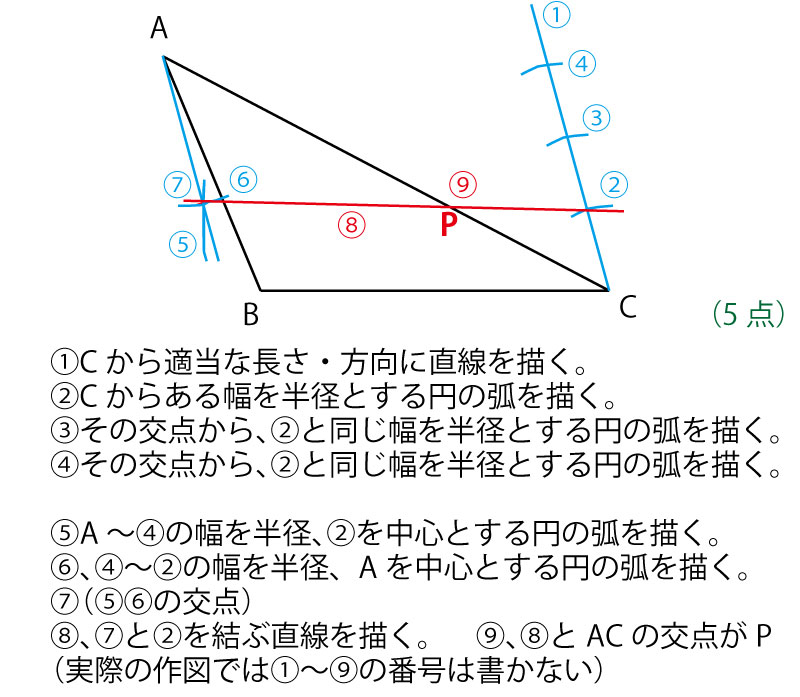
第2問（5）解答例１

（5点）

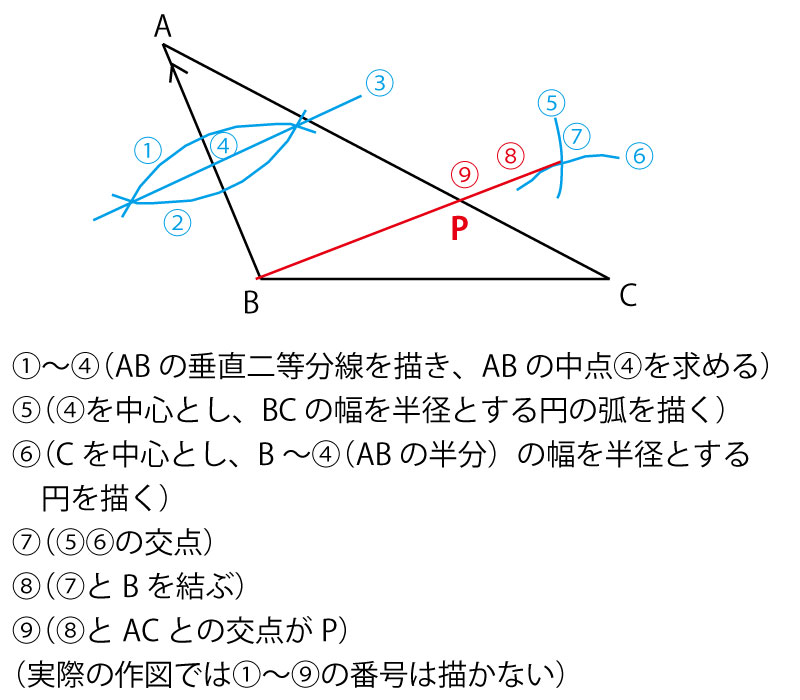
第2問（5）解答例２

【解説】
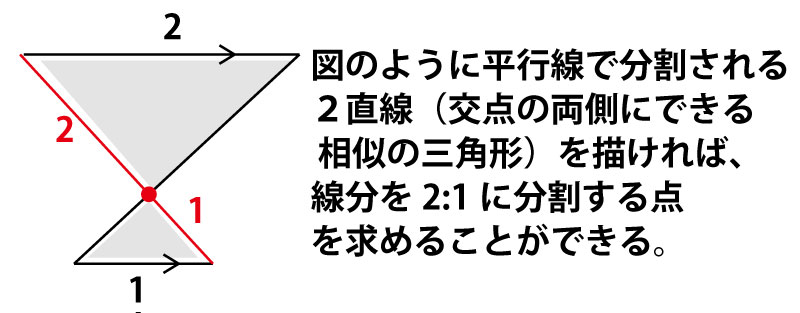
ACを１：１に分割する点（中点）ならば、垂直二等分線を求めればよい。しかしAP：PC＝2：1というように２：１に分割する点の作図をどうしたらよいのだろうか？
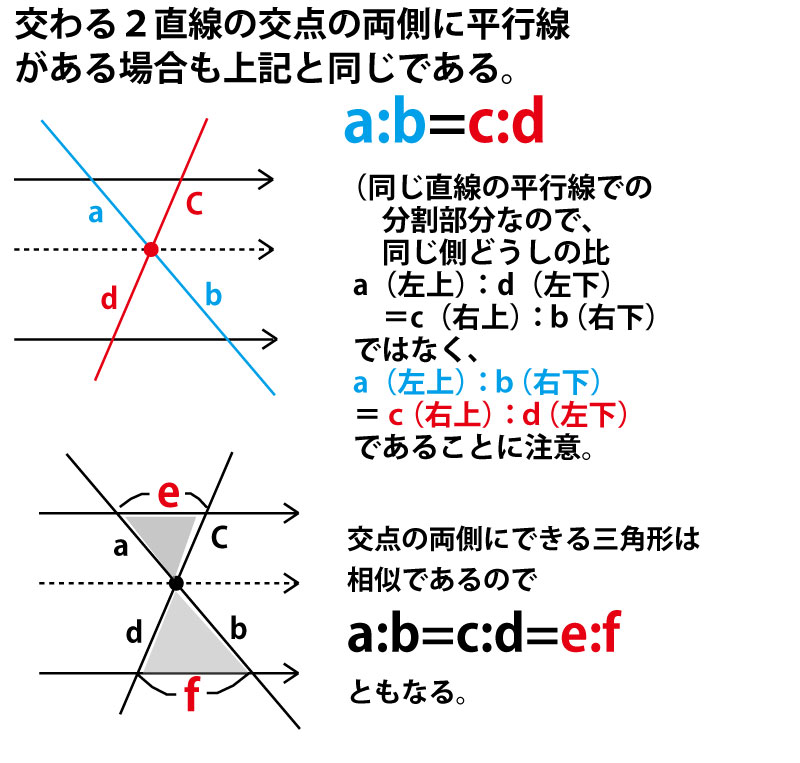
中２で学ぶ平行線と線分の性質と、中３で学ぶ相似な三角形のことを思い出してみよう。

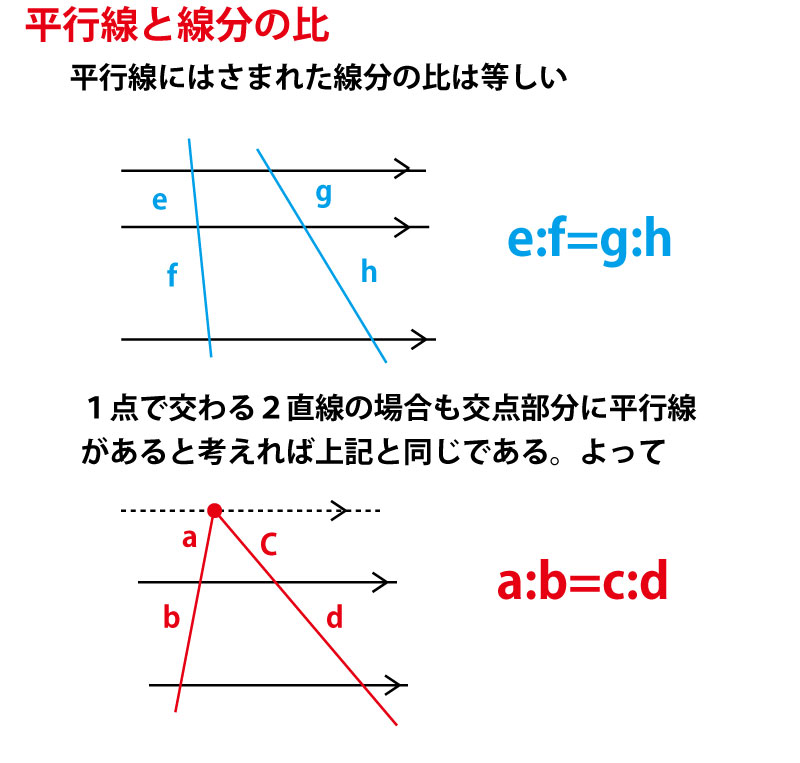
すると、平行線に挟まれる形で以下のような作図ができれば、ACを２：１に分割する点を求めることができそうである。

ちなみに、作図には平行線の作図（平行四辺形の作図）が必要になってくるので作図法をまとめておこう。

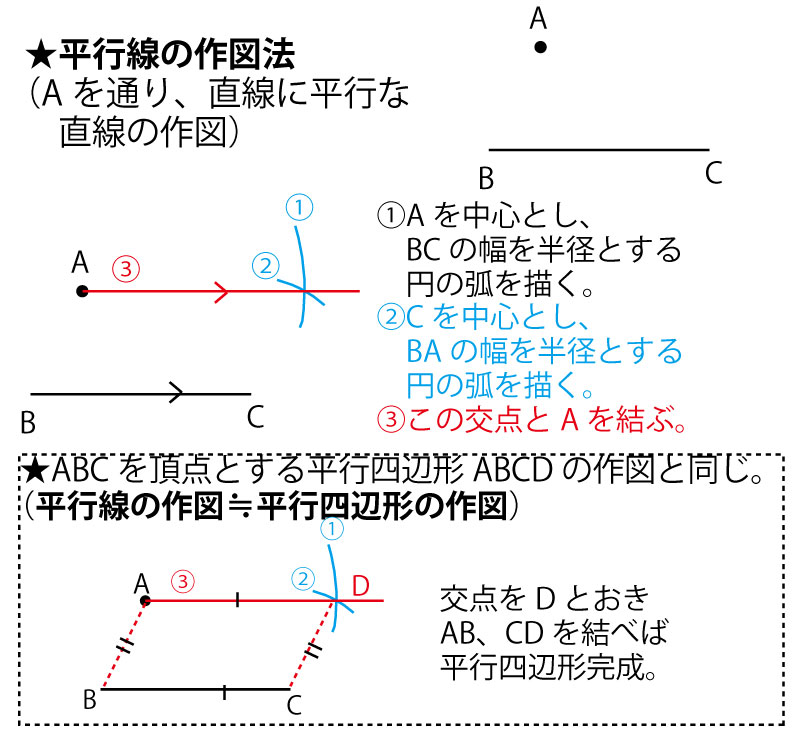
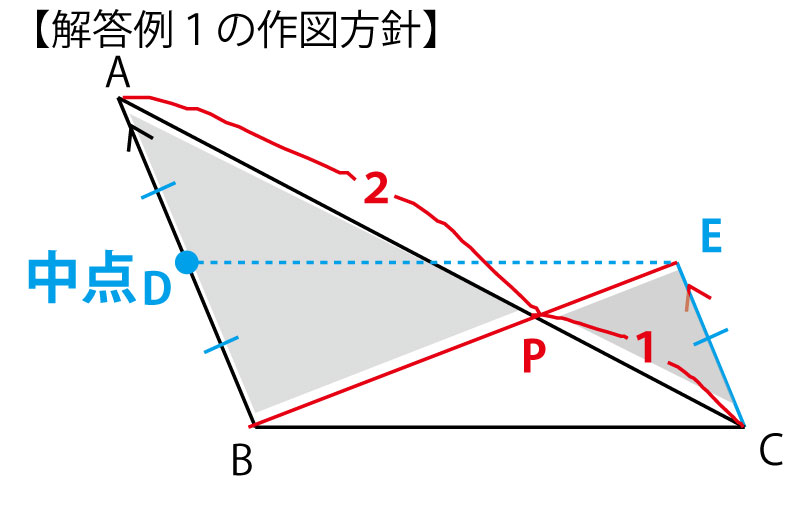
①ABの中点D２をABの垂直二等分線から求める。
②DBの長さとBCの長さの半径の円を使い、平行四辺形DBCEを作図すると、DB=CEとなる。
③するとAB：EC=2:1で、AB∥ECなので、EBを結ぶとEBとACの交点が
AP:PC=2:1の点Ｐとなる。

↓実際の作図
（実際の作図では作図方針に示した三角形や平行四辺形の線は描かれないが、最後にその発想があることを上下の図を照らし合わせて確認しておこう。）

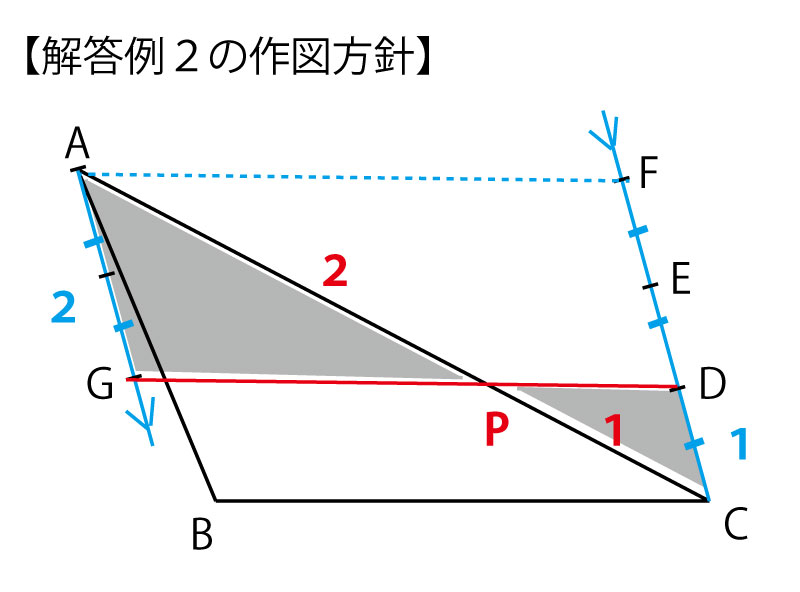
①CDから自由な方向に直線を描き、コンパスで同じ半径で円の弧を描くことを通じ、均等に１：１：１の間隔で並ぶD・E・Fを描く。
CD=DE=EF
②DFDを３つの頂点とする平行四辺形AGDEを描く（Gの位置を決める）。平行四辺形の対辺は等しいのでAG=FD。FD=2DCいり、AG:DC=2:1。
また平行四辺形なのでAG∥DC(FC)。
③GとDを結んだGDとACの交点をPとするとAP:PC=2:1。
↓実際の作図
（実際の作図では作図方針に示した三角形や平行四辺形の線は描かれないが、最後にその発想があることを上下の図を照らし合わせて確認しておこう。）