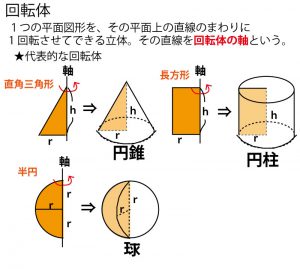
2015年前期、千葉県公立高校入試「数学」第2問（4）（確率）解答、解説

2015年2月12日（木）に2015年前期、実施された千葉県公立高校入試「数学」第２問（４）（確率）の問題・解答・解説です。入試問題は白黒ですが、画面上なので一部カラーにしました。配点と千葉県教育委員会が発表した正答率（無答率）を付記します。

第2問（4）（確率）（5点）（正答率21.1%(無答率13.0%)）

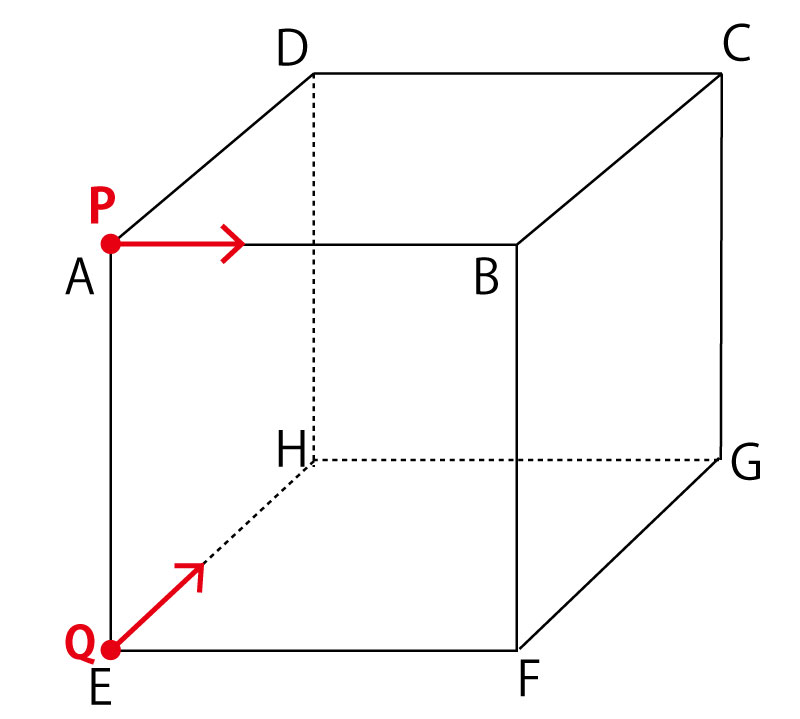
図のように、点A、B、C、D、E、F、G、Hを頂点とする立方体があり、この頂点上を移動する2点P、Qがある。
大小２つのさいころを同時に1回投げる。点Pは、点Aを出発点として、大きいさいころの出た目の数だけ、→B→C→D→A→B→Cの順に移動し、点Qは、点Eを出発点として、小さいさいころの出た目の数だけ、→H→G→F→E→H→Gの順に移動する。
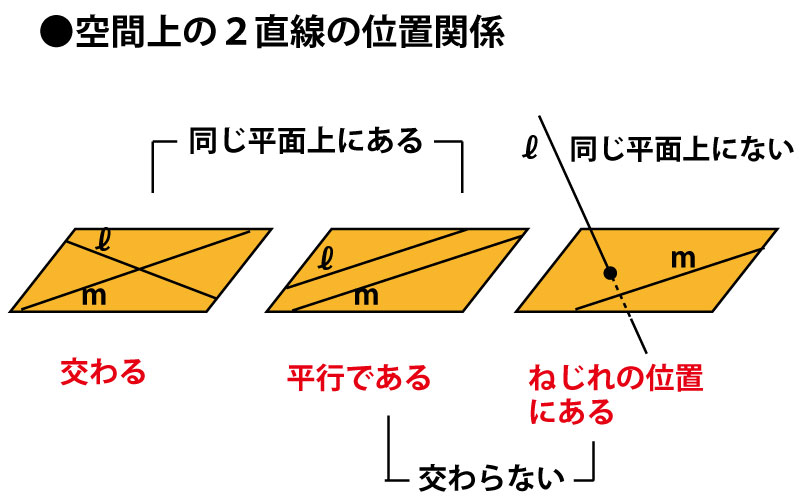
このとき、直線PQと直線CGが、ねじれの位置にある確率を求めなさい。ただし、さいころをさげるとき、１から６までのどの目が出ることも同様に確からしいものとする。

[next_p]