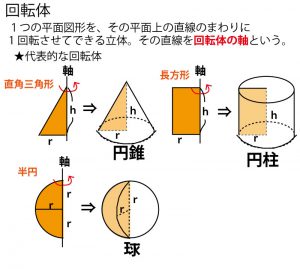
2015年前期、千葉県公立高校入試「数学」第2問(4)(確率)解答、解説
解説
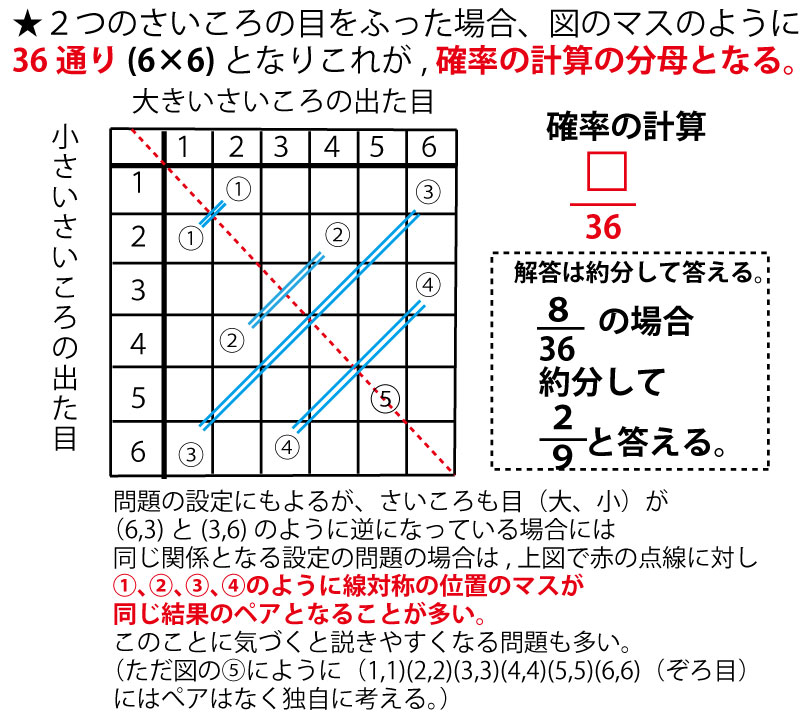
千葉県では、大小2つのさいころを同時に1回投げて、出た目の数に関しておきる事象の確率を求める問題が多い。他の入試でもこの出題は多い。そこでその場合の基本点を確認しておこう。まずは、縦・横、6×6のゴバン目ますを描いて考えるのが基本となる。
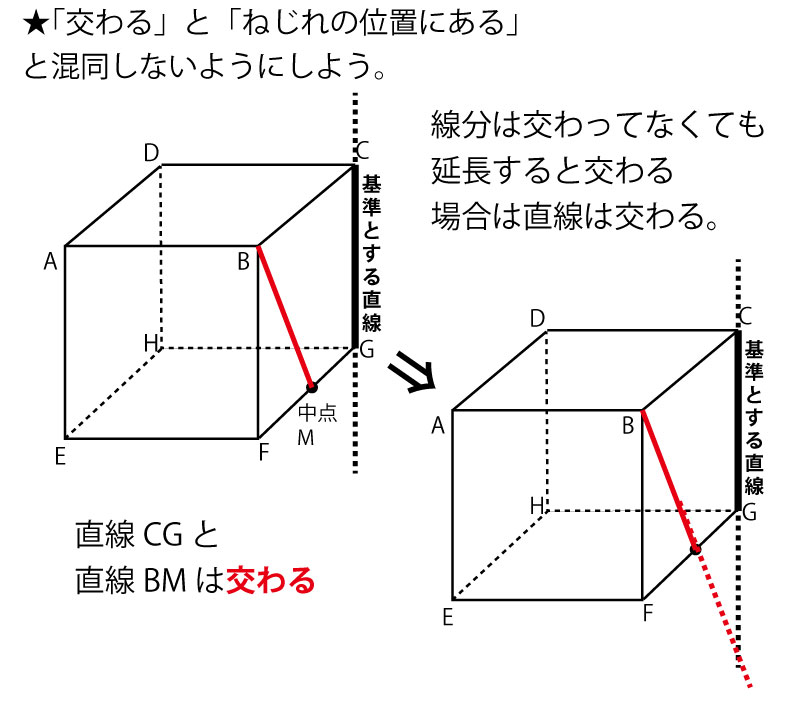
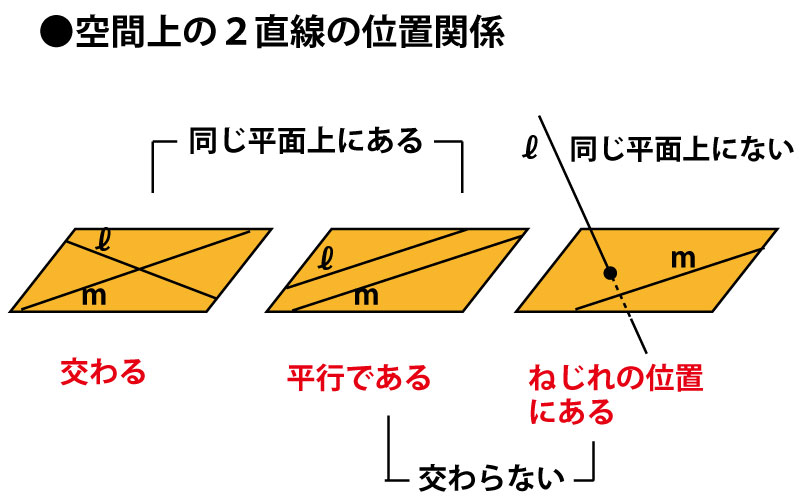
次にこの設問で問われている「ねじれの位置にある」とはどういうことか、空間での2直線の位置関係を確認しよう。
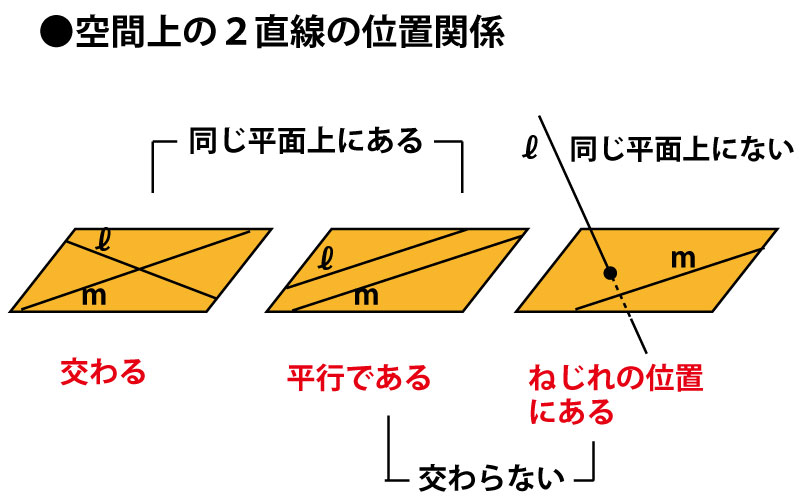
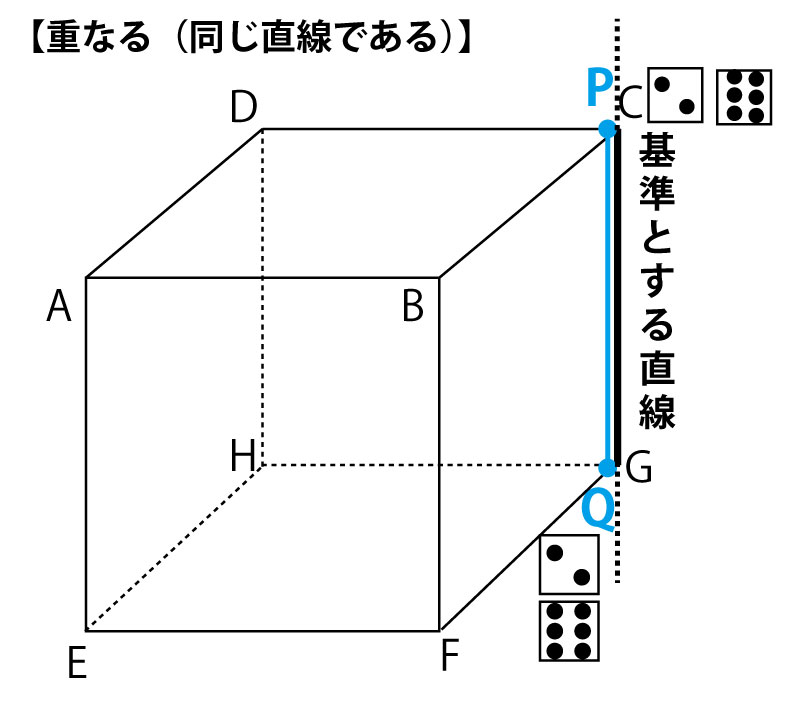
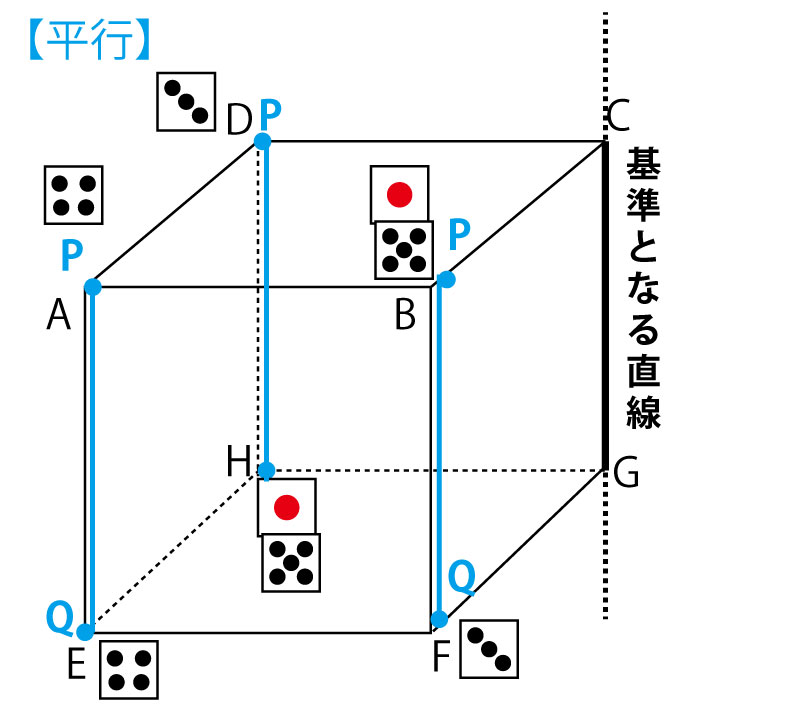
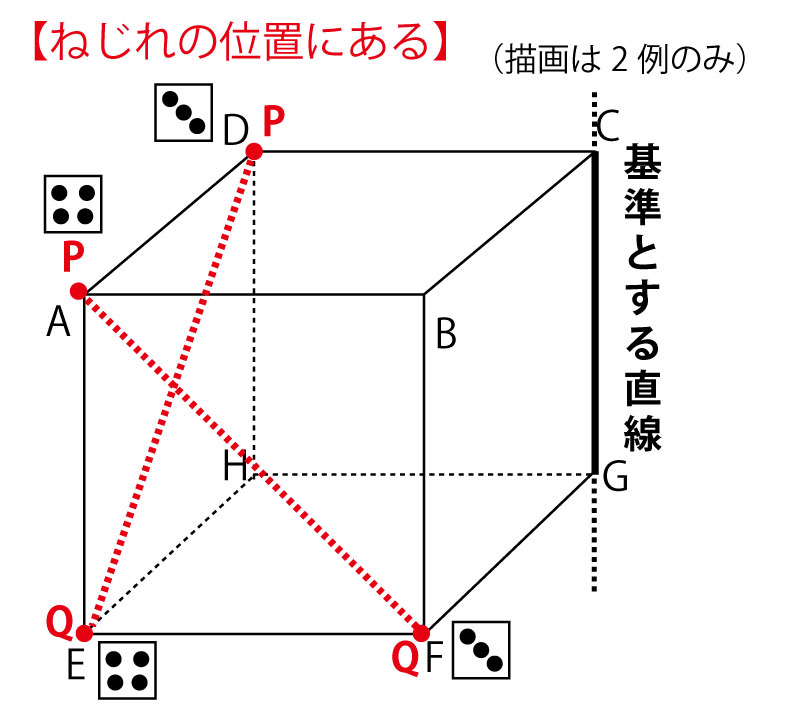
この3者の関係は立方体(さいころなど)の12本の辺(を両側に延長した直線)において、ある辺(を両側に延長した直線)を基準として確認するとわかりやすいし、立方体の辺の関係を聞く問題もズバリ出題されるので確認しておこう。立方体の12本の辺(を両側に延長した直線)を分類すると、基準と同じ直線(重なる)が1本、平行が3本、交わるが4本、ねじれの位置にあるが4本となる。
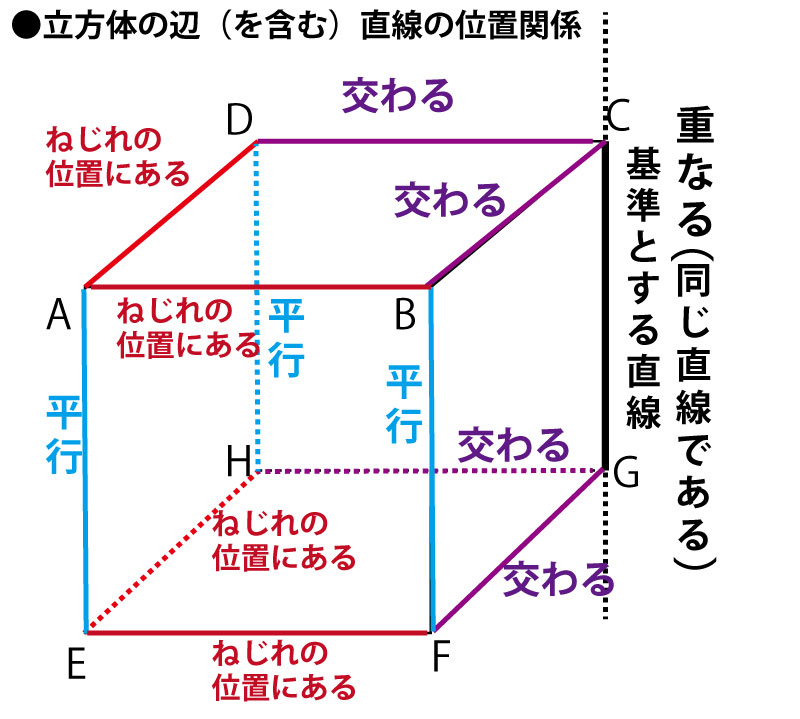
さて、辺ではないが、以下の点もよく勘違いするので確認しておこう。
それでは、これから本設問の点P、Qの動きと直線PQの位置を確認してみよう。
まずさいころの目の出方とPQの位置は以下のようになる。Pは上の面の4頂点を、Qは下の面の4兆点を移動する。
「1の目と5の目」「2の目と6の目」は同じ位置に来ることを確認しよう。
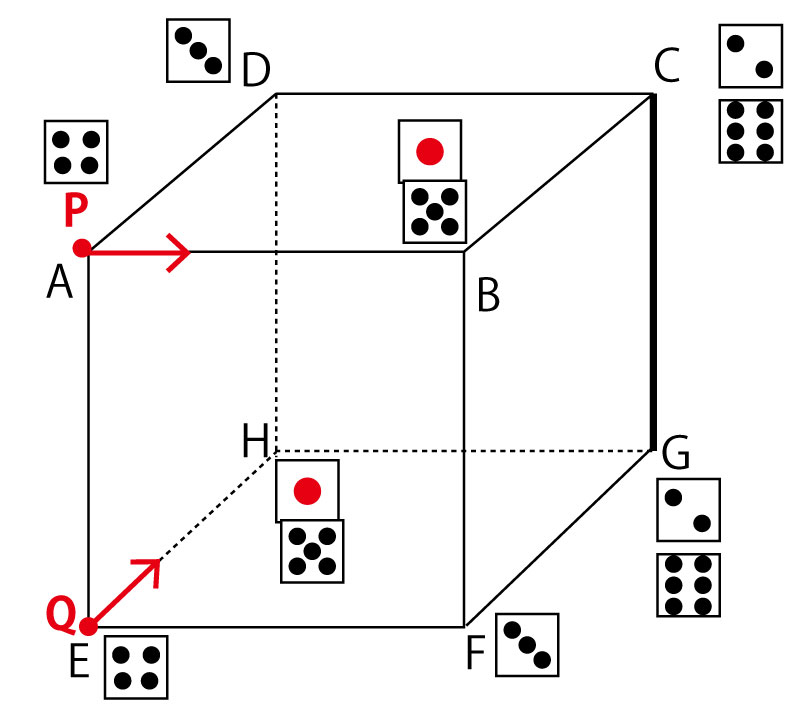
次に基準とする直線CGとの位置関係とその時の目の出方を確認しよう。(先ほど確認した立方体の辺の問題である)
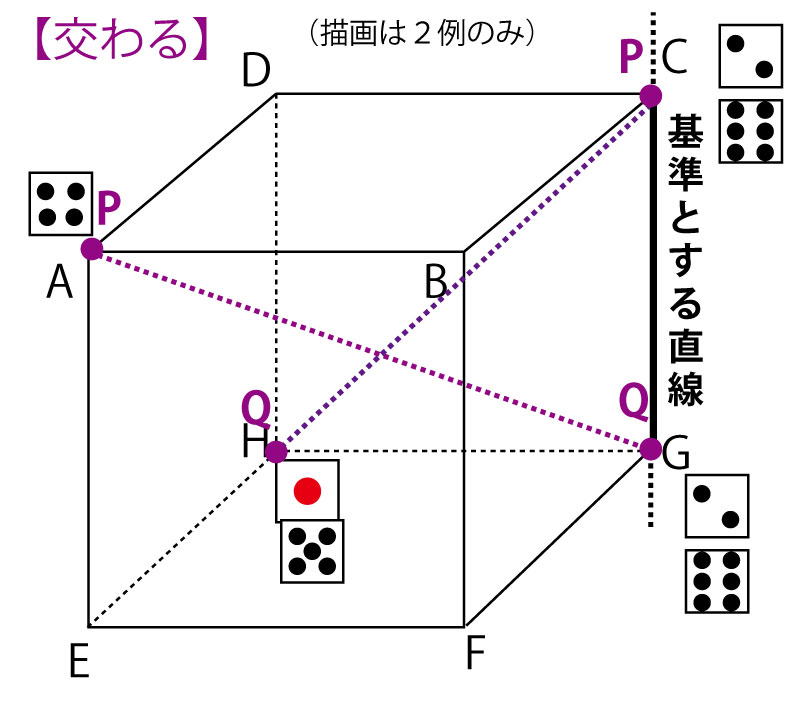
【交わる】形となるPQはもっと多いが図が見えにくくなるので上図では2つのみ示した。
PがCの位置に来る(目は2か6)場合は、Qはどの位置にあろうとも、必ず交わる。
同様にQはGの位置に来る(目が2か6)場合は、Pがどの位置にあろうと必ず交わる。
このことに気づけば、全部を図示しなくても、どういう場合かを理解できる。
(ただし、PがCかつQがGの場合は「交わる」ではなく重なる(同じ直線である)となる。)
【ねじれの位置にある】形となるPQはもっと多いが図が見えにくくなるので上図では2つのみ示した。全部を図示して数えようとしても、図がゴチャゴチャになり間違えやすい。そこで「ねじれの位置」は「重なる」「平行」「交わる」以外のものだという消去法で考える。
それではいよいよまとめに入ろう。1と5の目、2と6の目が同じ結果なので、それを合体した変化パターンのゴバン目表を書き、上記「重なる」「平行」「交わる」がどのマスに来るか書き込む。「交わる」はP、Qのいずれかが「2,6」の位置であるので、「2,6」の位置の縦横列のマスに位置する。またその縦列。横列が重なったところが「重なる」となる。
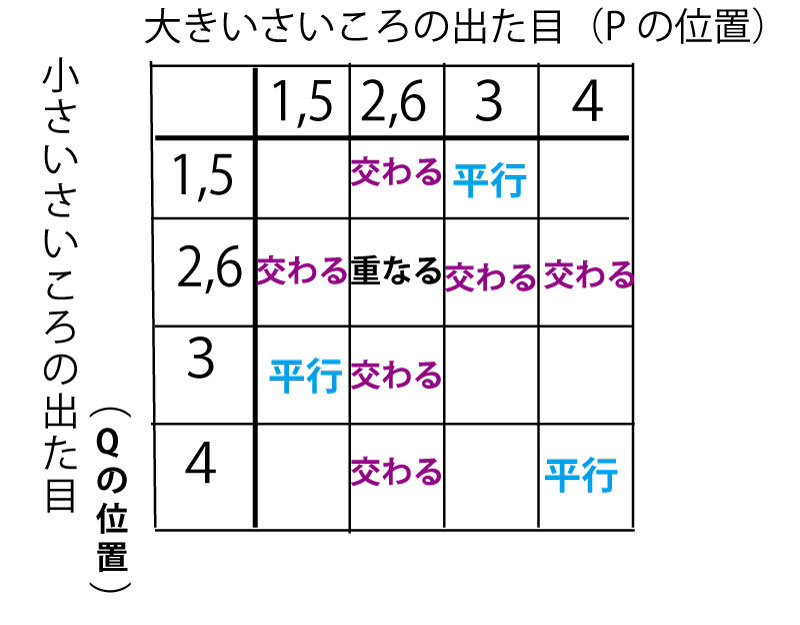
この表で空白部分が消去法で「ねじれの位置」である。「1,5」「2,6」の行・列は場合の数が2であり、両者が重なったところは2×2で場合の数が4であることに気をつけて、空白に場合の数を書きこんでみよう。
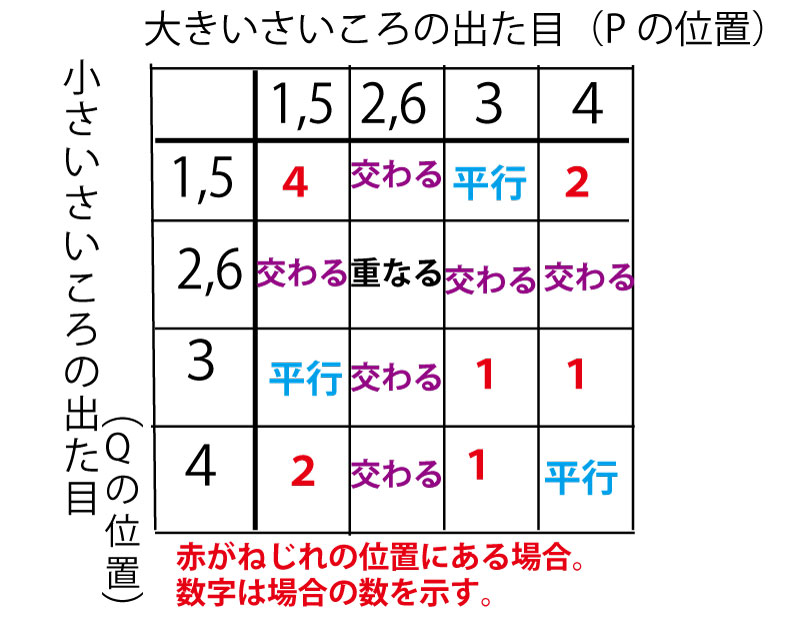
若干変化したパターンのゴバン目表であるが、やはり線対称の関係になっていることも確認してみょう。
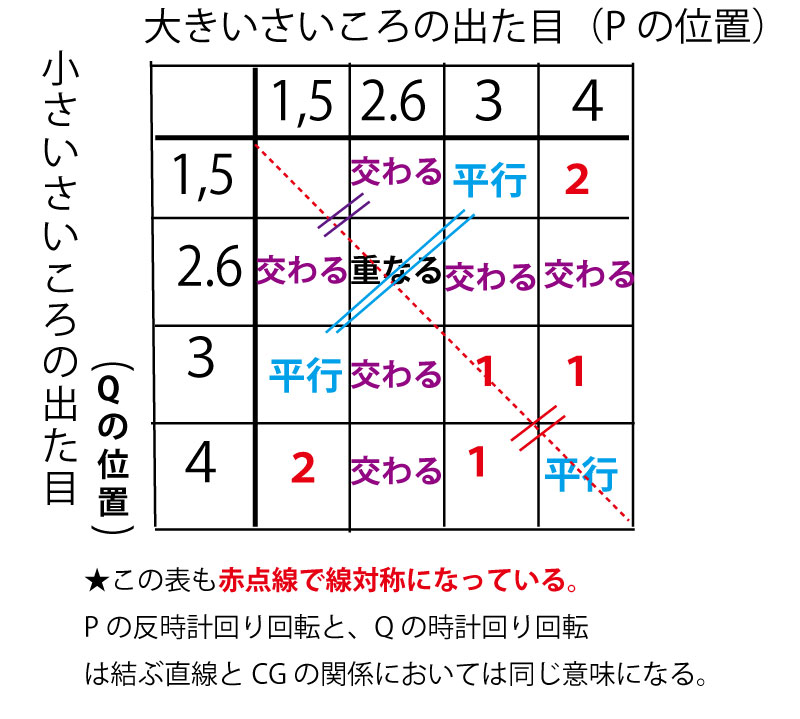
最後、空白に書き込んだ「ねじれの位置」になる場合の数を足していき、場合の数の総数36で割ると答えとなる。