2021年、千葉県公立高校入試「数学」第4問(図形の証明)(配点15点)問題・解答・解説
2021年7月14日 予備校講師・船橋市議 朝倉幹晴
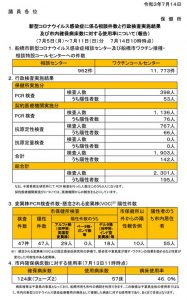
2021年2月の千葉県公立高校入試「数学」の第4問(図形の証明)の問題・解答、そして私(朝倉幹晴)が作成した解説です。千葉県教育委員会が発表した各問の正答率(無答率)も付記しました。ご活用ください。
2021年第4問(15点配点)
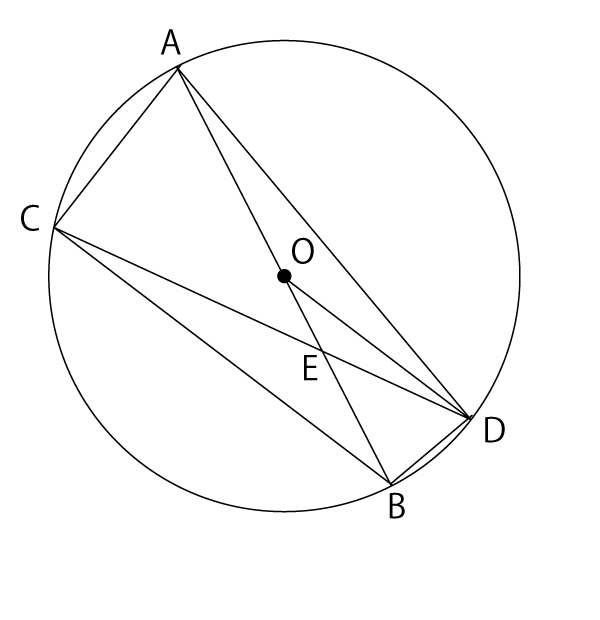
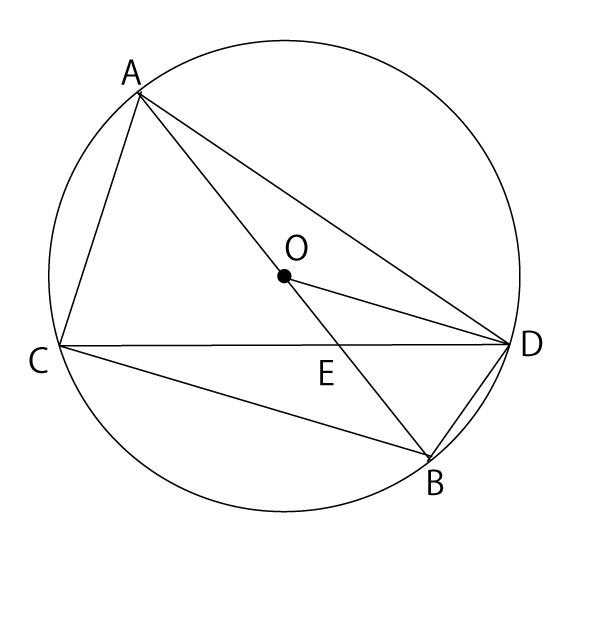
図のように、線分ABを直径とする円Oがある。![]() 上に、2点A、Bとは異なる点Cをとり点Cと2点A、Bをそれぞれ結ぶ。また、点Cを含まない
上に、2点A、Bとは異なる点Cをとり点Cと2点A、Bをそれぞれ結ぶ。また、点Cを含まない ![]() 上に、点DをCB∥ODとなるようにとり、点Dと3点A、B、Cをそれぞれ結ぶ。線分OBと線分CDの交点をEとする。
上に、点DをCB∥ODとなるようにとり、点Dと3点A、B、Cをそれぞれ結ぶ。線分OBと線分CDの交点をEとする。
このとき、次の(1)(2)の問いに答えなさい。
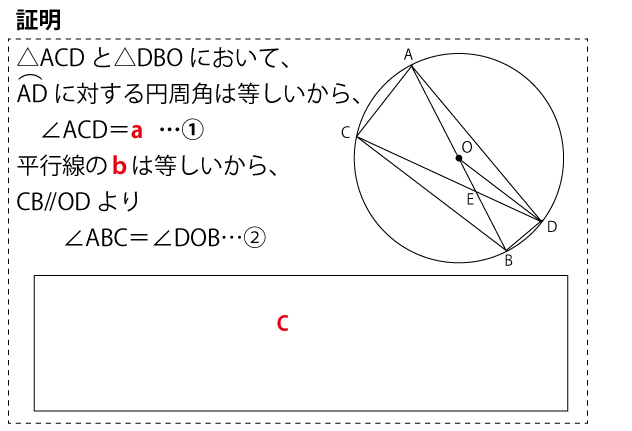
(1)△ACD∽△DBOとなることの証明を、![]() の中に途中まで示してある。
の中に途中まで示してある。
a (2点)(正答率88.7%(無答率0.3%)、b(2点)(正答率88.6%(無答率0.3%)に入る最も適当なものを、選択肢のア~カのうちからそれぞれ1つずつ選び、符号で答えなさい。
またc(6点)(正答率6点評価37.2%、3点評価3.9%(無答率30.3%))には証明の続きを書き、証明を完成させなさい。
ただし、![]() の中の
の中の![]() 、
、![]() に示されている関係を使う場合、番号の
に示されている関係を使う場合、番号の![]() 、
、![]() を用いてもかまわないものとする。
を用いてもかまわないものとする。
選択肢
ア∠ABC イ∠AED ウ∠DBO エ錯角 オ同位角 カ対頂角
(2)AO=2cm、CB=3cmのとき、線分BDの長さを求めなさい。
(5点)(正答率3.4%(無答率36.7%))
[next_p]