2021年、千葉県公立高校入試「数学」第4問（図形の証明）（配点15点）問題・解答・解説

2021年7月14日 2021年7月15日

asakura

【解説】
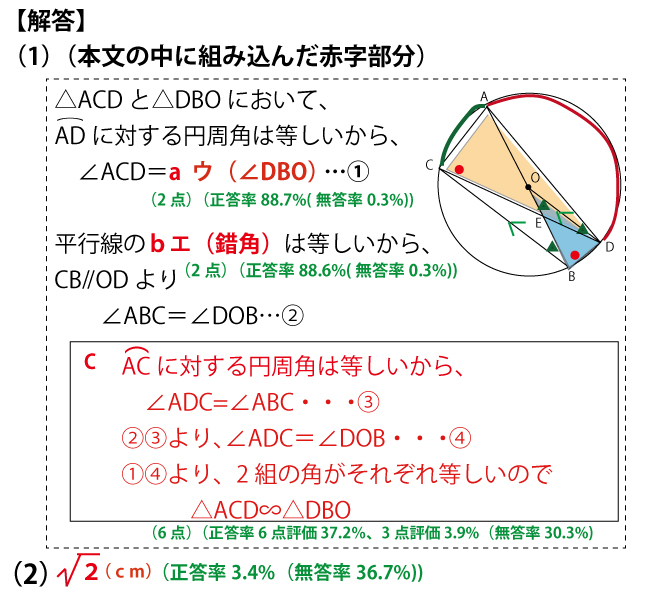
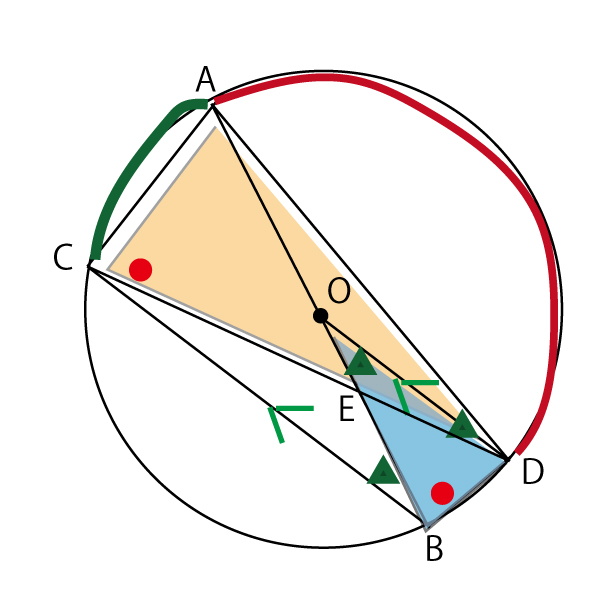
（1）上記図の色分けを確認しながら、じっくり読んで理解してほしい。図では注目し相似を証明する２つの三角形を青と肌色で塗って強調した。
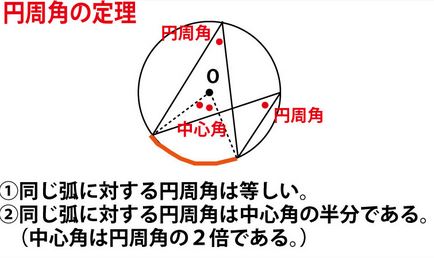
赤でなぞった弧ADに対する円周角を●と表記した。aの答がウ（∠DBO）となることを確認してほしい。

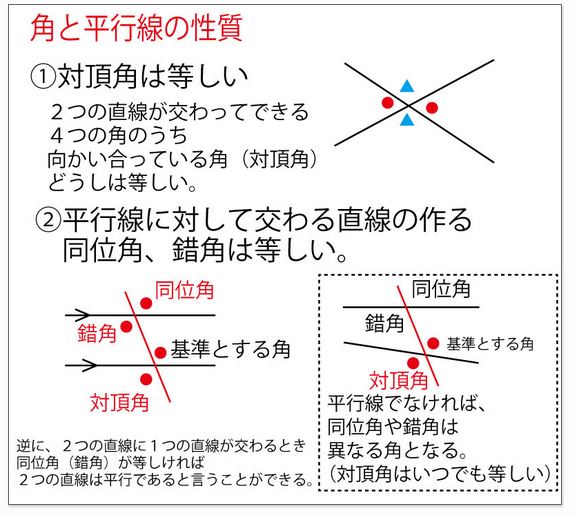
　次に平行線CB∥ODを→で表記し、それを横切るOBとの間の角を▲で表記した。すると∠ABC＝∠DOBの関係はエ（錯角）とわかる。

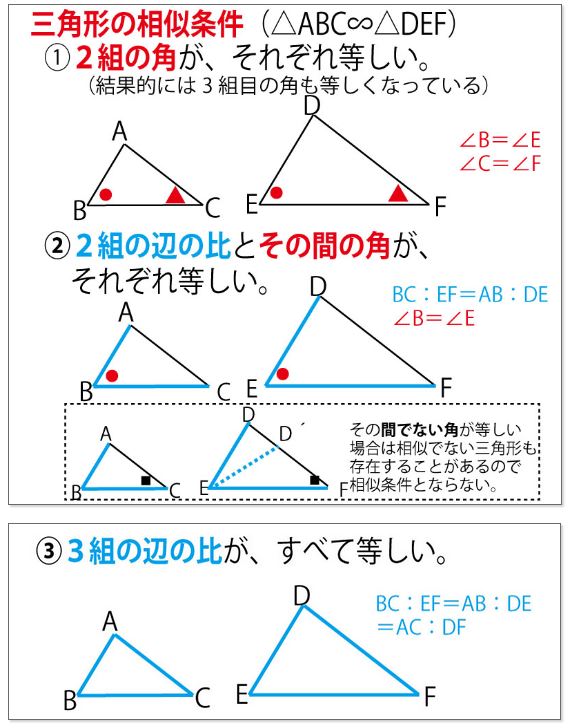
最後にｃの空欄部分を埋めて証明を完成させる。証明の目的は、色塗りした２つの三角形の相似であり、次の三角形の３つの相似条件をいずれかを使って証明する。

ただ本設問では、辺の比に関する記述がないので、「2組の角がそれぞれ等しい」条件を使うだろうと推測できる。
（三角形の相似の証明に関しては千葉県公立高校入試の過去15年の出題比率としても、「2組の角がそれぞれ等しい」条件を使う場合が8割以上である）

もう一度、証明の流れの図を拡大して確認してみよう。

本文に書いてある∠ABC＝∠DOB（▲）のうち、∠DOBは相似を証明すべき水色の三角形（△DBO）の角であると図で確認できる。しかし、∠ABCは相似を証明すべき三角形の角ではないので証明すべき肌色の三角形の角との関係に変換できないかを考える。すると図の緑線で太く塗った弧ACに注目し、円周角の定理を使うと、∠ABC＝∠ADCで、相似を証明すべき肌色の三角形（△ACD）の角となる。以上の流れを整理し、解答のような証明の流れとなる。

（2）

正答率3.4%（無答率36.7%)、つまり30人で1人だけができる、中３としては難問で、できなくても気にする必要はない。ただ、できたほうがよりうれしいので以下解説します。

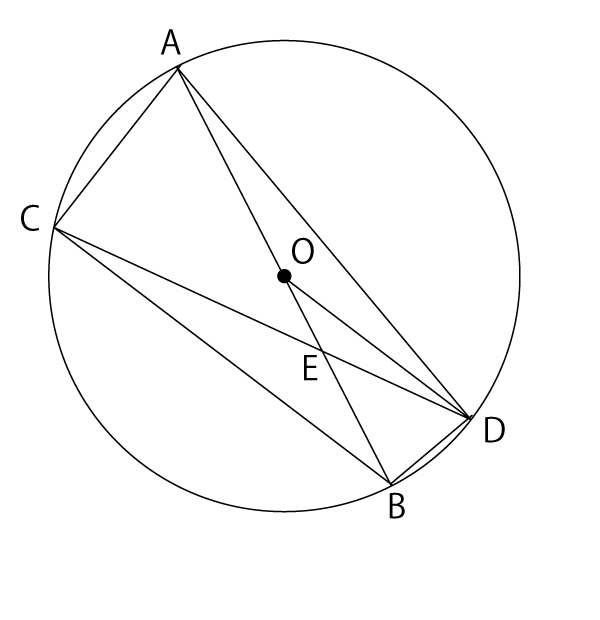
問題に最初に与えられた数値と、長さを求めるべき線分を書き入れてみる。

これだけでは情報が不足するので、わかる線分の長さや角度（直角）などを書きいれてみる。
線分の長さのヒントは以下にことに注目する。
１、円の中心と円周を結ぶ線分はすべて半径であり、AO＝２と同じ長さである。
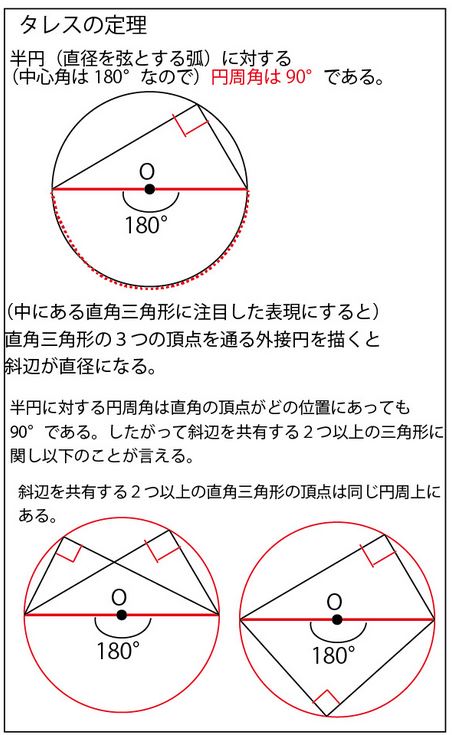
２、直径を弦とする弧に対する円周角は90°（タレスの定理★（最後に解説あり））であり、その角を含む直角三角形で三平方の定理を使う。

また、数学の問題は前の小問の答が、次の小問を解くヒントとなることが多いので（1）で証明した「△ACD∽△DBO」を使うはずなので、その部分も塗って強調してみる。すると以下の図まで数値がわかる。

（なお（1）で証明した△DBOは、2辺OB、ODは半径でOB＝ODの二等辺三角形とわかる。したがって相似である△ACDも二等辺三角形であり、等しい2辺を｜で示してある。）

相似の三角形で△ACDはACの長さはわかり、△DBOではOD（OB）の長さはわかり、DBが求めるべき長さである。したがって△ACDでAD（CD）の長さがわかる、あるいはその長さがDBとの関係で示す数式が求められれば、相似比を使ってDBの長さを求めることができそうである。そこで直角三角形ADBに注目し、DBをｘとし、ｘを使ってＡＤを示してみる。

ＡＤがｘを使った式で示すことができたので、相似比を使って求めてみる。

（他にも解答にいたる方法はあり、他の方法でも結構です。）

★図形の証明を様々な角度から理解したい方には、私が千葉県を含む７都府県の高校入試問題を解説した小冊子「図形の証明」（330円）をご覧ください。以下のようにアマゾンでご購入いただける他、私と直接会う機会がある方は、直接言ってくだされば、家にあるストックからお売りできます。
アマゾン取りつかい朝倉幹晴著書一覧（「図形の証明」他）