2019年前期、千葉県公立高校入試「数学」第3問（二次関数）問題・解答・解説

第３問解答（計15点）

解説

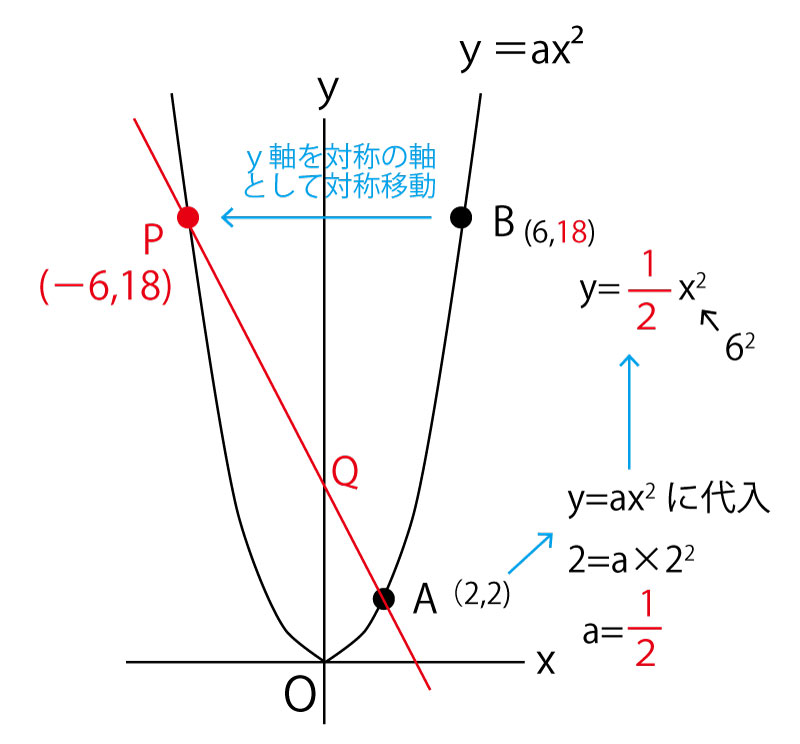
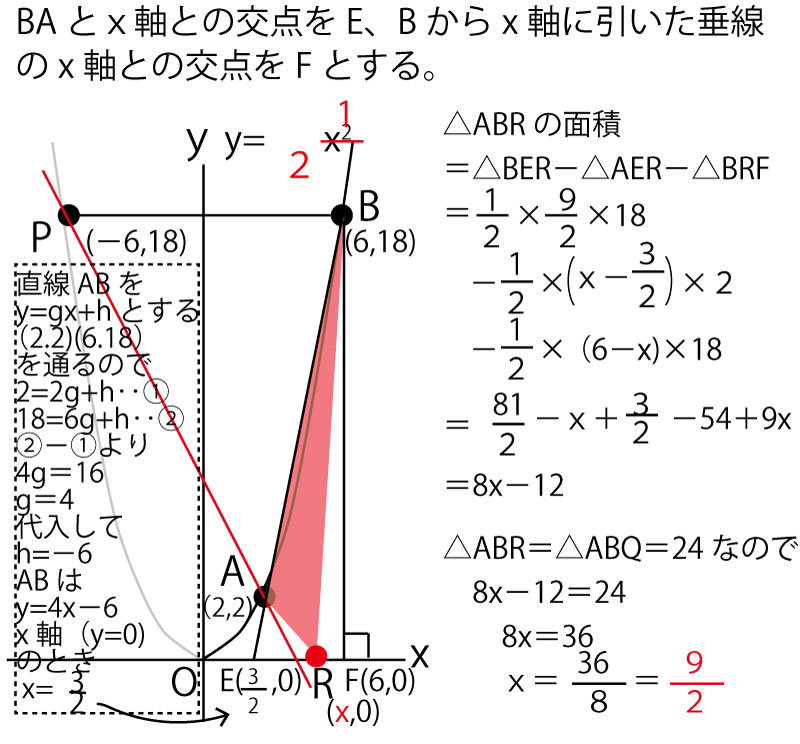
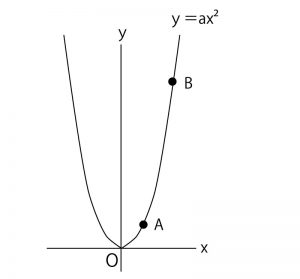
（1）上図の中にも示したようにA（2，2）をｙ＝ax²に代入する。2=a×2²。a=1／２

上記の図の流れで、P（－６、18）とわかるので、直線APはA（2，2）、P（－６、18）を通る直線である。
直線APの式をy=cx+dとすると（ｙ＝ax+bとしてもよいが、設問（1）での記号と区別するためc,dとした）
（2，2）を通るので　2=2c+d・・・[１]
（－6,18)を通るので、18＝－6c+d・・・[２]
[１]－[２]より　－16＝8c   c=－２
[１]に代入し、２＝２×（－2）＋ｄ　ｄ＝６
直線APの式は　ｙ＝－2x+6
点Qは直線APとｙ軸の交点、つまり、y切片なので　６

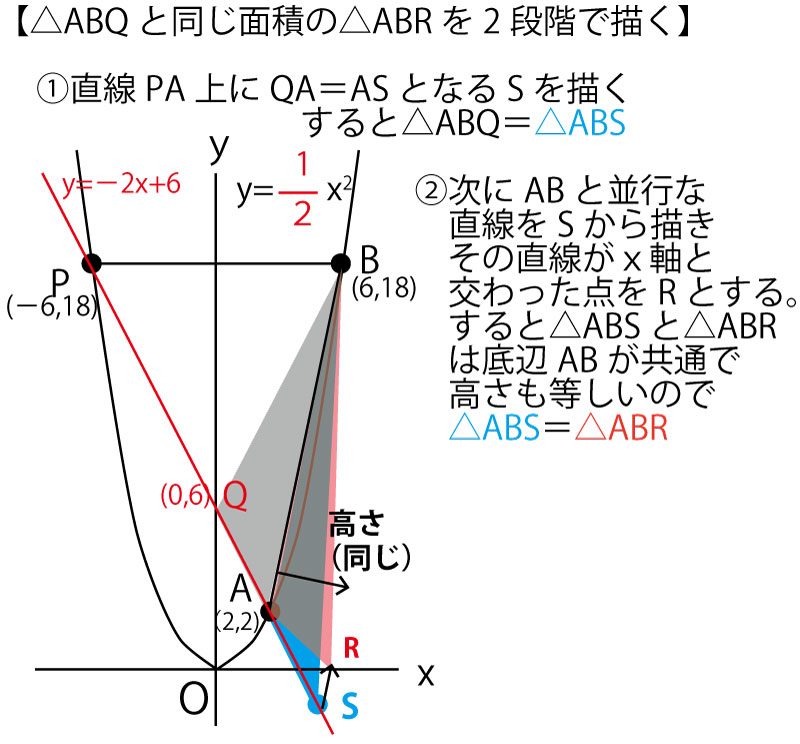
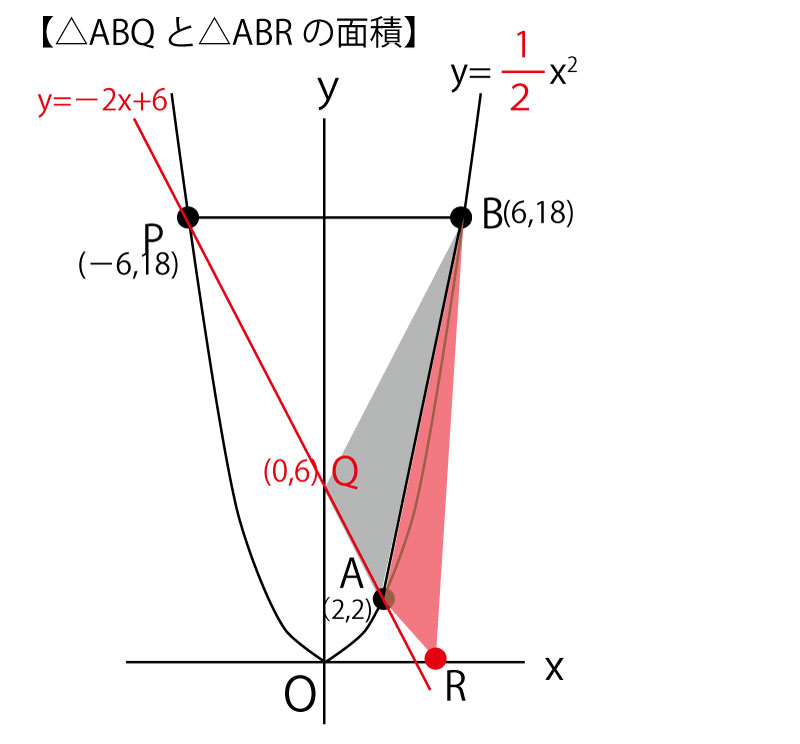
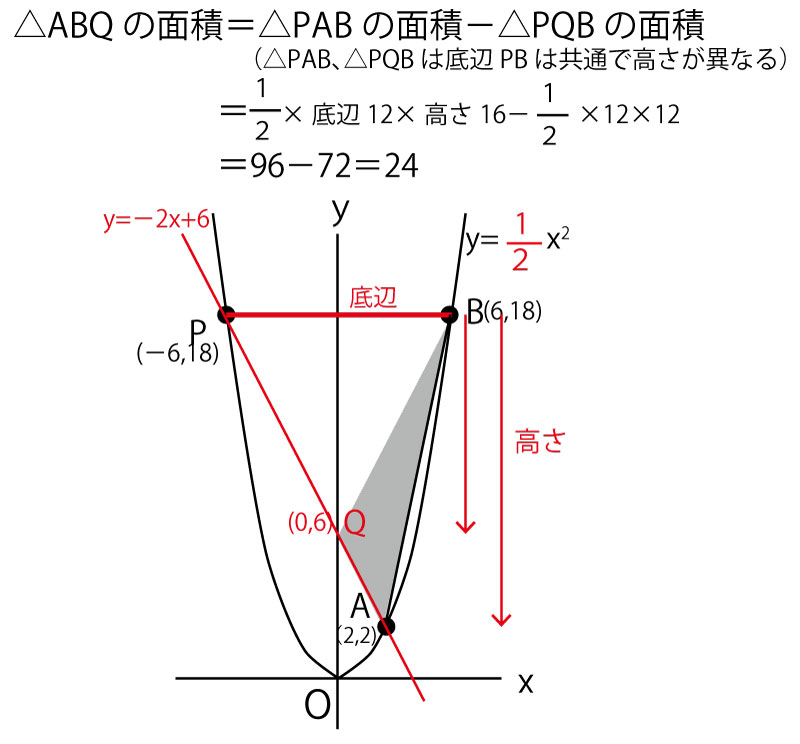
三角形などを同じ面積で変形させて考えることを「等積変形」という。その発想を使って解くと以下のように解くことができる。

別解（上記の等積変形のようは発想が思いつかなかった場合、三角形の面積を工夫して求める）