2016年前期、千葉県公立高校入試「数学」第2問（4）（確率）解答・解説

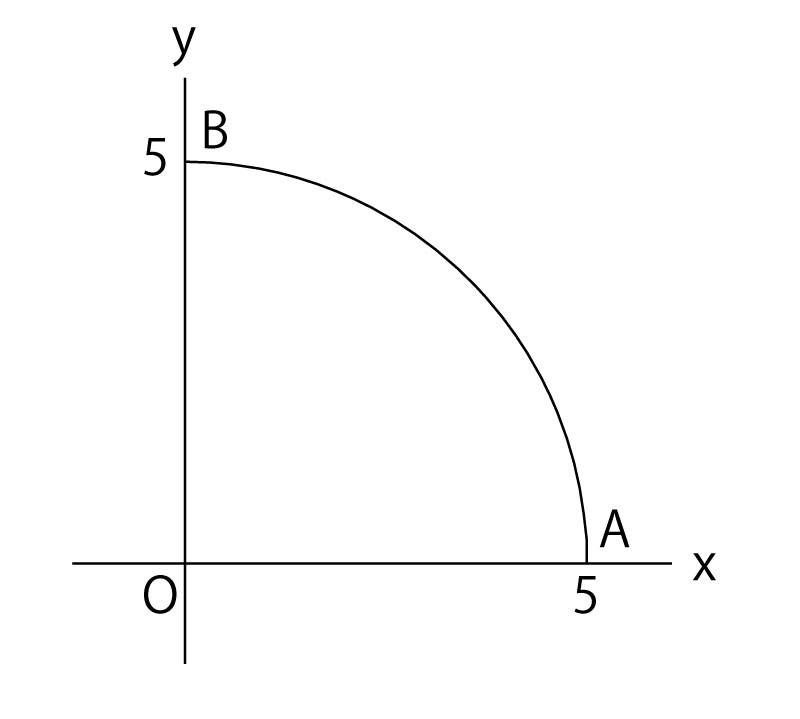
さいころの目の出方と座標。

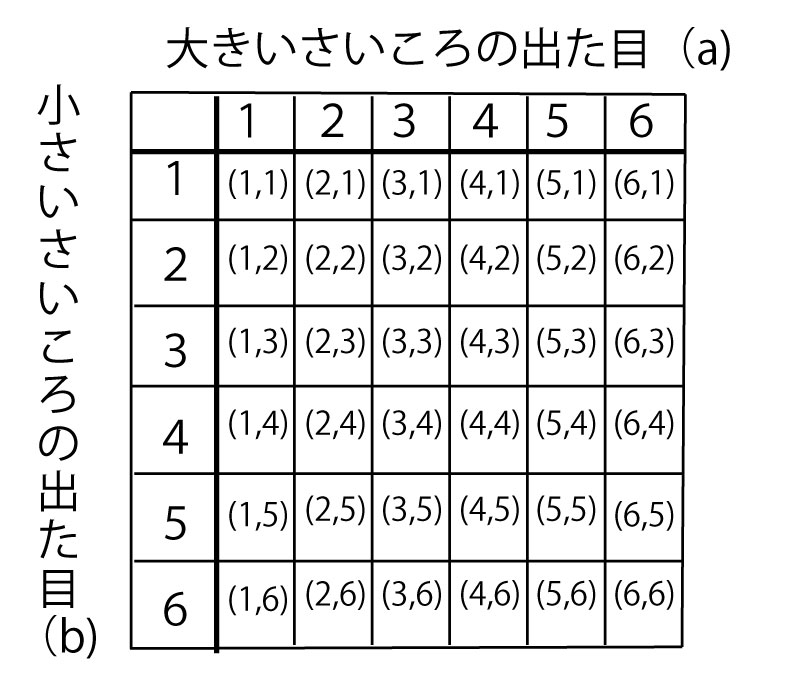
この上表は実際に試験時間中に丁寧に書いていると時間が足りなくなるので頭の中で処理する。
そして実際は、下図のよういに出題図のおおぎ形の中に点をうち、いくつの点がおおぎ形内部と円周上にあるかを書き込み図の中で数を確かめることを速やかに行う。

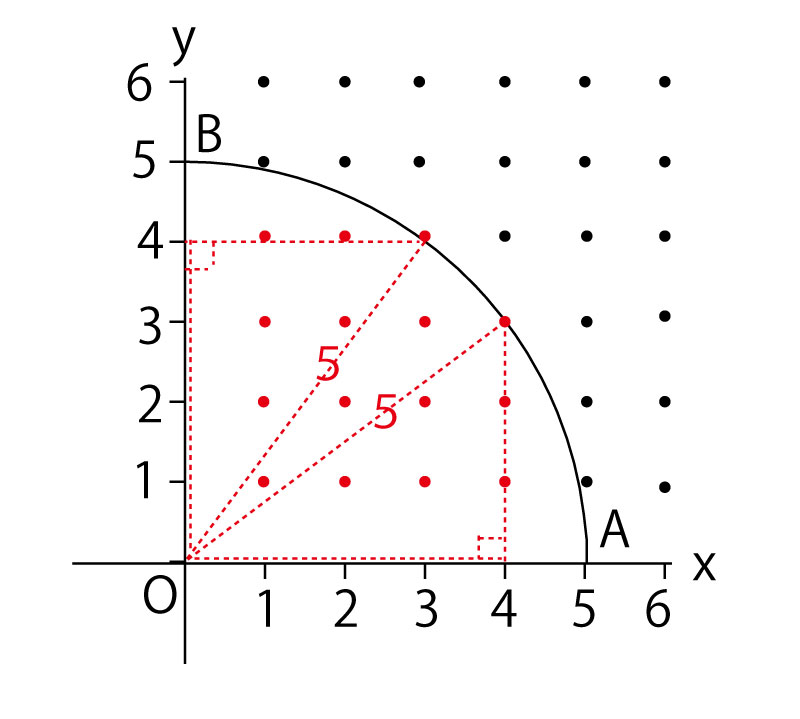
15個の赤点●が目的の点であり15個である。
図中で点線で直角三角形を描いた部分は
３²＋4²＝５²
(9＋16＝25）
となり、斜辺が５で半径となるので円周上にあることが確認できる。
黒点●は比較のため、おおぎ形外の点を描いたが、実際の入試では時間の節約のため描かなくてもよい。（総数が６×６＝36通り）とわかっていればよい。

また、図を描かなくても以下のような発想でも計算できる。

さいころの目のうち（5,●）（●,5)（6,●）（●,6)は半径５の円の外にあることはすぐわかるし、
（4,4)も計算すると4²＋4²＝16+16=32>25=5²

で円の外とわかる。すると(4,3)(3,4)が最大で、円周上であり、ｘ座標かｙ座標がそれ以下となると円周上あるいは円内となることがわかる。
（1,1)(1,2)(1,3)(1,4)
(2,1)(2,2)(2,3)(2,4)
(3,1)(3,2)(3,3)(3,4)
(4,1)(4,2)(4,3)
の15通りである。

座標の中でｘ座標、ｙ座標ともに整数である点を格子点（こうしてん）といい、高校入試の問題ではあれ程度の頻度で出題されるので、この問題でイメージに慣れておこう。（この図では格子点の座標は正の整数のみである。ただ、格子点のx座標、ｙ座標は正の整数とは限らず、他の問題では負の整数や０であるx座標、ｙ座標の格子点も含む出題もある。）