2016年前期、千葉県公立高校入試「数学」第3問（二次関数）解答・解説

解説
（1）

図の中で計算も示したようにAの座標は（－2,2)、Bの座標は（4,8)である。

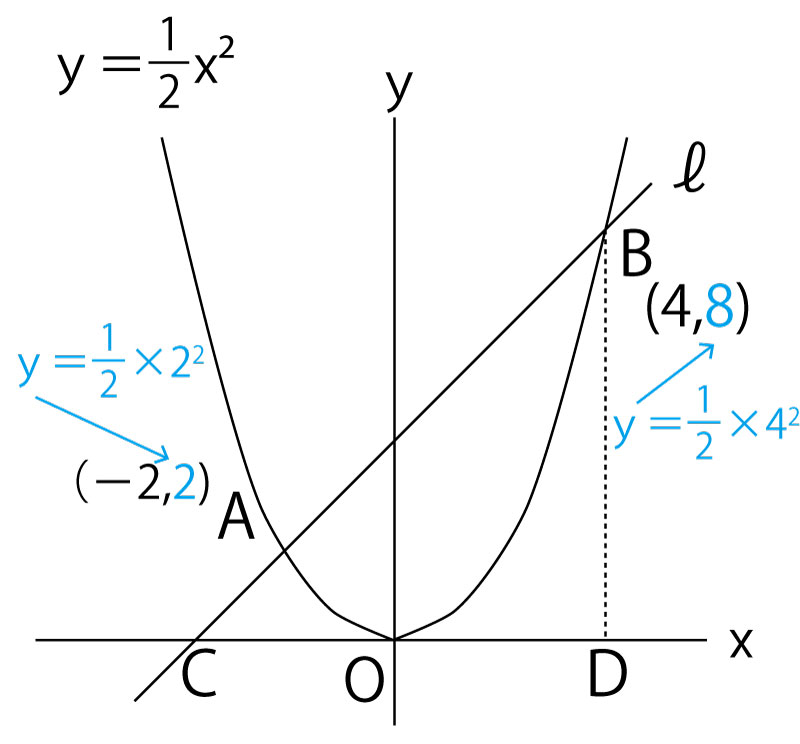
直線ℓをｙ＝ax＋bとすると、これが（－2,2)（4,8)を通るので、
２＝－2a+b・・・
8=4a＋b・・・

−より
６＝6a  a=1　これをに代入して
２＝－２×１＋ｂ　ｂ＝４
y=x+4

（2）解説

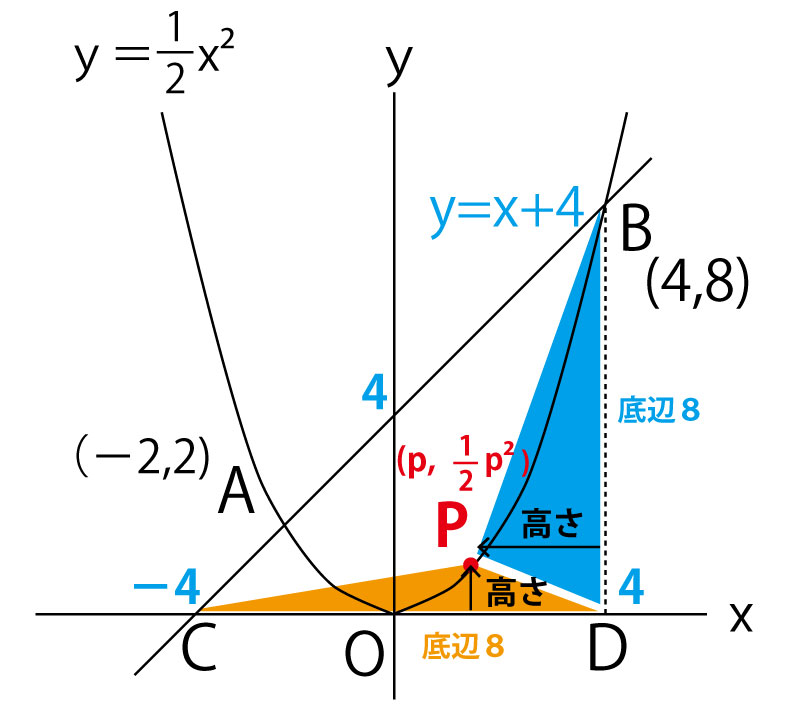
比例式の計算は以下で確認しておこう。

先の比例式を計算していくと、ｐに関する二次方程式となり、これを二次方程式の解の公式を使うとｐ（点Pのｘ座標）を求めることができる。

二次方程式の解の公式を確認しておこう。

（2）解説
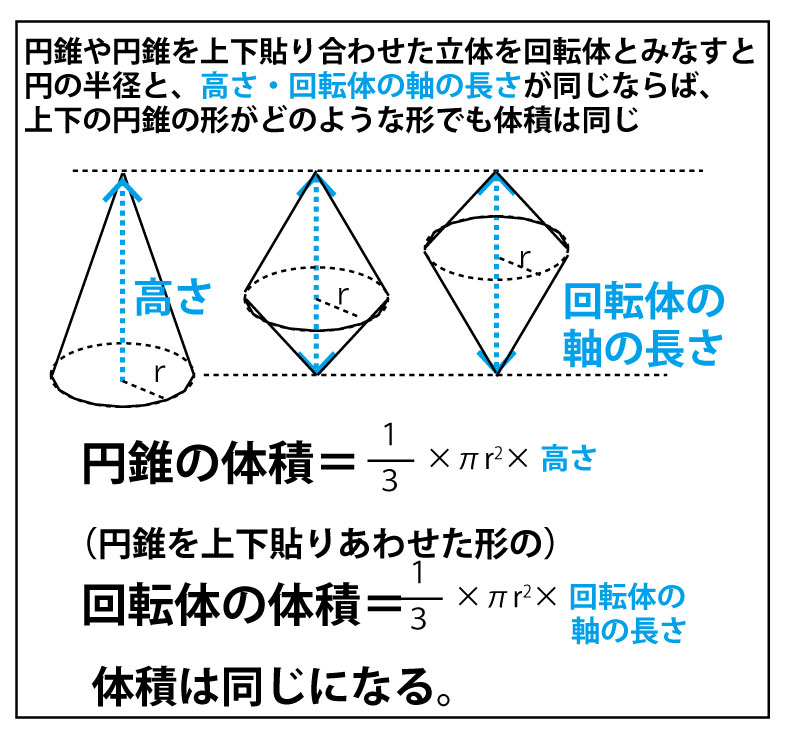
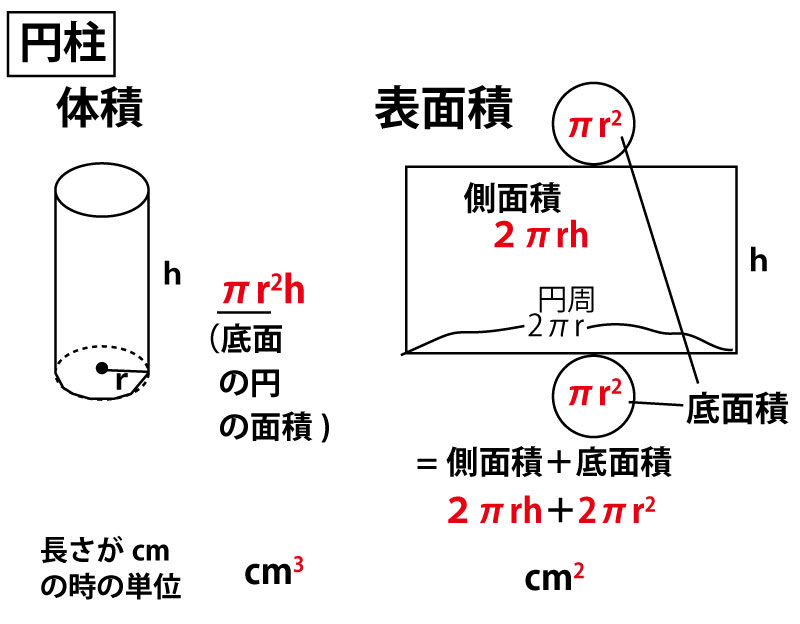
まず典型的な回転体でもある円柱と円錐の体積と表面積の基本を確認しておこう。

それでは、本問題を考えていこう。回転体の回転する図形は以下の灰色の三角形である。

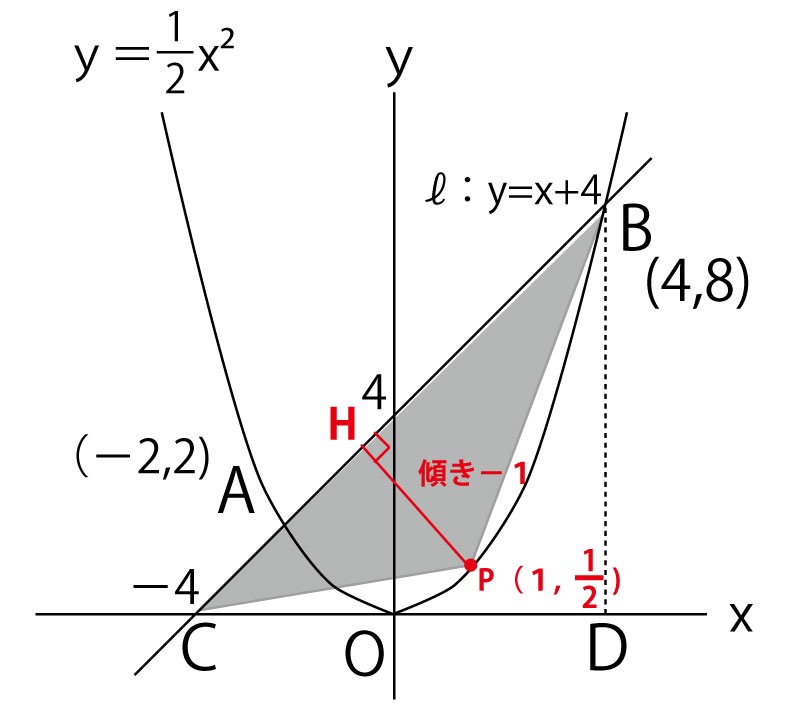
上記の計算から以下の特徴がわかるので、知っておこう。

図の中にも書き込んである通り、
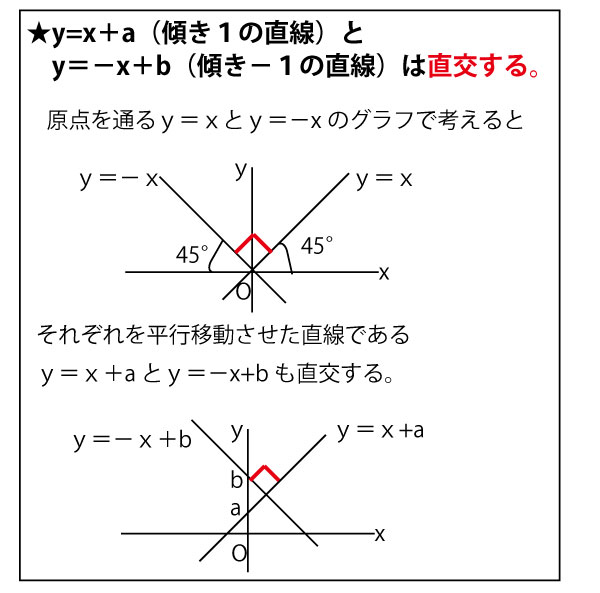
赤線で示したBHは傾き１の直線ℓと垂直なので、傾きは−１である。
このことは以下で確認しておこう。

このことを活用して、Hの座標を求める。

さらに、これからｘ軸・ｙ軸それぞれと45°の傾きを持つ傾き１、傾き−１の直線が交差する座標では、直角二等辺三角形の長さの比を知っておくと計算が便利になるので知っておこう。

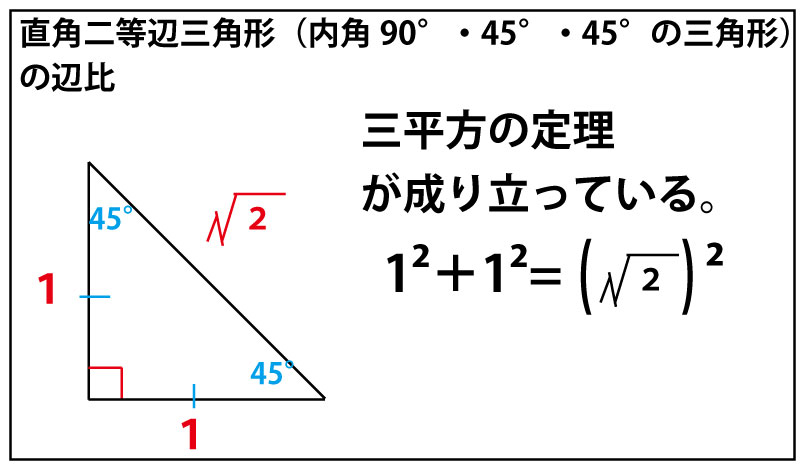
以上を前提知識として持っておくと以下の計算の発想が容易になる。

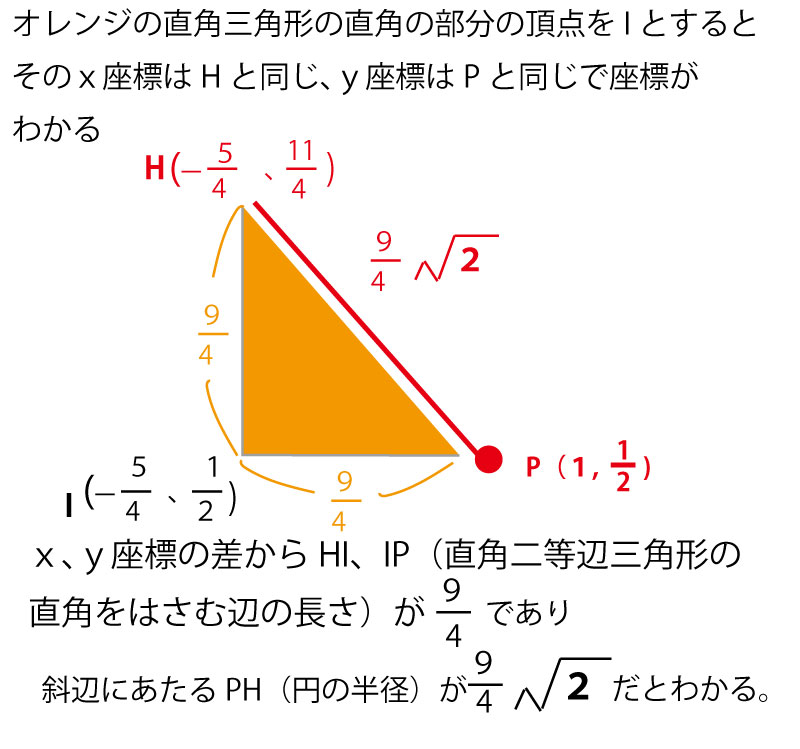
まず、上記図の青の直角二等辺三角形の辺比より、回転体の軸BCの長さがわかる。
そしてこの図のオレンジの直角三角形を考えると、回転体内の円の半径PHがわかる。
このオレンジの部分を拡大してみよう。

千葉県の場合、解答用紙に出題者がcm³を印刷してくれてあるので、単位忘れで減点となることはない。しかし入試によっては単位が書いてなく、書き忘れた場合は減点されることもともあるので注意しよう。