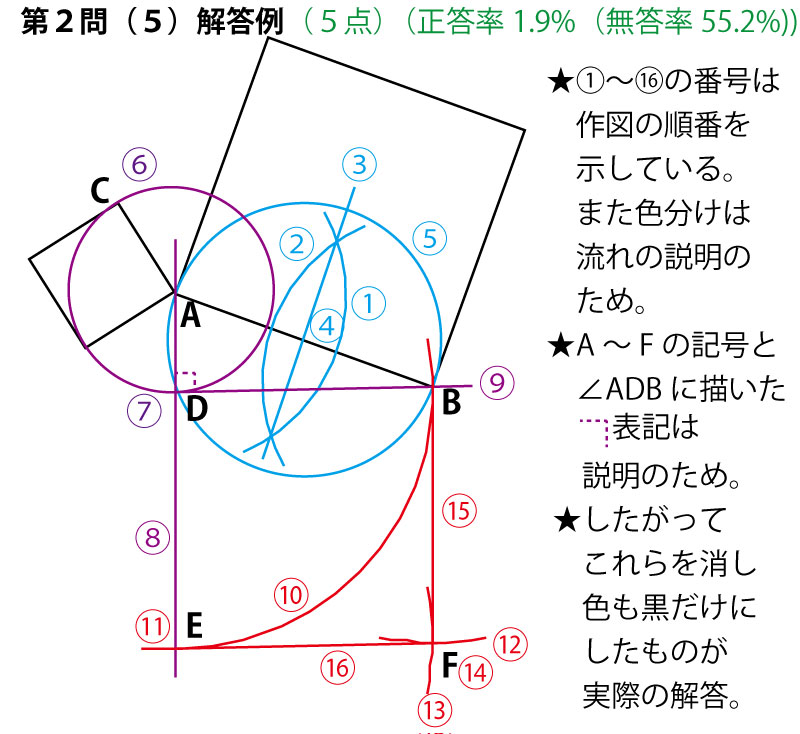
2015年前期、千葉県公立高校入試「数学」第2問（5）（作図）解答・解説

【解説】
設問が「面積が、２つの正方形の面積の差に等しい正方形」となっており、正方形の面積に注目しているので、三平方の定理が三平方の面積の関係であることをまず思い出す。

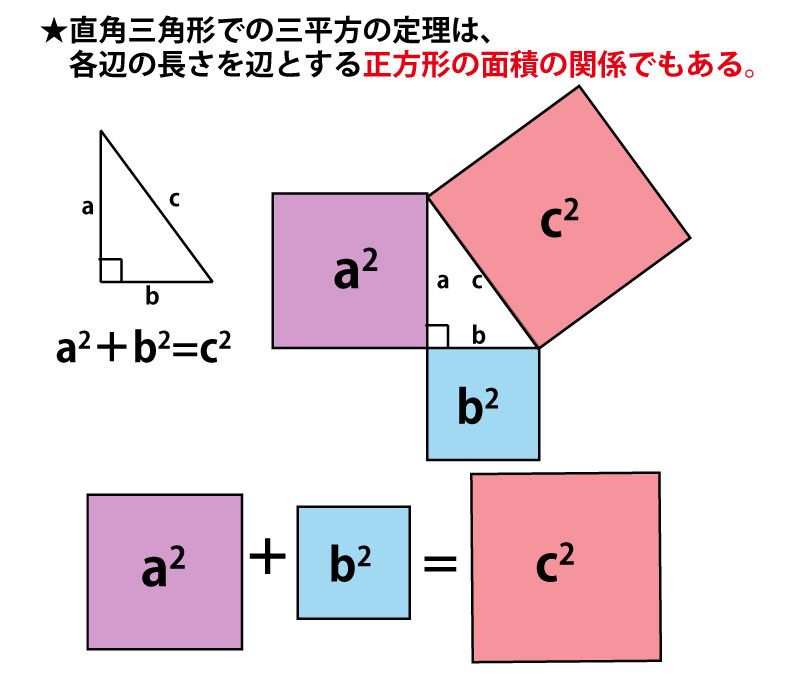
この三平方の定理を発見したピタゴラスは、広場の正方形の敷石の数を見て、この図のように発想し、この定理を思いついたという説もある。
この問題では「２つの正方形の面積の差」となっているので発想を変えてみる。

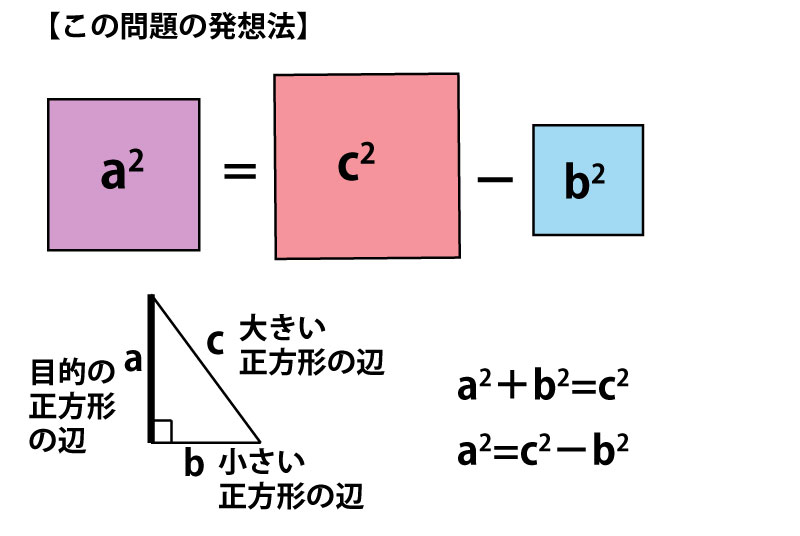
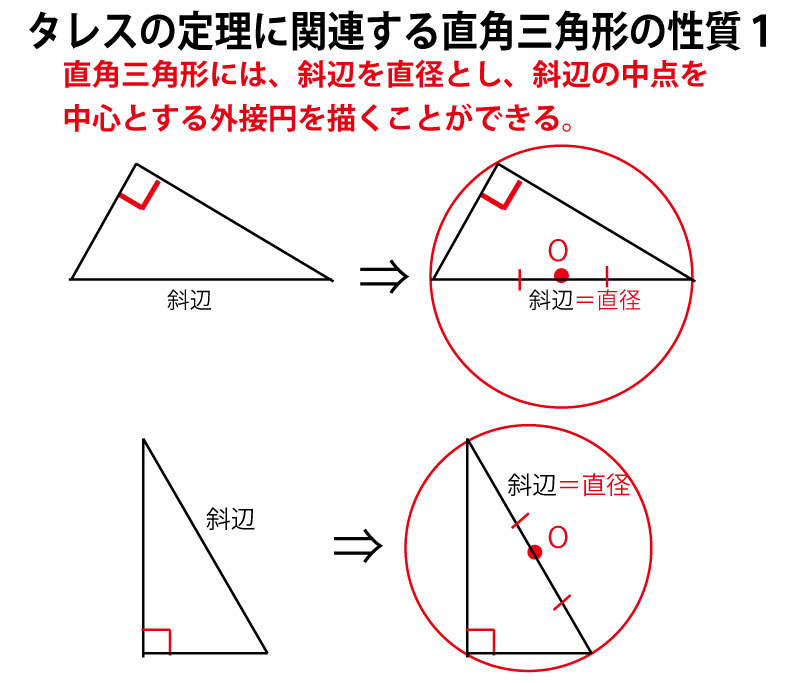
大きい正方形の辺の長さを斜辺とし、小さい正方形の直角を含む１辺の長さとする直角三角形を作図できれば、もう1辺が求めるべき正方形の辺の長さとなる。ここでコンパスの作図では円を描くことができることを考え、直角三角形と円の関係でもあるタレスの定理の活用を考える。

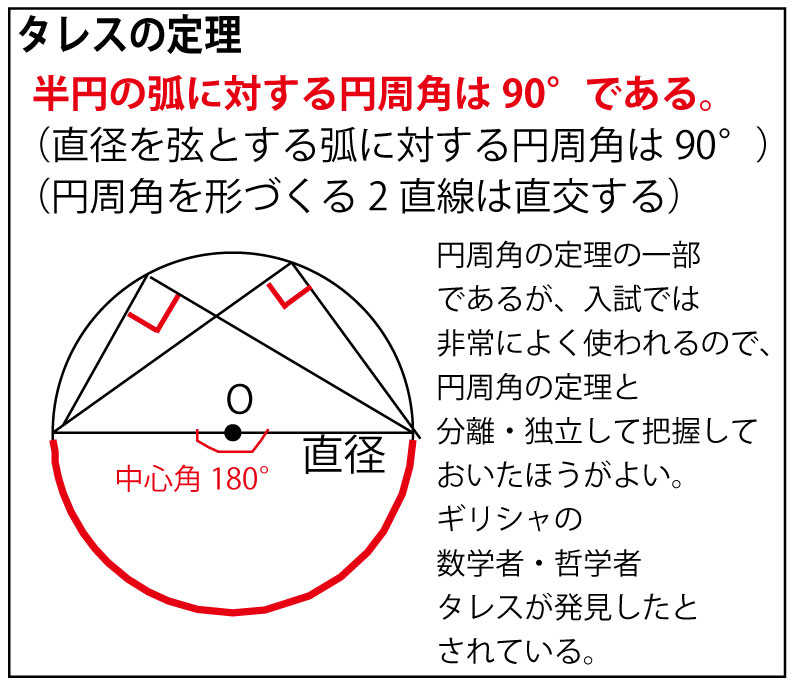
そこでまず、大きい三角形の1辺を斜辺とする円を描き、次にその辺の端の頂点から、小さい正方形の辺の長さと同じ長さとなる円周上の点を見つけ、その点ともう一つの端の頂点を結ぶと直角三角形を描くことができる。すると、それが、求めるべき正方形の1辺の長さとなる。正方形の辺の長さが求まれば、直角の角度と、その長さで幅をとったコンパスでの作図を連続的に行うと、目的の正方形が描ける。
この流れを理解して解答解説の３色で色わけした作図の流れを理解してほしい。