2021年、千葉県公立高校入試「数学」第2問（5）（作図・配点5点）問題・解答・解説
asakura
【解答】（配点5点、正答率39.2％（無答率18.4%))
番号は作図の順番であり、実際の解答用紙には要求されない（解答で要求されるのはそれぞれの線や弧を消さずに残すことである）
【解説】
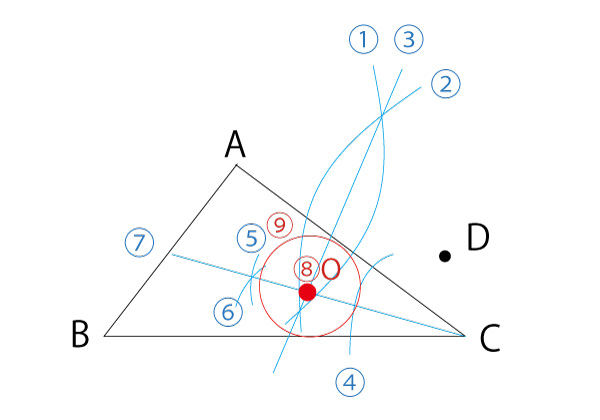
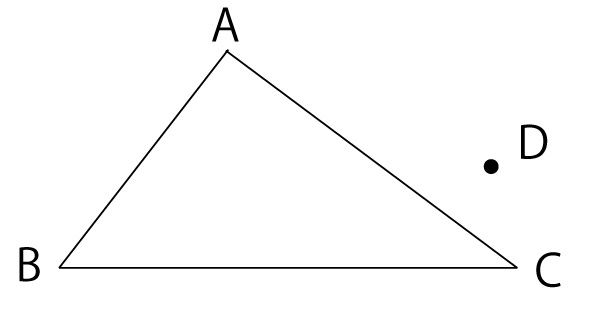
条件「・円の中心Oは、2点A、Dから等しい距離にある。」は、円Oの中心が、線分ADの垂直二等分線上にあることを示す。（詳しくは下のまとめ「作図の基礎知識」参照）
したがって、まず、線分ADの垂直二等分線を描く。
点Aを中心として、適当な幅（半径）でコンパスを開き、弧を描く。
点Dを中心として、
と同じままの幅（半径）で、弧を描く。
、
で描いた弧の２つの交点を結ぶと、ADの垂直二等分線となる。
条件「・辺ＡＣ、ＢＣは、ともに円Ｏに接する。」ということは、中心Oが∠C（∠ACB）の二等分線上にあることを示す。（詳しくは下のまとめ「作図の基礎知識」の最後の項目参照）
したがって、∠Cの二等分線を描く。
点Cを中心として、適当な幅（半径）でコンパスを開き、弧を描く。
、の弧とACとの交点を中心として、ある幅（の幅のままとするのがよい）で弧を描く。
、の弧とBCの交点を中心として、と同じ幅で弧を描く。
、点Cと の交点を結ぶと、∠C（∠ACB）の二等分線となる。
、
との交点が２つの条件を同時に満たす点であり、円Oの中心Oとなる。
Oを中心とし、AC、BCに接する幅（半径）で円を描く。
作図の基礎知識
どの年の問題での出題されていることが多い３種類の作図
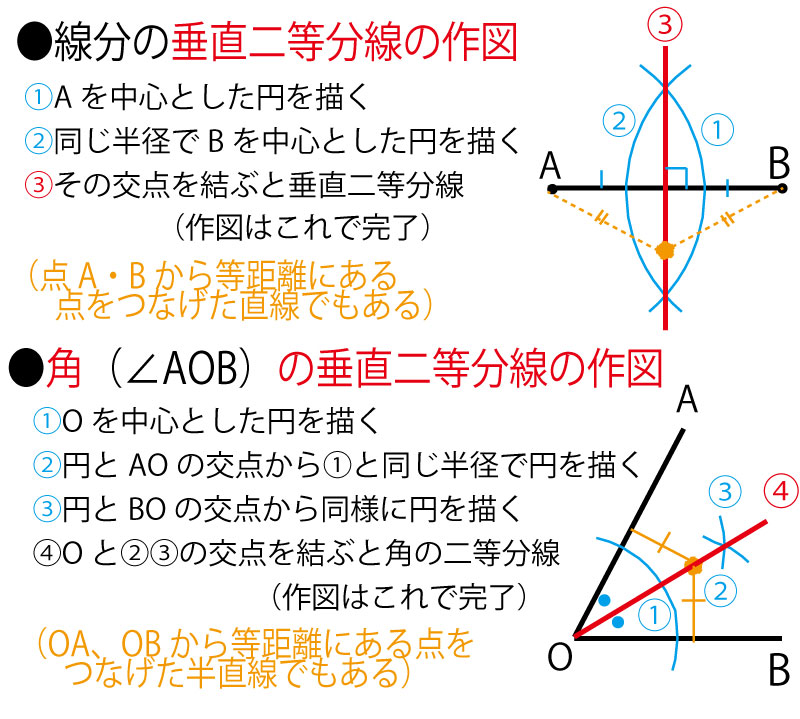
千葉県公立高校入試、第2問（5）の作図の問題では、作図に関わる様々な手法や知識が問われるが、一番使われる作図法は「垂直二等分線」と「角の二等分線」の作図である。どの年の問題でもこの２つのうちどちらかがを使う作図が出題されていると考えてほぼ間違いない。作図法を確認しておこう。
なお上記で垂直二等分線の作図①②、角の二等分線の作図①で弧を続けずに、コンパスをいったん紙から離し各直線のそばだけ作図する（弧を分離して作図する）方法でもよい。
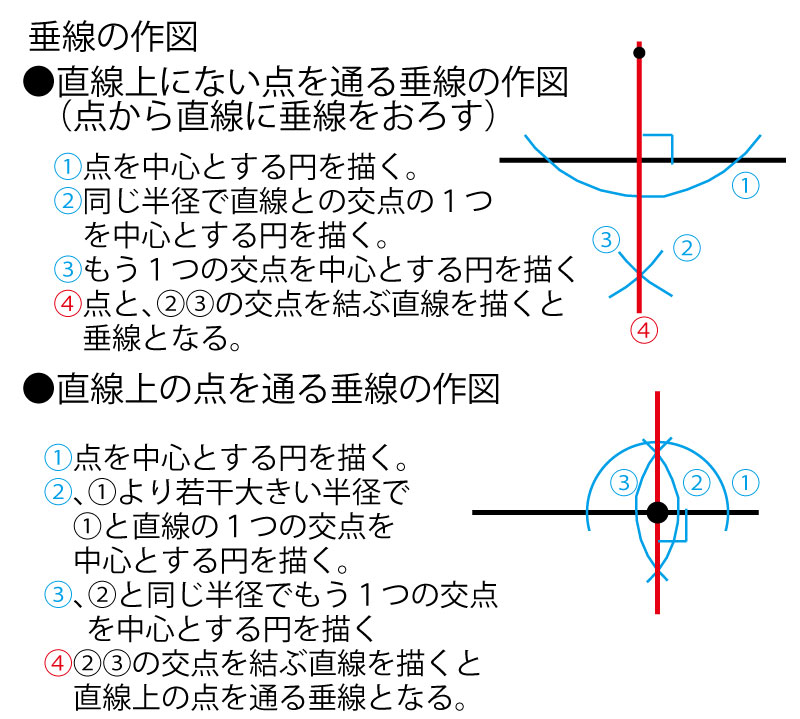
★次によくつかわれるのは垂線に関する作図である。作図法を確認しておこう。
なお上記「直線上にない点を通る垂線の作図」①、「直線上の点を通る作図」①②③で弧を続けずに、コンパスをいったん紙から離し各直線のそばだけ作図する（弧を分離して作図する）方法でもよい。
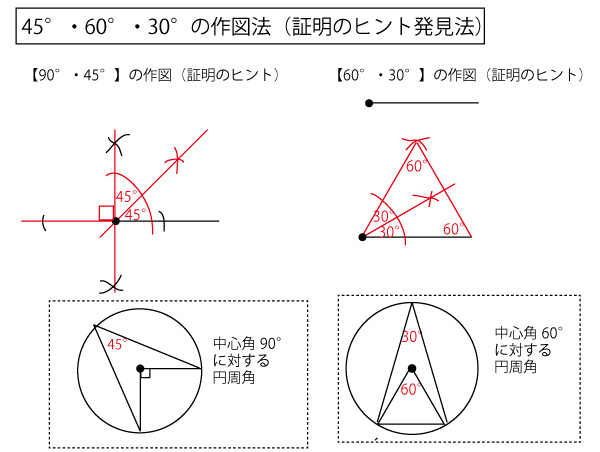
★垂線の作図と正三角形の作図ののち角の二等分線を使うと、45°・60°・30°の作図ができる。
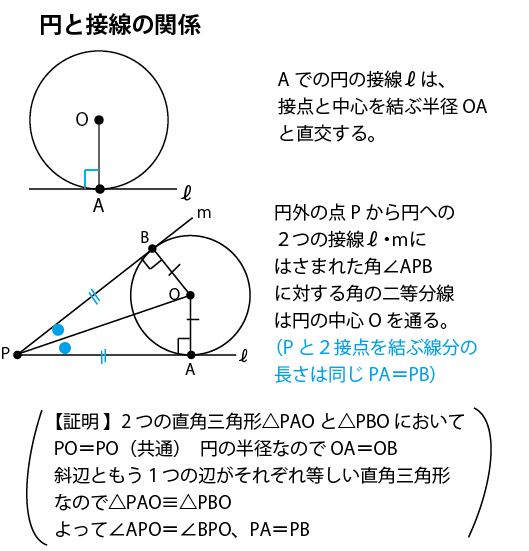
これは図形の証明の問題を解くヒントになることがあります。また中心角と円周角の関係を使うと、90°・60°中心角から、45°・30°円周角を描けます。
★円と接線との関係
作図の方針を考えていくためには、小中学校で学んだ三角形・四角形・円・角度などに関する様々な性質を知っておく必要がある。円と接線の関係を確認しておこう。
